
全程设计 第2课时 积化和差与和差化积公式
第2课时 积化和差与和差化积公式

导航 课标定位素养阐释 L.能根据公式Sn和Ca知推导出积化和差与和差化积公式 2.了解三角变换在解决有关数学问题中所起的作用,进一步体 会三角变换的特点. 3.提高逻辑推理能力和数学运算能力
导航 课标定位 素养阐释 1.能根据公式Sα±β和Cα±β推导出积化和差与和差化积公式. 2.了解三角变换在解决有关数学问题中所起的作用,进一步体 会三角变换的特点. 3.提高逻辑推理能力和数学运算能力
课前·基础认知 课堂·重难突破 随堂训练 规范解答
规 范 解 答 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 积化和差公式 【问题思考】 l.在公式sin(a+p)=sin acos B-+cos asin B和sin(a-p)=sin acos B- cos asin Br中,能否用sin(a+p)和sin(a-P)表示sin acos B,cos asin ? 提示:能.将sin acos B和cos asin B看作未知数,解方程组可得
导航 课前·基础认知 一、积化和差公式 【问题思考】 1.在公式sin(α+β)=sin αcos β+cos αsin β和sin(α-β)=sin αcos β- cos αsin β中,能否用sin(α+β)和sin(α-β)表示sin αcos β,cos αsin β? 提示:能.将sin αcos β和cos αsin β看作未知数,解方程组可得

导航 2.积化和差公式: cos acos B= ● sin asin B- sin acos B- cos asin B=
导航 2.积化和差公式: cos αcos β= 𝟏 𝟐 [cos(α+β)+cos(α-β)] ; sin αsin β= - 𝟏 𝟐 [cos(α+β)-cos(α-β)] ; sin αcos β= 𝟏 𝟐 [sin(α+β)+sin(α-β)] ; cos αsin β= 𝟏 𝟐 [sin(α+β)-sin(α-β)]
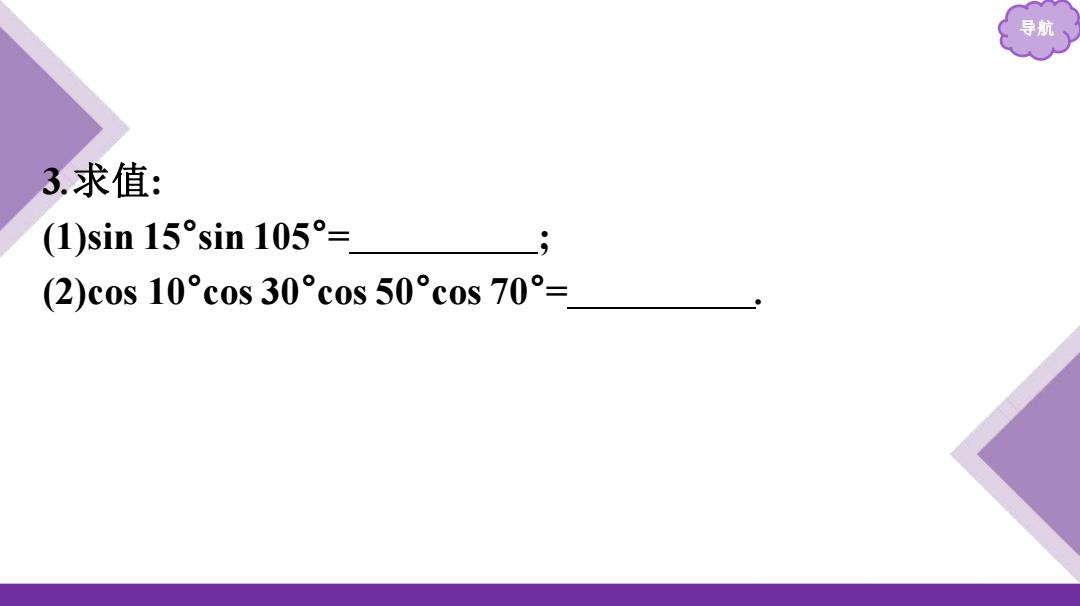
导航、 3.求值: (1)sin15°sin105°= (2)c0s10°c0s30°c0s50°c0s70°=
导航 3.求值: (1)sin 15°sin 105° = ; (2)cos 10°cos 30°cos 50°cos 70° =

解析:()原式=21c0s(15°+105°c0s(15°-10s°)子 导 2)c0s10°c0s30°c0s50°c0s70° cs10°×9×0s50+70°H0s150°-70°1 7s10(3+cos20°)片cs10:os106c0s20 c0s10°+3×cos(10°+20°)+c0s(10°-20) 8 8 10° 2+c0s10°) cos 10° 8 + 8c0s10°=3 6 答案:(1 (2)
解析 导航 :(1)原式=- 𝟏 𝟐 [cos(15°+105°)-cos(15°-105°)]= 𝟏 𝟒 . (2)cos 10°cos 30°cos 50°cos 70° =cos 10°× 𝟑 𝟐 × 𝟏 𝟐 [cos(50°+70°)+cos(50°-70°)] = 𝟑 𝟒 cos 10° - 𝟏 𝟐 + 𝐜𝐨𝐬𝟐𝟎° =- 𝟑 𝟖 cos 10°+ 𝟑 𝟒 cos 10°cos 20° =- 𝟑 𝟖 cos 10°+ 𝟑 𝟒 × 𝟏 𝟐 [cos(10°+20°)+cos(10°-20°)] =- 𝟑 𝟖 cos 10°+ 𝟑 𝟖 𝟑 𝟐 + 𝐜𝐨𝐬𝟏𝟎° =- 𝟑 𝟖 cos 10°+ 𝟑 𝟏𝟔 + 𝟑 𝟖 cos 10°= 𝟑 𝟏𝟔 . 答案:(1)𝟏 𝟒 (2) 𝟑 𝟏𝟔

导航 二、和差化积公式 【问题思考】 1.借助于积化和差公式,我们可以把正弦、余弦的积的形式化 为正弦或余弦的和或差的形式,那么已知正弦或余弦的和或 差的形式,能否化为正弦或余弦的积的形式? 提示:对于Acos+Bcosy:或Asinx+Bsin,只要A=B,就可以化 为积的形式
导航 二、和差化积公式 【问题思考】 1.借助于积化和差公式,我们可以把正弦、余弦的积的形式化 为正弦或余弦的和或差的形式,那么已知正弦或余弦的和或 差的形式,能否化为正弦或余弦的积的形式? 提示:对于Acos x+Bcos y或Asin x+Bsin y,只要A=B,就可以化 为积的形式

导航 2.和差化积公式: cos x+cos= COS x-COS sin x+sin y= sin x-siny=
导航 2.和差化积公式: cos x+cos y= 2cos 𝒙+𝒚 𝟐 cos 𝒙-𝒚 𝟐 ; cos x-cos y= -2sin 𝒙+𝒚 𝟐 sin 𝒙-𝒚 𝟐 ; sin x+sin y= 2sin 𝒙+𝒚 𝟐 cos 𝒙-𝒚 𝟐 ; sin x-sin y= 2cos 𝒙+𝒚 𝟐 sin 𝒙-𝒚 𝟐

导航、 3.求下列各式的值: (1)sin54°-sin18°; (2)C0s146°+c0s94°+2c0s47°c0s73°
导航 3.求下列各式的值: (1)sin 54°-sin 18° ; (2)cos 146°+cos 94°+2cos 47°cos 73°