
全程设计 7.3.2 正弦型屡数的性质与图象
7.3.2 正弦型函数的性质与图象

导航 课标定位 素养阐释 1.了解正弦型函数y=Asin(wx+p)A≠0,w≠0)的定义及性质. 2.能求正弦型函数的周期、最值、单调区间等. 3.会用“图象变换法”作正弦型函数y=Asin(wx十p)的图象. 4.加强数学运算、直观想象和逻辑推理能力的培养
导航 课标定位 素养阐释 1.了解正弦型函数y=Asin(ωx+φ)(A≠0,ω≠0)的定义及性质. 2.能求正弦型函数的周期、最值、单调区间等. 3.会用“图象变换法”作正弦型函数y=Asin(ωx+φ)的图象. 4.加强数学运算、直观想象和逻辑推理能力的培养
课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 正弦型函数 【问题思考】 1.函数-2sin(行x+)的定义域、值域、周期是什么? 提示:R;-2,26π
导航 课前·基础认知 一、正弦型函数 【问题思考】 1.函数 y=2sin 的定义域、值域、周期是什么? 𝟏 𝟑 𝒙 + 𝛑 𝟒 提示:R;[-2,2];6π

导航 2.填空: ()一般地,形如 (其中A,ω,0都是常数,且 A0,ω≠0)的函数,通常叫做正弦型函数 (2)一般地,正弦型函数y=Asin(wx+p)(其中A0,0≠0,x∈R)的 周期1需频率∫品初相为_,值域为 也称为振 幅,A的大小反映了y=Asin(ox+p)的波动幅度的大小
导航 2.填空: (1)一般地,形如y=Asin(ωx+φ) (其中A,ω,φ都是常数,且 A≠0,ω≠0)的函数,通常叫做正弦型函数. (2)一般地,正弦型函数 y=Asin(ωx+φ)(其中 A≠0,ω≠0,x∈R)的 周期 T=𝟐𝛑 |𝝎| ,频率 f=|𝝎| 𝟐𝛑 ,初相为 φ,值域为[-|A|,|A|],|A|也称为振 幅,|A|的大小反映了 y=Asin(ωx+φ)的波动幅度的大小

导航 3.做一做:已知函数)=4sin(4x+羽),则函数的最小正周期 是 ;振幅是 ;初相是 答案 4开
导航 3.做一做:已知函数 y=4sin 𝟒𝒙 + 𝛑 𝟒 ,则函数的最小正周期 是 ;振幅是 ;初相是 . 答案: 𝛑 𝟐 4 𝛑 𝟒

导 二、A,0,0对函数y=Asin(wx+p)图象的影响 【问题思考】 1如何由y-sinx的图象得到sin=sin2c一sin(x-君))的 图像? 提示y=inx图象上各,点的横坐标不变,纵坐标变为原来的,得 到2sinx的图象=sinx图象上各点的蚁坐标不变,横坐标变 为原来的,得到y=sin2x的图象;=sinx的图象向右平移需个单 位,得到=sinc的图象
导航 二、A,ω,φ对函数y=Asin(ωx+φ)图象的影响 【问题思考】 1.如何由 y=sin x 的图象得到 y=𝟏𝟐 sin x,y=sin 2 x,y=sin 𝒙- 𝛑𝟔 的 图像 ? 提示:y=sin x 图 象上各点的横坐标不变,纵坐标变为原来的 𝟏𝟐,得 到 y= 𝟏𝟐 sin x 的图 象;y=sin x 图 象上各点的纵坐标不变,横坐标变 为原来的 𝟏𝟐,得到 y=sin 2 x 的图 象;y=sin x 的图 象向右平移 𝛑𝟔 个单 位,得到 y=sin(x-𝛑𝟔)的图 象
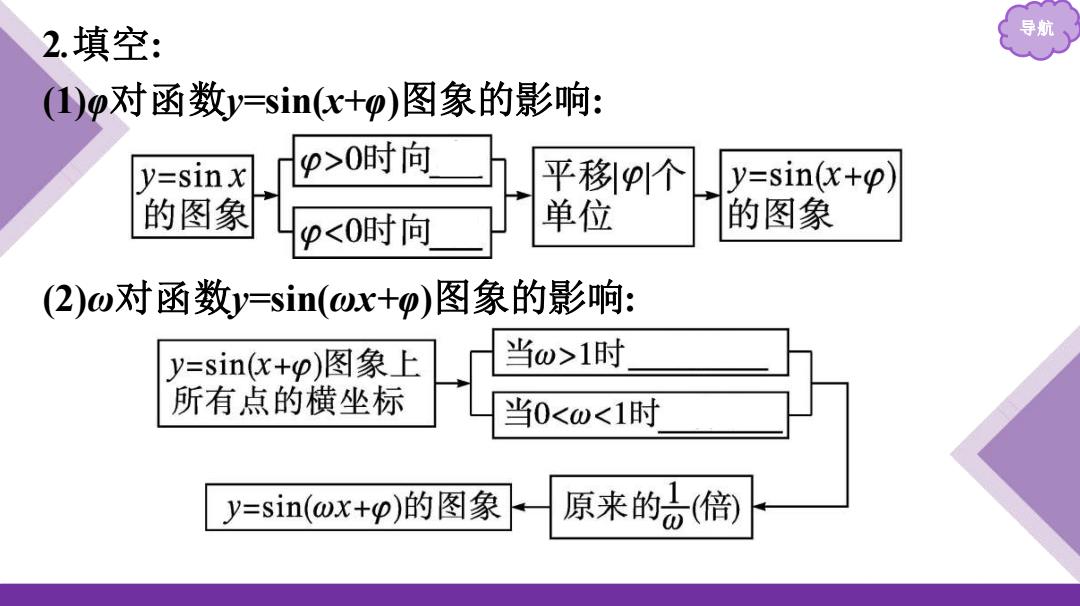
2.填空: 导航 ()p对函数y=sin(x+p)图象的影响: y=sinx p>0时问 平移p个 y=sin(x+p) 的图象 p1时 所有点的横坐标 当0<w<1时 y=sin(wx+p)的图象 原来的。倍)
导航 2.填空: (1)φ对函数y=sin(x+φ)图象的影响: (2)ω对函数y=sin(ωx+φ)图象的影响:
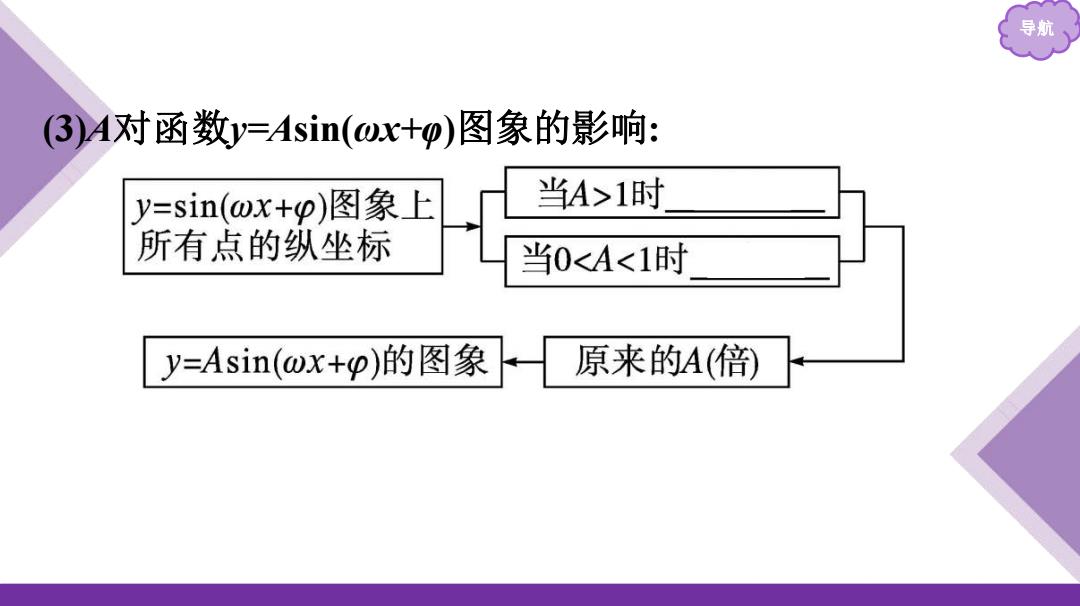
导航 (3)A对函数y=Asin(wx+p)图象的影响: y=sin(wx+p)图象上 当A>1时 所有点的纵坐标 当0<A<1时 y=Asin(wx+p)的图象 原来的A(倍)
导航 (3)A对函数y=Asin(ωx+φ)图象的影响:

导航 〔4)用“变换法”作图: 向(o>0)或向:(p<0) y=sinx的图象 平移|个单位 y=sin(x+p)的图象 横坐标变为原来的 倍 纵坐标不变 y=sin(wx+p)的图象 纵坐标变为原来的倍 横坐标不变 y=Asin(wx+p)的图象
导航 (4) 用 “变换法 ”作图: y=sin x 的图象 y=sin(x+ φ)的图象 y=sin( ωx+ φ)的图象 y=Asin( ωx+ φ)的图象