
全程设计 7.2.2 单位圆与三角函数线
7.2.2 单位圆与三角函数线

导航、 课标定位素养阐释 1.了解三角函数线的意义. 2.会用三角函数线表示一个角的正弦、余弦和正切 3.加强直观想象和逻辑推理能力的培养
导航 课标定位 素养阐释 1.了解三角函数线的意义. 2.会用三角函数线表示一个角的正弦、余弦和正切. 3.加强直观想象和逻辑推理能力的培养
课前·基础认知 课堂·重难突破 随堂训练 思想方法
思 想 方 法 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 三角函数线 【问题思考】 1.正弦值、余弦值、正切值因角α的不同,可能为正值、可能 为负值,也可能为0.而有向线段既有大小又有方向,能否用有 向线段表示sina,cosa,tana? 提示:能有向线段的方向与三角函数值的正负吻合,长度与三 角函数值的绝对值的大小对应
导航 课前·基础认知 三角函数线 【问题思考】 1.正弦值、余弦值、正切值因角α的不同,可能为正值、可能 为负值,也可能为0.而有向线段既有大小又有方向,能否用有 向线段表示sin α,cos α,tan α? 提示:能.有向线段的方向与三角函数值的正负吻合,长度与三 角函数值的绝对值的大小对应

导 2填空:(1)一般地,在平面直角坐标系中,坐标满足 的 点组成的集合称为单位圆若角a的终边与单位圆的交点为P, 则点P的坐标为 (2)如果过角α的终边与单位圆的交点P作x轴的垂线,垂足 为M,过点A(1,0)作与x轴垂直的直线L,与角a的终边(或其反 向延长线)交于点T,那么角a的正弦线是MP,余弦线为0M, 正切线为AT.正弦线、余弦线和正切线都称为三角函数线
导航 2.填空:(1)一般地,在平面直角坐标系中,坐标满足 x 2+y2=1 的 点组成的集合称为单位圆.若角α的终边与单位圆的交点为P, 则点P的坐标为 (cos α,sin α) . (2)如果过角 α 的终边与单位圆的交点 P 作 x 轴的垂线,垂足 为 M,过点 A(1,0)作与 x 轴垂直的直线 l,与角 α 的终边(或其反 向延长线)交于点 T,那么角 α 的正弦线是𝑴 𝑷 ,余弦线为𝑶 𝑴 , 正切线为𝑨 𝑻 .正弦线、余弦线和正切线都称为三角函数线
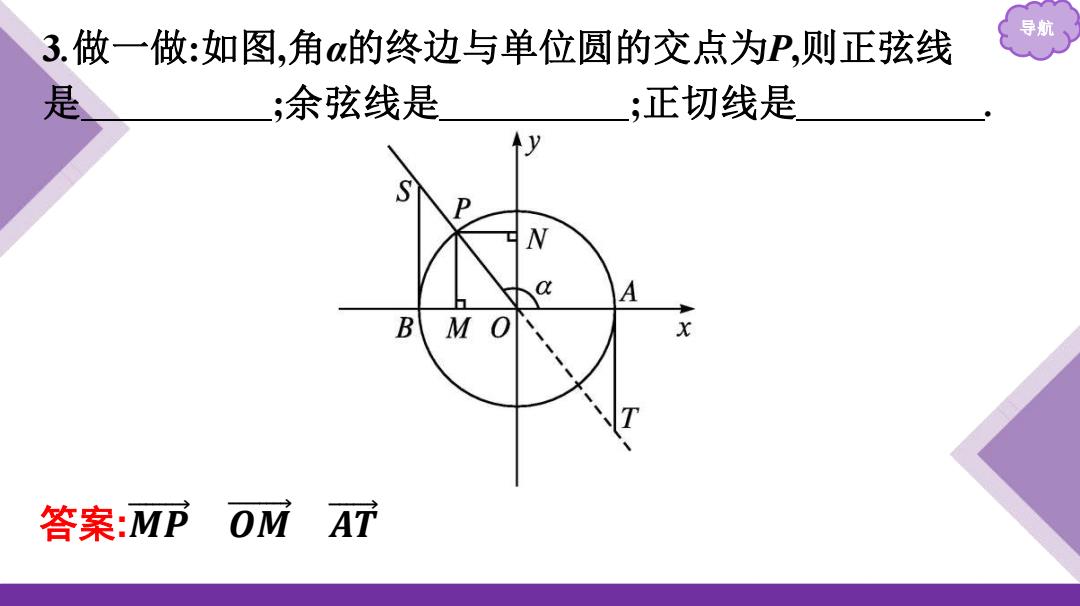
3.做一做:如图,角a的终边与单位圆的交点为P,则正弦线 导航 是 ;余弦线是 ;正切线是 B M 答案:MPOM A7
导航 3.做一做:如图,角α的终边与单位圆的交点为P,则正弦线 是 ;余弦线是 ;正切线是 . 答案:𝑴 𝑷 𝑶 𝑴 𝑨 𝑻

导 思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X”. (1)三角函数线的长度等于三角函数值.() (2)三角函数线的方向表示三角函数值的正负.( (3)对任意角都能作出正弦线、余弦线和正切线( (④)没有正切线.()
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)三角函数线的长度等于三角函数值.( × ) (2)三角函数线的方向表示三角函数值的正负.( √ ) (3)对任意角都能作出正弦线、余弦线和正切线.( × ) (4) 没有正切线.( × ) 𝟓𝛑 𝟒

导航 课堂·重难突破 探究一作已知角的三角函数线 【例1】作出3的正弦线、余弦线和正切线,并利用三角函数 线求sin平cos平tan的值
导航 课堂·重难突破 探究一 作已知角的三角函数线 【例 1】 作出𝟑𝛑 𝟒 的正弦线、余弦线和正切线,并利用三角函数 线求 sin 𝟑𝛑 𝟒 ,cos 𝟑𝛑 𝟒 ,tan 𝟑𝛑 𝟒 的值

解:在直角坐标系中作单位圆,如图,以0x轴为抬边作买角,角 的 导 终边与单位圆交于点P,作PM⊥x轴,垂足为M,由单位圆与x轴 正方向的交点A作x轴的垂线,与OP的反向延长线交于点T,即 3亚的正弦线为M亚,余弦线为0M,正切线为AT. 在Rt△OMP和Rt△OAT中,易知OM=MP-AIT=l, 故sin 3 M
导航 解:在直角坐标系中作单位圆,如图,以 Ox 轴为始边作𝟑𝛑 𝟒 角,角的 终边与单位圆交于点 P,作 PM⊥x 轴,垂足为 M,由单位圆与 x 轴 正方向的交点 A 作 x 轴的垂线,与 OP 的反向延长线交于点 T,即 𝟑𝛑 𝟒 的正弦线为𝑴 𝑷 ,余弦线为𝑶 𝑴 ,正切线为𝑨 𝑻 . 在 Rt△OMP 和 Rt△OAT 中,易知|OM|=|MP|= 𝟐 𝟐 ,|AT|=1, 故 sin 𝟑𝛑 𝟒 = 𝟐 𝟐 ,cos 𝟑𝛑 𝟒 =- 𝟐 𝟐 ,tan 𝟑𝛑 𝟒 =-1

了延伸探究 当a∈(侵,),且a逐渐增大时,sina,cosa,tana的值如何变化? 解:sina从1变到0;c0sa由0变到-1;tana由-oo变到0.(取不到端 点值) 反思感悟 作已知角的三角函数线时,先确定角α终边的位置,再画线.同 时应注意所画线的方向
导航 当 α∈ ,且α逐渐增大时,sin α,cos α,tan α的值如何变化? 𝛑 𝟐 ,𝛑 解:sin α从1变到0;cos α由0变到-1;tan α由-∞变到0.(取不到端 点值) 反思感悟 作已知角的三角函数线时,先确定角α终边的位置,再画线.同 时应注意所画线的方向