
全程设计 3.1.1 国数及其表示方法 第4课时 分段国数及其应用
3.1.1 函数及其表示方法 第4课时 分段函数及其应用
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解分段函数的概念. 2.会用解析法及图象法表示分段函数 3.根据分段函数能研究有关性质
导航 课标定位素养阐释 1.了解分段函数的概念. 2.会用解析法及图象法表示分段函数. 3.根据分段函数能研究有关性质

导航 课前·基础认知 分段函数 【问题思考】 1.阅读下面的实例并回答问题: 某市空调公共汽车的票价按下列规则制定: (1)不超过5km,票价2元; (2)5km以上,每增加5km,票价增加1元(不足5km的按5km计 算)
导航 课前·基础认知 分段函数 【问题思考】 1.阅读下面的实例并回答问题: 某市空调公共汽车的票价按下列规则制定: (1)不超过5 km,票价2元; (2)5 km以上,每增加5 km,票价增加1元(不足5 km的按5 km计 算)

已知两个相邻的公共汽车站间相距1km,沿途(包括起点站和戴 终点站)有11个汽车站. ()从起点站出发,公共汽车的行程x(单位:km)与票价y(单位: 元)有函数关系吗? (2)若有函数关系,则函数的解析式是什么? 3)x与y之间有何特点? 提示:(1)有函数关系. 2,0<x≤5, 2=3,5<x≤10. (3)当x在不同区间内取值时,与y所对应的关系不同
导航 已知两个相邻的公共汽车站间相距1 km,沿途(包括起点站和 终点站)有11个汽车站. (1)从起点站出发,公共汽车的行程x(单位:km)与票价y(单位: 元)有函数关系吗? (2)若有函数关系,则函数的解析式是什么? (3)x与y之间有何特点? 提示:(1)有函数关系. (2)y= 𝟐,𝟎 < 𝒙 ≤ 𝟓, 𝟑,𝟓 < 𝒙 ≤ 𝟏𝟎. (3)当x在不同区间内取值时,与y所对应的关系不同

2填空:如果一个函数,在其定义域内,对于自变量的不同取值航 区间,有不同的 ,则称其为分段函数 3做一做:函数gx4,0 x2+1,x≥1的定义域为 2x-1,x≥0则f2+-I- 2)已知函数)尸2-4x,x <0, 解析:)分段函数的定义域是各段自变量取值范围的并集, 所以函数fx)的定义域为(-oo,0)U[1,+oo) (2f2)+f-1)=(2×2-1)+2-4×(-1)1=9. 答案:(1)(-0,0)U[1,+∞)(2)9
导航 2.填空:如果一个函数,在其定义域内,对于自变量的不同取值 区间,有不同的对应方式,则称其为分段函数. 3.做一做:(1)函数 f(x)= 𝒙 𝟐 + 𝟏,𝒙 ≥ 𝟏, 𝟑𝒙-𝟒,𝒙 < 𝟎 的定义域为 . (2)已知函数 f(x)= 𝟐𝒙-𝟏,𝒙 ≥ 𝟎, 𝟐-𝟒𝒙,𝒙 < 𝟎, 则 f(2)+f(-1)= . 解析:(1)分段函数的定义域是各段自变量取值范围的并集, 所以函数f(x)的定义域为(-∞,0)∪[1,+∞). (2)f(2)+f(-1)=(2×2-1)+[2-4×(-1)]=9. 答案:(1)(-∞,0)∪[1,+∞) (2)9

导 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“X” (1)分段函数各段上的自变量的取值范围的并集为R(×) (2)分段函数各段上的函数值集合的交集为@.(×) (3)分段函数的图象一定是不连续的.(×)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)分段函数各段上的自变量的取值范围的并集为R.( ) (2)分段函数各段上的函数值集合的交集为⌀.( ) (3)分段函数的图象一定是不连续的.( ) × × ×

导航 课堂·重难突破 探究一分段函数求值问题 【例1】已知函数 x+1,X≤-2, fx)=x2+2x,-2<x<2, 2x-1,x≥2. )求-53)f()的值; (2)若f=3,求实数a的值
导航 课堂 ·重难突破 探究一分段函数求值问题 【例 1 】已知函数 f(x)= 𝒙 + 𝟏,𝒙 ≤ -𝟐, 𝒙𝟐 + 𝟐𝒙,-𝟐 < 𝒙 < 𝟐, 𝟐𝒙-𝟏,𝒙 ≥ 𝟐. (1) 求 f(-5),f(-√ 𝟑),f 𝒇 - 𝟓𝟐 的值; (2) 若 f(a)=3,求实数 a 的值
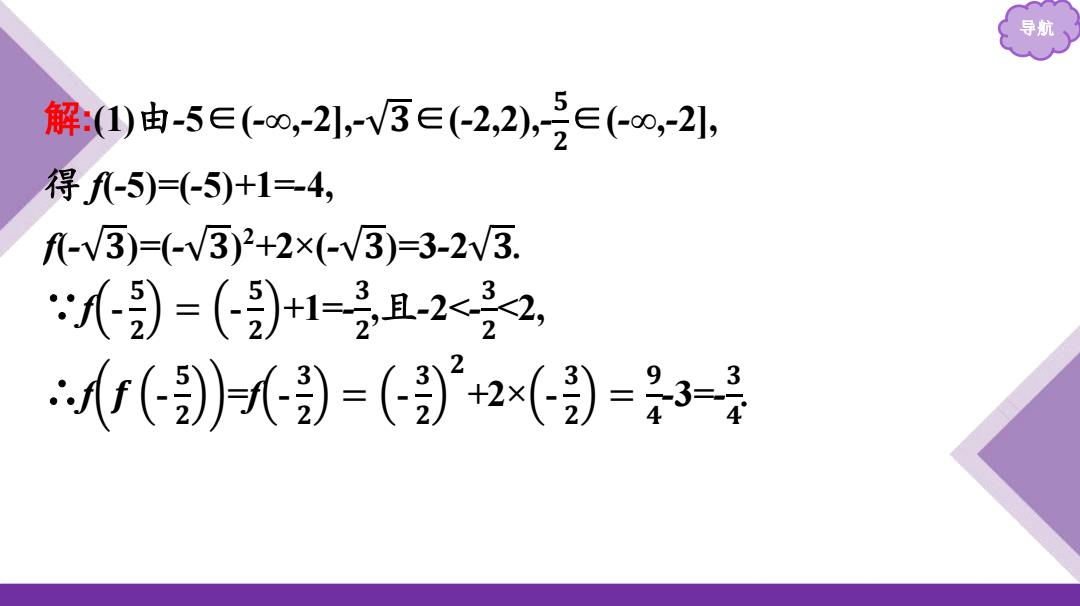
导航 解:(1)由-5∈(0,-2,-V3∈(-2,2),5∈(0,-2, 得-5)=(-5)+1=4, f-V3)=(V3)2+2×(V3)=3-2V3. “(-)=()+1=2且-2×32, f()到=(》+2x(》=3
导航 解:(1)由-5∈(-∞,-2],-√𝟑∈(-2,2),- 𝟓 𝟐 ∈(-∞,-2], 得 f(-5)=(-5)+1=-4, f(-√𝟑)=(-√𝟑) 2 +2×(-√𝟑)=3-2√𝟑. ∵f - 𝟓 𝟐 = - 𝟓 𝟐 +1=- 𝟑 𝟐 ,且-2<- 𝟑 𝟐 <2, ∴f 𝒇 - 𝟓 𝟐 =f - 𝟑 𝟐 = - 𝟑 𝟐 𝟐 +2× - 𝟑 𝟐 = 𝟗 𝟒 -3=- 𝟑 𝟒

导航 2)当≤-2时,a+1=3, 解得=2>-2,不合题意,舍去; 当-2<<2时,2+2a=3, 即2+2a-3=0. 解得=1或a=3. .1∈(-2,2),-3庄(-2,2), ∴.=1符合题意; 当≥2时,2-1=3,解得=2,符合题意. 综上可得,=1或=2
导航 (2) 当 a ≤ - 2 时 ,a+ 1 =3, 解得a= 2 >-2,不合题意 ,舍去 ; 当 - 2<a< 2 时 , a 2 + 2a=3, 即 a 2 + 2 a - 3 = 0 . 解得a= 1 或a=- 3 . ∵ 1 ∈ ( -2,2), - 3 ∉ ( -2,2), ∴a= 1符合题意 ; 当 a ≥ 2 时,2 a - 1 =3,解得a=2,符合题意 . 综上可得 ,a= 1 或a= 2