
全程设计 3.1.1 函数及其表示方法 第3课时 函数的表示方法
3.1.1 函数及其表示方法 第3课时 函数的表示方法
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解函数的表示方法 2.掌握求函数解析式的常见方法 3.掌握用描,点法作函数图象的方法
导航 课标定位素养阐释 1.了解函数的表示方法. 2.掌握求函数解析式的常见方法. 3.掌握用描点法作函数图象的方法

导航 课前·基础认知 函数的表示方法 【问题思考】 1阅读下面的实例并回答问题: 实例1某物体从高度为44.1m的空中自由下落,物体下落的 距离s(单位:m)与所用时间t(单位:s)的平方成正比,这个规律 用数学式子可以描述为s=g,其中g取9.8m/s3
导航 课前·基础认知 一、函数的表示方法 【问题思考】 1.阅读下面的实例并回答问题: 实例1 某物体从高度为44.1 m的空中自由下落,物体下落的 距离s(单位:m)与所用时间t(单位:s)的平方成正比,这个规律 用数学式子可以描述为s= gt2 ,其中g取9.8 m/s2 . 𝟏 𝟐
实例2下表是高一()班一组同学期中考试的数学成绩分数航 表 学号 5 13 14 35 36 40 分数 102 119 90 107 98 110 89 实例3 某地2018年8月8日24小时气温变化曲线如图所示 气温/C 312976523110 24681012141618202224时间
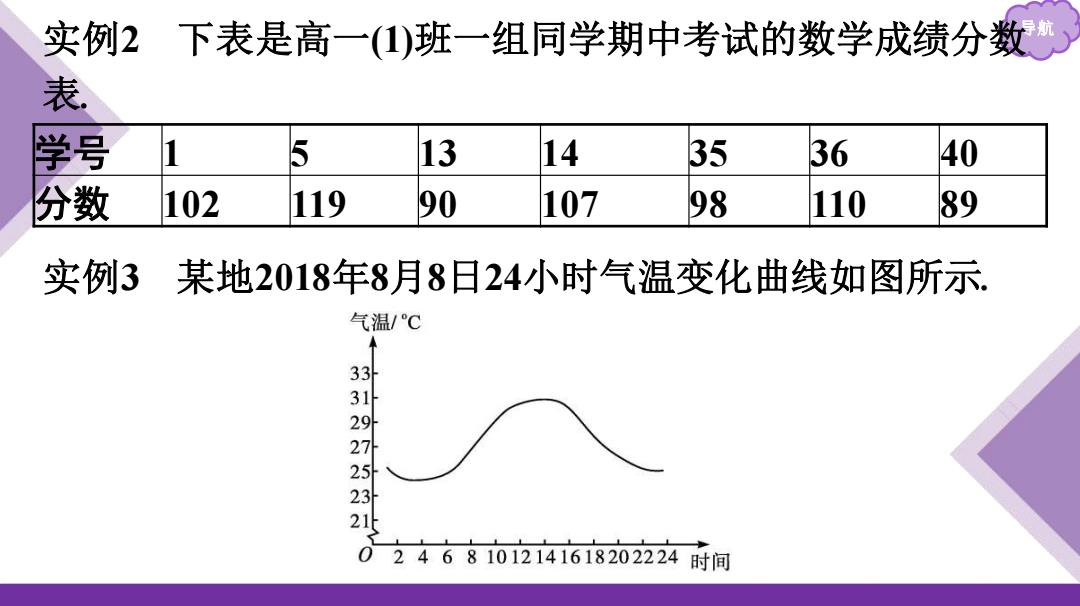
实例 导航 2 下表是高一(1)班一组同学期中考试的数学成绩分数 表. 学号 1 5 13 14 35 36 40 分数 102 119 90 107 98 110 89 实例3 某地2018年8月8日24小时气温变化曲线如图所示

导 ()实例2中的表格能表示两个变量之间存在函数关系吗?如 果能,那么定义域是什么?值域是什么? (2)实例3中的曲线能表示两个变量之间存在函数关系吗?为 什么?如果能,那么自变量是什么? (3)上述三个实例中表示函数的方法分别是什么? (4)实例2和实例3中的函数关系能否用解析式表示?
导航 (1)实例2中的表格能表示两个变量之间存在函数关系吗?如 果能,那么定义域是什么?值域是什么? (2)实例3中的曲线能表示两个变量之间存在函数关系吗?为 什么?如果能,那么自变量是什么? (3)上述三个实例中表示函数的方法分别是什么? (4)实例2和实例3中的函数关系能否用解析式表示?

导 提示:)能.表示数学分数是学号的函数,其中,定义域为 {1,5,13,14,35,36,40},值域为{102,119,90,107,98,110,89}. (2)能.因为对于24时内的任意一个时间,都有唯一确定的气温 的值与之对应,所以存在函数关系,其中自变量是时间. (3)实例1中表示函数的方法是解析法; 实例2中表示函数的方法是列表法; 实例3中表示函数的方法是图象法 (4)不能.并不是所有的函数都有解析式
导航 提示:(1)能.表示数学分数是学号的函数,其中,定义域为 {1,5,13,14,35,36,40},值域为{102,119,90,107,98,110,89}. (2)能.因为对于24时内的任意一个时间,都有唯一确定的气温 的值与之对应,所以存在函数关系,其中自变量是时间. (3)实例1中表示函数的方法是解析法; 实例2中表示函数的方法是列表法; 实例3中表示函数的方法是图象法. (4)不能.并不是所有的函数都有解析式

导航 2.填空: 表示法 定义 解析法 用 表示函数的方法 列表法 用 的形式给出函数的对应关系 图象法 用 表示函数的方法
导航 2 .填空: 表示法 定 义 解析法 用代数式(或解析式)表示函数的方法 列表法 用列表的形式给出函数的对应关系 图象法 用函数的图象表示函数的方法

导航 3.做一做:(1)设在上述所给的实例2中的函数为fx),则 f35)= 答案:98 (2)若函数fx)=x+b,f1)=2,f2)=0,则fx)= 解析:由f1)=22)=0, 得位中。a解得临子 所以fx)=-2x+4. 答案:-2x+4
导航 3.做一做:(1)设在上述所给的实例2中的函数为f(x),则 f(35)= . 答案:98 (2)若函数f(x)=kx+b,f(1)=2,f(2)=0,则f(x)= . 解析:由f(1)=2,f(2)=0, 得 𝒌 + 𝒃 = 𝟐, 𝟐𝒌 + 𝒃 = 𝟎, 解得 𝒌 = -𝟐, 𝒃 = 𝟒, 所以f(x)=-2x+4. 答案:-2x+4

导航 二、函数的图象 【问题思考】 1观察下面的函数图象并回答问题: 函数fx)=x2-2x,x∈【-1,2]的图象如图所示 ()点A,在函数x)的图象上吗? (2)点B(2,)在函数)的图象上吗? (3)函数x)的图象上所有的点的集合应该如何表示?
导航 二、函数的图象 【问题思考】 1.观察下面的函数图象并回答问题: 函数f(x)=x2 -2x,x∈[-1,2]的图象如图所示. (1)点 A 𝟏 𝟐 ,- 𝟏 𝟐 在函数 f(x)的图象上吗? (2)点 B - 𝟏 𝟐 , 𝟓 𝟒 在函数 f(x)的图象上吗? (3)函数f(x)的图象上所有的点的集合应该如何表示?