
全程设计 第四章 指数函数、对数函数与幂函数 4.2.3 对数函数的性质与图象 第2课时 对数函数及其性质的应用
第四章 指数函数、对数函数与幂函数 4.2.3 对数函数的性质与图象 第2课时 对数函数及其性质的应用

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导期 课前·基础认知 对数函数的图象与性质 【问题思考】 1.填空:(1)对于函数fx)=logx(心0,呋1),因为必有1)=0,所以 x)的图象必过点. (2)在函数fx)==log(a>0,呋1)中,_决定fx)的单调性 (3)当m,n∈(0,1)(或m,n∈(1,+oo)时,logmn__0; 当m∈(0,1),n∈(1,+∞)(或m∈(1,+o),n∈(0,1))时,log 20. (4)在第一象限内,自左而右,对数函数的底数依次
导航 课前·基础认知 对数函数的图象与性质 【问题思考】 1.填空:(1)对于函数f(x)=logax(a>0,a≠1),因为必有f(1)=0,所以 f(x)的图象必过(1,0)点. (2)在函数f(x)=logax(a>0,a≠1)中, a 决定f(x)的单调性. (3)当m,n∈(0,1)(或m,n∈(1,+∞))时,logmn > 0; 当m∈(0,1),n∈(1,+∞)(或m∈(1,+∞),n∈(0,1))时,logmn < 0. (4)在第一象限内,自左而右,对数函数的底数依次增大

导航 2.做一做:(1)若函数fx)=log(a2-1x在区间(0,+o)内是减函数, 测实数a的取值范围是 (2)l0g30.3 l0g2.(填“>”“<”或“=”) 答案:(1)(V2,-1)U(1,V2(2)<
导航 2.做一做:(1)若函数f(x)= 在区间(0,+∞)内是减函数, 则实数a的取值范围是 ; (2)log30.3 log52.(填“>”“<”或“=”) 答案:(1)(- 𝟐,-1)∪(1, 𝟐) (2)< lo𝐠(𝒂 𝟐 -𝟏) x

导航 课堂·重难突破 探究一比较大小 【例1】比较下列各组数的大小: (1)l0g2π与l0g20.9;(2)l0g20.3与l0g0.20.3; 3)l0g076与60m.7;(4)1og25与1l0g35. 分析:比较对数值的大小,主要依据对数函数的单调性,同底时 相应的对数函数可直接比较大小;不同底时,可找中间量进行 比较
导航 课堂·重难突破 探究一 比较大小 【例1】比较下列各组数的大小: (1)log2π与log20.9; (2)log20.3与log0.20.3; (3)log0.76与6 0.7 ; (4)log25与log35. 分析:比较对数值的大小,主要依据对数函数的单调性,同底时 相应的对数函数可直接比较大小;不同底时,可找中间量进行 比较

导航 解:(1).函数y=l0g2x在区间(0,+o)内是增函数,π>0.9, 10g2>l0g20.9. (2).10g20.3l0g0.21=0, ∴l0g20.360=1,l0g0.76l0g0.76
导航 解:(1)∵函数y=log2x在区间(0,+∞)内是增函数,π>0.9, ∴log2π>log20.9. (2)∵log20.3log0.21=0, ∴log20.36 0=1,log0.76log0.76
导航 (4)(解法一)函数=l0g2和y=l0g3x的图象如图所示,当x>1 时y=l0g2x的图象在y=l0g3x的图象上方,这里x=5, .l0g25>l0g35. y=log2x (解法)rog5之lg5 y=log3x 又l0gs3>l0gs2>0, 5 .l0gz5>l0g35
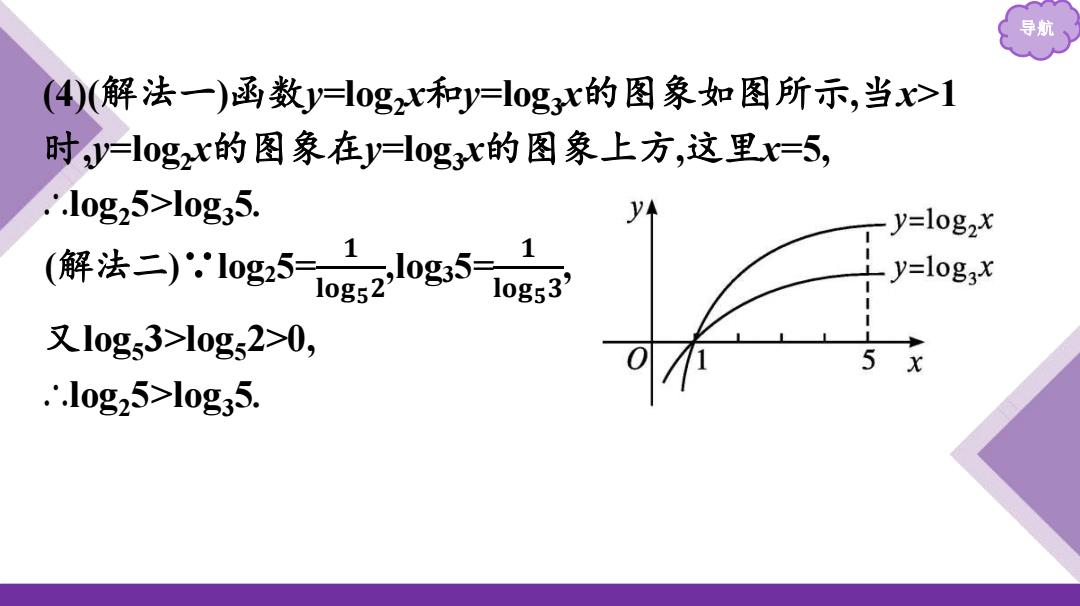
导航 (4)(解法一)函数y=log2x和y=log3x的图象如图所示,当x>1 时,y=log2x的图象在y=log3x的图象上方,这里x=5, ∴log25>log35. (解法二)∵log25= 𝟏 𝐥𝐨𝐠𝟓 𝟐 ,log35= 𝟏 𝐥𝐨𝐠𝟓 𝟑 , 又log53>log52>0, ∴log25>log35

导航 反思感悟比较对数大小的方法 类型 方法 底数相同,真数不同 利用对数函数的单调性 底数不同,真数相同 1.化为同底数;2.利用图象 底数不同,真数不同 利用中间量 指数值与对数值的比较 利用中间量
导航 反思感悟 比较对数大小的方法 类 型 方 法 底数相同,真数不同 利用对数函数的单调性 底数不同,真数相同 1.化为同底数;2.利用图象 底数不同,真数不同 利用中间量 指数值与对数值的比较 利用中间量

导航 【变式训练1】比较下列各组中两个值的大小: (1)ln0.3,ln2; (2)l0g3.1,l0g5.2(a>0,且呋1); (3)l0g30.2,l0g40.2; (4)l0g3π,l0gm3
导航 【变式训练1】比较下列各组中两个值的大小: (1)ln 0.3,ln 2; (2)loga3.1,loga5.2(a>0,且a≠1); (3)log30.2,log40.2; (4)log3π,logπ3

解:1)因为函数y=lnx是增函数,且0.31时,函数y=logx在区间(0,+o)内是增函数,又3.1log5.2. 6)图为0slbe3bgu4所以E0a 3,所以10g3>l0g33=1, 同理,1=l0gm>l0gn3,所以log3>l0gn3
导航 解:(1)因为函数y=ln x是增函数,且0.31时,函数y=logax在区间(0,+∞)内是增函数,又3.1loga5.2. (3)因为 0>log0.23>log0.24,所以 𝟏 𝐥𝐨𝐠𝟎.𝟐 𝟑 3,所以log3π>log33=1. 同理,1=logππ>logπ3,所以log3π>logπ3