
全程设计 2.5.2 圆与圆的位置关系
2.5.2 圆与圆的位置关系
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
导航 素养·目标定位 目标素养 知识概览 1.能根据给定的圆的方 相交:r1-r2kdr1+r2 关系解决相关问题 相离 内含:d<r1-r2l
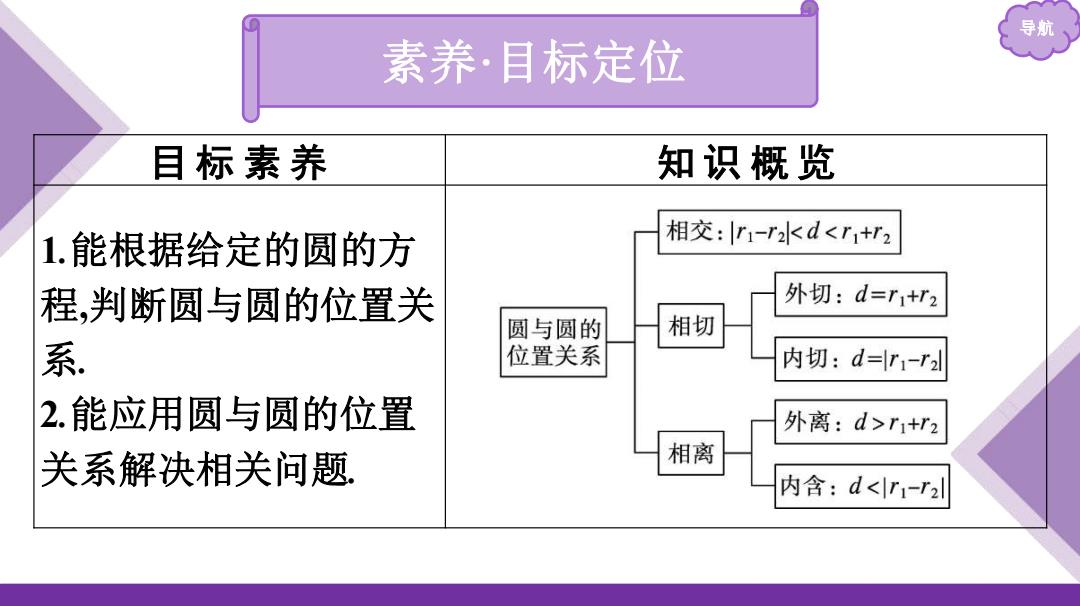
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能根据给定的圆的方 程,判断圆与圆的位置关 系. 2.能应用圆与圆的位置 关系解决相关问题

导航 课前·基础认知 1.用几何法判定圆与圆的位置关系 已知两圆 C1:c-x1)2+0y-y1)2=rr1>0),C2:c-x2)2+0y-y2)2=T22>0), 则圆心距CC=x1-x2)2+0y1y22
导航 课前·基础认知 1.用几何法判定圆与圆的位置关系 已知两圆 C1:(x-x1) 2 +(y-y1) 2 =𝒓𝟏 𝟐 (r1>0),C2:(x-x2) 2 +(y-y2) 2 =𝒓𝟐 𝟐 (r2>0), 则圆心距 d=|C1C2|= (𝒙𝟏-𝒙𝟐) 𝟐 + (𝒚𝟏-𝒚𝟐) 𝟐
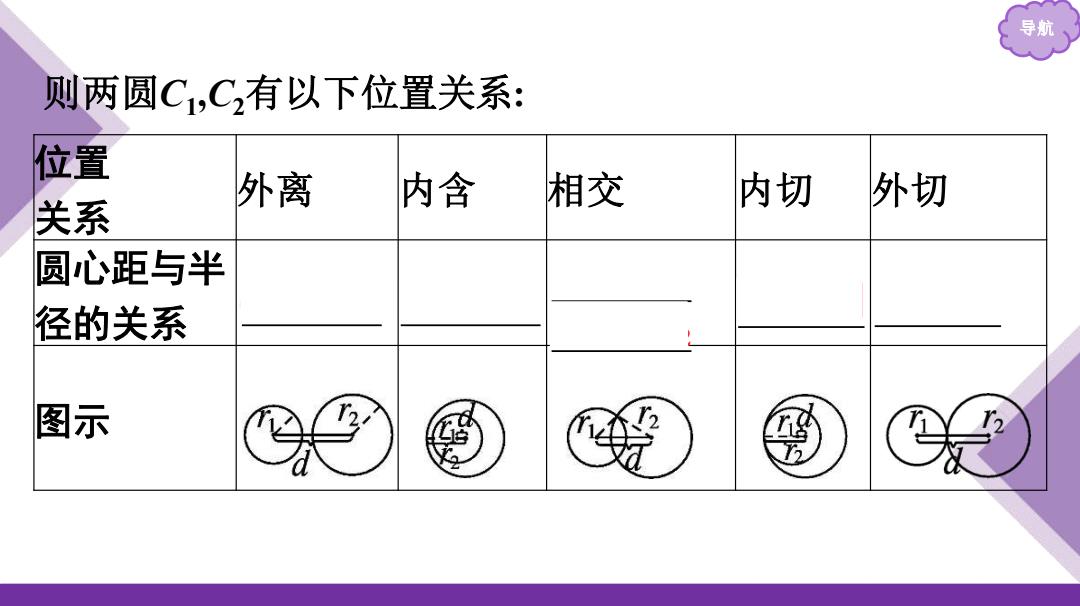
导航 则两圆C,C,有以下位置关系: 位置 外离 内含 相交 内切 外切 关系 圆心距与半 径的关系 图示
导航 则两圆C1 ,C2有以下位置关系: 位置 关系 外离 内含 相交 内切 外切 圆心距与半 径的关系 d>r1+r2 d<|r1 -r2 | |r1 -r2 | <d<r1+r2 d=|r1 -r2 | d=r1+r2 图示

导 微训练圆x+2)2+y2=4与圆(x-2)2+(0y-1)2=9的位置关系为( A.内切 B.相交 C外切 D.外离 答案:B 解析:由题意得两圆的圆心坐标分别为(-2,0),(2,1),则两圆心的 距离d= (-2-2)2+(0-1)2=V7.由于1<k5,故选B
导航 微训练 圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( ) A.内切 B.相交 C.外切 D.外离 答案:B 解析:由题意得两圆的圆心坐标分别为(-2,0),(2,1),则两圆心的 距离d= . (-𝟐-𝟐) 由于1<d<5,故选B. 𝟐 + (𝟎-𝟏) 𝟐 = 𝟏𝟕

导航 2.用代数法判定圆与圆的位置关系 己知两圆C1:x2+y2+D1x+Ey+F1=0(D子+E2-4F>0), C2:x2+y2+D2x+E2y+F2=0(D2+E2-4F2>0),将方程联立 x2+y2+D1x+E1y+F1=0分以下情况: x2+y2+D2x+E2y+F2=0
导航 2.用代数法判定圆与圆的位置关系 已知两圆 C1:x 2 +y2 +D1x+E1y+F1=0(𝑫𝟏 𝟐 + 𝑬𝟏 𝟐 -4F1>0), C2:x 2 +y2 +D2x+E2y+F2=0(𝑫𝟐 𝟐 + 𝑬𝟐 𝟐 -4F2>0),将方程联立 𝒙 𝟐 + 𝒚 𝟐 + 𝑫𝟏 𝒙 + 𝑬𝟏 𝒚 + 𝑭𝟏 = 𝟎, 𝒙 𝟐 + 𝒚 𝟐 + 𝑫𝟐 𝒙 + 𝑬𝟐 𝒚 + 𝑭𝟐 = 𝟎, 分以下情况:
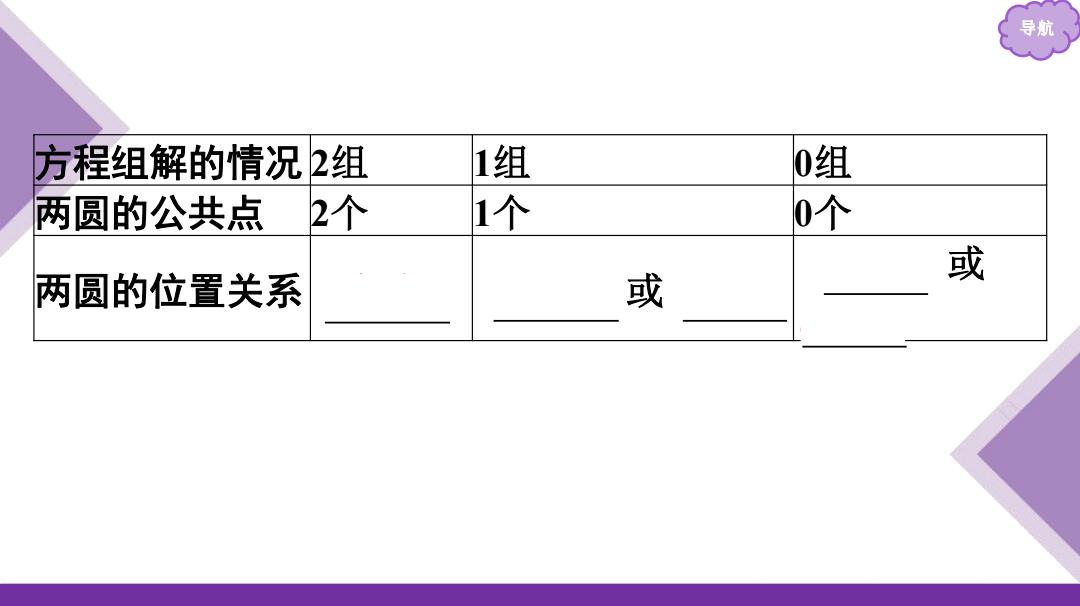
导航 方程组解的情况2组 1组 0组 两圆的公共点2个 1个 0个 或 两圆的位置关系 或
导航 方程组解的情况 2组 1组 0组 两圆的公共点 2个 1个 0个 两圆的位置关系 相交 外切 或 内切 外离 或 内含

导航 微思考将两个相交的非同心圆的方程 x2+y2+Dx+Ey+F=0(=1,2)相减,可得一直线方程,这个直线方 程具有什么样的特殊性呢? 提示:两圆相减得一直线方程,它经过两圆的公共点.经过相交 两圆的公共交点的直线是两圆的公共弦所在的直线
导航 微思考 将两个相交的非同心圆的方程 x 2+y2+Dix+Ei y+Fi =0(i=1,2)相减,可得一直线方程,这个直线方 程具有什么样的特殊性呢? 提示:两圆相减得一直线方程,它经过两圆的公共点.经过相交 两圆的公共交点的直线是两圆的公共弦所在的直线

导航 课堂·重难突破 圆与圆的位置关系的判定 典例剖析 1.已知圆C1x2+y2-2x+4y+2-5=0,圆C2x2+y2+2x-2y+2- 3=0(>0),求当a为何值时,两圆 (1)外切;2)相交;3)外离
导航 课堂·重难突破 一 圆与圆的位置关系的判定 典例剖析 1.已知圆C1 :x 2+y2 -2ax+4y+a2 -5=0,圆C2 :x 2+y2+2x-2ay+a2 - 3=0(a>0),求当a为何值时,两圆 (1)外切;(2)相交;(3)外离