
全程设计 6.2 排列与组合 第4课时 组合的应用
6.2 排列与组合 第4课时 组合的应用
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导期 素养·目标定位 目标素养 1.进一步理解组合的定义,熟练掌握组合数公式的应用. 2.能解决含有限制条件的组合问题,掌握常见的类型及解决策 略. 3.能解决简单的排列、组合的综合问题
导航 目 标 素 养 1.进一步理解组合的定义,熟练掌握组合数公式的应用. 2.能解决含有限制条件的组合问题,掌握常见的类型及解决策 略. 3.能解决简单的排列、组合的综合问题. 素养·目标定位
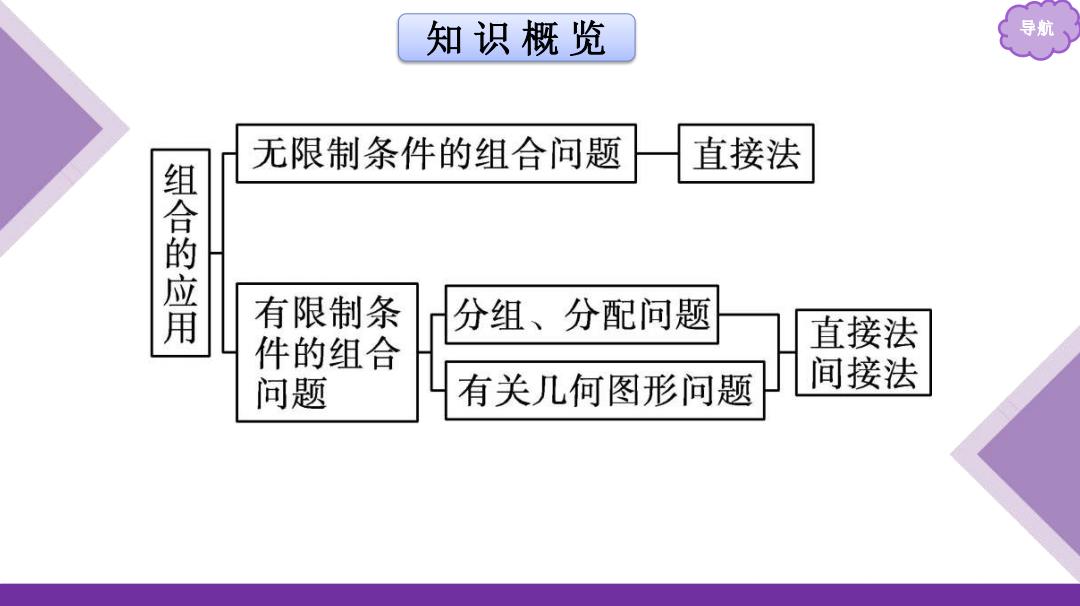
知识概览 导航 无限制条件的组合问题 直接法 组合的应用 有限制条 分组、分配问题 件的组合 直接法 问题 有关几何图形问题 间接法
知 识 概 览 导航

导 课前·基础认知 1组合的有关概念 一般地,从n个不同元素中取出m(m≤m个元素作为一组,叫 做从n个不同元素中取出m个元素的一个组合. 组合数用符号C表示,其公式为 Cm= A = A nm-1-2rnm+m,n∈N,m≤m),特别地,C9= m
导航 1.组合的有关概念 一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫 做从n个不同元素中取出m个元素的一个组合. 组合数用符号𝐂𝒏 𝒎 表示,其公式为 𝐂𝒏 𝒎 = 𝐀𝒏 𝒎 𝐀 𝒎 𝒎 = 𝒏(𝒏-𝟏)(𝒏-𝟐)…(𝒏-𝒎+𝟏) 𝒎! (m,n∈N * ,m≤n),特别地,𝐂𝒏 𝟎 = 𝐂𝒏 𝒏 =1. 课前·基础认知

导航 微思考1应用组合知识解决实际问题的四个步骤是什么? 提示:1)判断:判断实际问题是不是组合问题 (2)方法:选择利用直接法还是间接法解题 (3)计算:利用组合数公式结合两个计数原理计算, (4)结论:根据计算结果写出方案个数
导航 微思考1应用组合知识解决实际问题的四个步骤是什么? 提示:(1)判断:判断实际问题是不是组合问题. (2)方法:选择利用直接法还是间接法解题. (3)计算:利用组合数公式结合两个计数原理计算. (4)结论:根据计算结果写出方案个数

导航 微训练(1)若把4张同样的参观券分给5个人,每人最多分一 张,且全部分完,则分法一共有( A.A种 B.45种 C.54种 D.C种 答案:D 解析:由于4张同样的参观券分给5个人,每人最多分一张,从5 个人中选4人满足分配要求,故有C种
导航 微训练(1)若把4张同样的参观券分给5个人,每人最多分一 张,且全部分完,则分法一共有( ) A.𝐀𝟓 𝟒 种 B.4 5 种 C.5 4 种 D.𝐂𝟓 𝟒 种 答案:D 解析:由于4张同样的参观券分给5个人,每人最多分一张,从5 个人中选4人满足分配要求,故有 𝐂 种. 𝟓 𝟒

(2)某施工小组有男工人7名,女工人3名,现要选1名女工人和 2名男工人去支援另一施工小组,不同的选法有( A.C30种 B.A30种 C.A3A2种 D.CC种 答案:D 解析:每个被选的人都无顺序差别,是组合问题分两步完成:第 一步,选女工人,有C3种选法;第二步,选男工人,有C子种选法.根据 分步乘法计数原理,共有CC子种不同的选法
导航 (2)某施工小组有男工人7名,女工人3名,现要选1名女工人和 2名男工人去支援另一施工小组,不同的选法有( ) A.𝐂𝟏𝟎 𝟑 种 B.𝐀𝟏𝟎 𝟑 种 C.𝐀𝟑 𝟏 𝐀𝟕 𝟐 种 D.𝐂𝟑 𝟏 𝐂𝟕 𝟐 种 答案:D 解析:每个被选的人都无顺序差别,是组合问题.分两步完成:第 一步,选女工人,有𝐂𝟑 𝟏 种选法;第二步,选男工人,有𝐂𝟕 𝟐 种选法.根据 分步乘法计数原理,共有𝐂𝟑 𝟏 𝐂𝟕 𝟐 种不同的选法

导 2组合与排列的异同点 共同点:排列与组合都是从n个不同元素中取出m(m≤n)个 元素 不同点:排列与元素的顺序有关,组合与元素的顺序无关 微思考2解决先选后排问题时,应遵循哪些原则? 提示:1)先特殊后一般;(2)先组合后排列;3)先分类后分步
导航 2.组合与排列的异同点 共同点:排列与组合都是从n个不同元素中取出m(m≤n)个 元素. 不同点:排列与元素的顺序有关,组合与元素的顺序无关. 微思考2解决先选后排问题时,应遵循哪些原则? 提示:(1)先特殊后一般;(2)先组合后排列;(3)先分类后分步

导 课堂·重难突破 有限制条件的组合问题 典例剖析 1.课外活动小组共13人,其中男生8人,女生5人,并且男、女 生各有一名队长,现从中选5人主持某项活动,符合下列条件的 选法各有多少种? (1)至少有一名队长当选; (2)至多有两名女生当选; (3)既要有队长,又要有女生当选; (4)至多有1名队长当选
导航 一 有限制条件的组合问题 典例剖析 1.课外活动小组共13人,其中男生8人,女生5人,并且男、女 生各有一名队长,现从中选5人主持某项活动,符合下列条件的 选法各有多少种? (1)至少有一名队长当选; (2)至多有两名女生当选; (3)既要有队长,又要有女生当选; (4)至多有1名队长当选. 课堂·重难突破