
全程设计 1.1 空间向量及其运算 1.1.1 空间向量及其线性运算
1.1 空间向量及其运算 1.1.1 空间向量及其线性运算
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
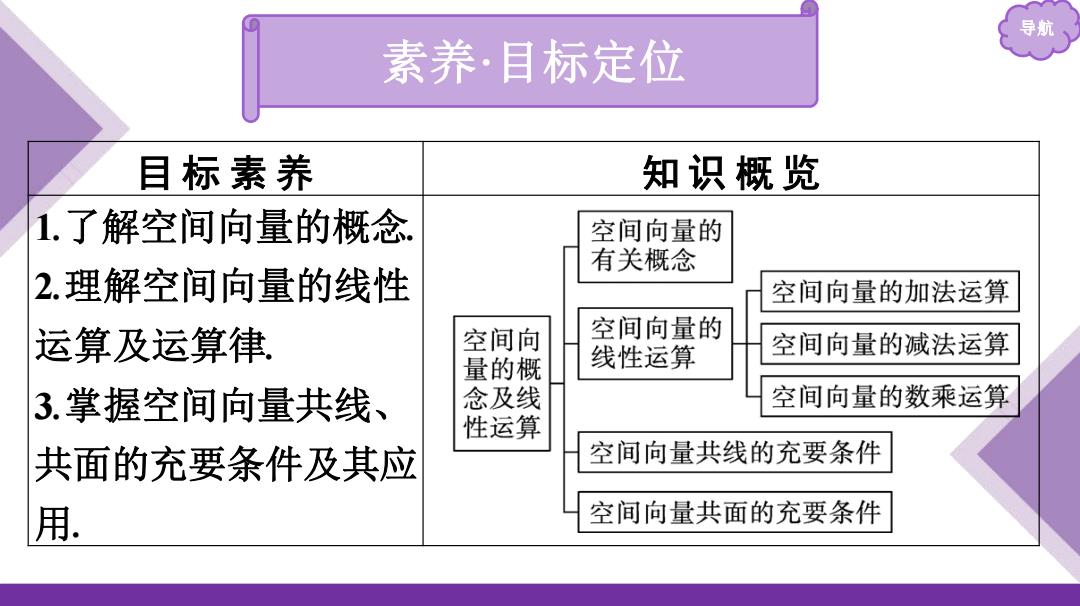
导航 素养·目标定位 目标素养 知识概览 1.了解空间向量的概念 空间向量的 有关概念 2.理解空间向量的线性 空间向量的加法运算 运算及运算律 空间向 空间向量的 线性运算 空间向量的减法运算 量的概 3.掌握空间向量共线、 念及线 空间向量的数乘运算 性运算 共面的充要条件及其应 空间向量共线的充要条件 用. 空间向量共面的充要条件
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.了解空间向量的概念. 2.理解空间向量的线性 运算及运算律. 3.掌握空间向量共线、 共面的充要条件及其应 用

导航 课前·基础认知 1.空间向量的有关概念 1)定义:在空间,我们把具有 和 的量叫做空 间向量. (2)长度或模:空间向量的 叫做空间向量的长度或 模
导航 课前·基础认知 1.空间向量的有关概念 (1)定义:在空间,我们把具有 大小 和 方向 的量叫做空 间向量. (2)长度或模:空间向量的 大小 叫做空间向量的长度或 模
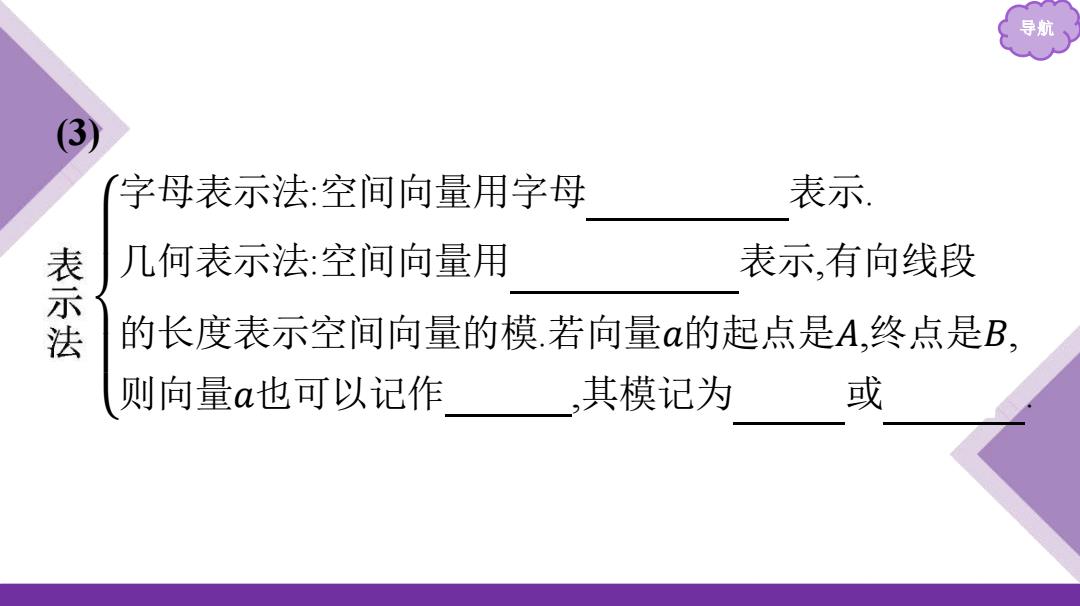
导航 3 字母表示法:空间向量用字母 表示 表示法 几何表示法:空间向量用 表示有向线段 的长度表示空间向量的模若向量α的起点是A,终点是B 则向量a也可以记作,其模记为 或
导航 (3) 字母表示法:空间向量用字母 𝑎,𝑏,𝑐,… 表示. 几何表示法:空间向量用 有向线段 表示,有向线段 的长度表示空间向量的模.若向量 𝑎的起点是 𝐴,终点是 𝐵, 则向量 𝑎也可以记作 𝐴 𝐵 ,其模记为 |𝑎| 或 |𝐴 𝐵 |

导航 微思考空间向量的定义及表示方法与平面向量的定义及表示 方法有区别吗? 提示:空间向量与平面向量的定义没有本质区别,表示方法都 一样
导航 微思考空间向量的定义及表示方法与平面向量的定义及表示 方法有区别吗? 提示:空间向量与平面向量的定义没有本质区别,表示方法都 一样
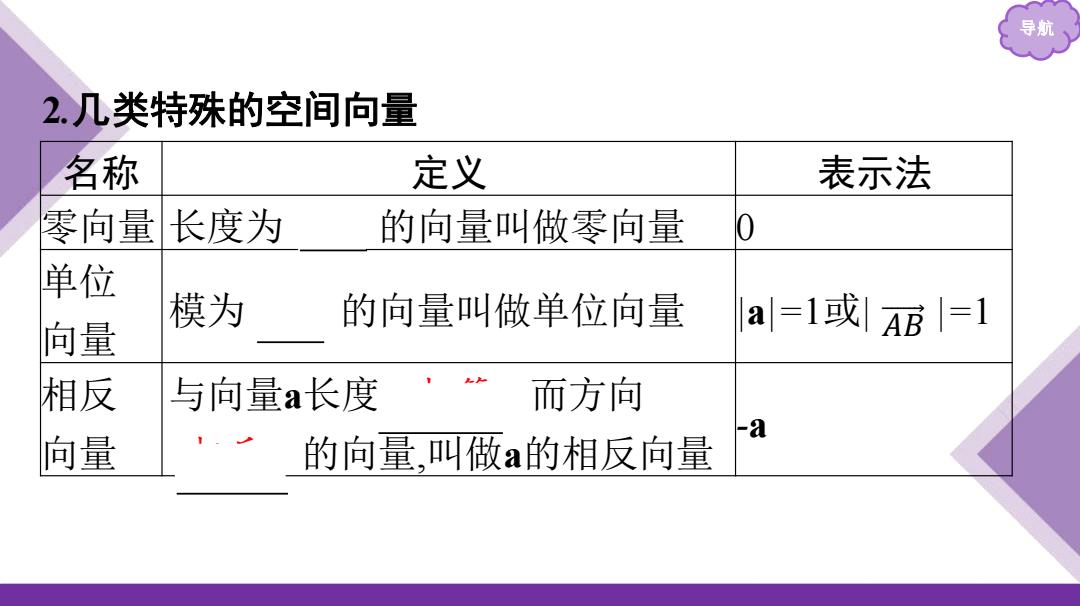
导航 2.几类特殊的空间向量 名称 定义 表示法 零向量长度为 的向量叫做零向量 0 单位 模为 的向量叫做单位向量 向量 a=1或|AB=1 相反 与向量a长度 而方向 -a 向量 的向量,叫做a的相反向量
导航 2.几类特殊的空间向量 名称 定义 表示法 零向量 长度为 0 的向量叫做零向量 0 单位 向量 模为 1 的向量叫做单位向量 |a|=1或| |=1 相反 向量 与向量a长度 相等 而方向 相反 的向量,叫做a的相反向量 -a 𝐴 𝐵

导航 名称 定义 表示法 如果表示若干空间向量的有向线段 共线 所在的直线互相平行或重合,那么这aIb 向量 些向量叫做共线向量或平行向量 规定:零向量与任意向量平行 011 a 相等 方向” 且模 的向量 向量 叫做相等向量 a=b或AB=CD
导航 名称 定义 表示法 共线 向量 如果表示若干空间向量的有向线段 所在的直线互相平行或重合,那么这 些向量叫做共线向量或平行向量 a∥b 规定:零向量与任意向量平行 0∥a 相等 向量 方向 相同 且模 相等 的向量 叫做相等向量 a=b或 𝐴 𝐵 = 𝐶 𝐷
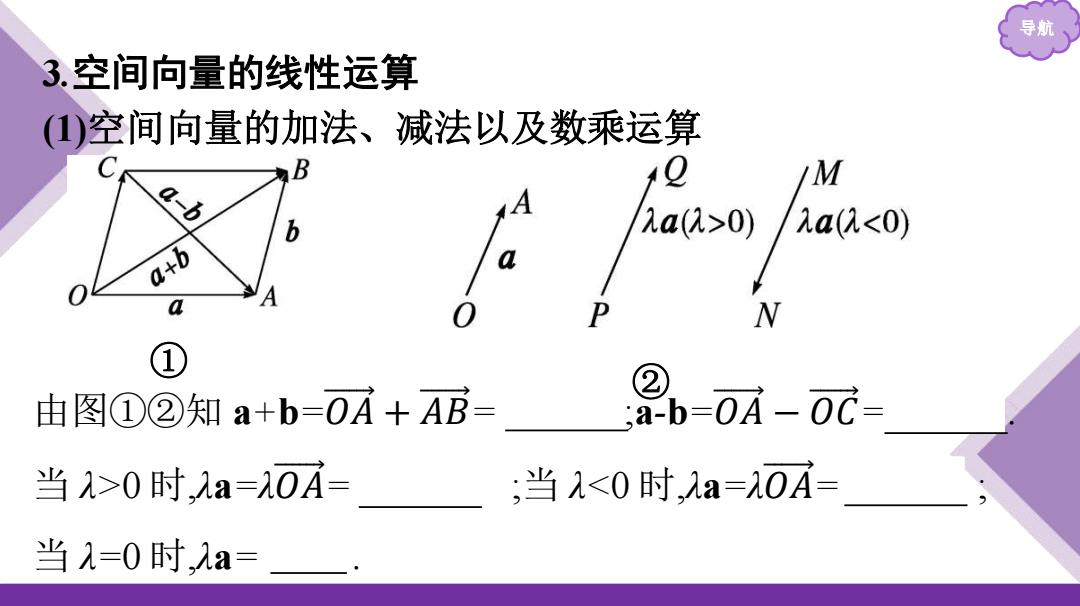
导航 3.空间向量的线性运算 ()空间向量的加法、减法以及数乘运算 M 2a(2>0) 1a(20时,1a=0A= ;当1<0时,λa=0A= 当λ=0时,λa=
导航 3.空间向量的线性运算 (1)空间向量的加法、减法以及数乘运算 ① ② 由图①②知 a+b=𝑂 𝐴 + 𝐴 𝐵 = 𝑂 𝐵 ;a-b=𝑂 𝐴 − 𝑂 𝐶 = 𝐶 𝐴 . 当 λ>0 时,λa=λ𝑂 𝐴 = 𝑃 𝑄 ;当 λ<0 时,λa=λ𝑂 𝐴 = 𝑀 𝑁 ; 当 λ=0 时,λa= 0

导航 (2)空间向量的线性运算满足以下运算律(其中2u∈R) 交换律:a+b=b+a, 结合律:a+(b+c)=(a+b)+c,(ua)=(u)a, 分配律:(+)a=a+ua,λ(a+b)=人a+2b. 微训练化简:5(3a-2b)+4(2b-3a)=
导航 (2)空间向量的线性运算满足以下运算律(其中λ,μ∈R): 交换律:a+b=b+a; 结合律:a+(b+c)=(a+b)+c,λ(μa)=(λμ)a; 分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb. 微训练化简:5(3a-2b)+4(2b-3a)= 3a-2b