
全程设计 8.3.21 圆柱、圆锥、 圆台、球的表面 积和体积
8.3.2 圆柱、圆锥、圆台、球的表面 积和体积

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.圆柱、圆锥、圆台的表面积 底面积:S底= 圆柱 侧面积:S侧=2πrl 表面积:S=
导航 课前·基础认知 1.圆柱、圆锥、圆台的表面积 圆柱 底面积:S 底= πr 2 侧面积:S 侧=2πrl 表面积:S= 2πr(r+l)
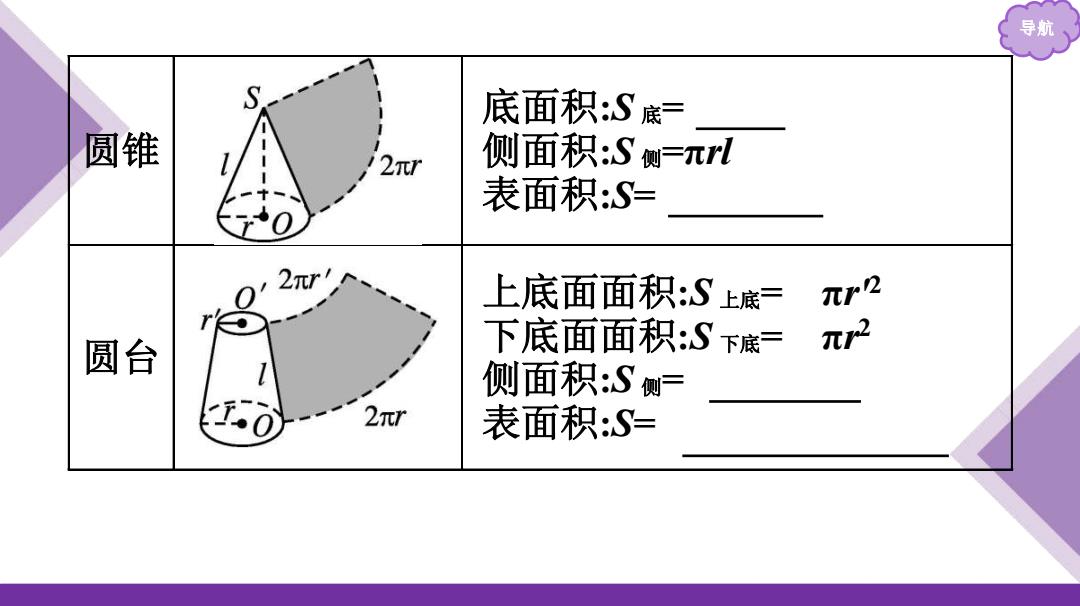
导航 底面积:S底= 圆锥 侧面积:S侧=π 表面积:S= 2πr 上底面面积:S上底= 元r2 圆台 下底面面积:S下底= 元2 侧面积:S侧= 表面积:S=
导航 圆锥 底面积:S 底= πr 2 侧面积:S 侧=πrl 表面积:S= πr(r+l) 圆台 上底面面积:S 上底= πr'2 下底面面积:S 下底= πr 2 侧面积:S 侧= πl(r+r') 表面积:S= π(r'2 +r 2 +r'l+rl)

导航、 2.圆柱、圆锥、圆台的体积公式 圆柱Yh(是底面半径,h是高), V圆锥=3πr2h(r是底面半径,h是高), 圆台n+r+rPr,分别是上、下底面半径h是高
导航 2.圆柱、圆锥、圆台的体积公式 V圆柱=πr 2h(r是底面半径,h是高), V圆锥= πr 2h(r是底面半径,h是高), V圆台= πh(r 2+r'r+r'2 )(r',r分别是上、下底面半径,h是高). 𝟏 𝟑 𝟏 𝟑

导航 微提醒求组合体的表面积和体积,首先要认清组合体是由 哪些简单几何体构成的.组合体的表面积是可见的围成组合 体的所有面的面积之和,但不一定是组成组合体的几个简单 几何体的表面积之和;组合体的体积是构成组合体的几个简 单组合体的体积之和(差)
导航 微提醒 求组合体的表面积和体积,首先要认清组合体是由 哪些简单几何体构成的.组合体的表面积是可见的围成组合 体的所有面的面积之和,但不一定是组成组合体的几个简单 几何体的表面积之和;组合体的体积是构成组合体的几个简 单组合体的体积之和(差)

导航 3.(1)球的表面积 设球的半径为R,则球的表面积S= 微思考球有底面吗?球面能展开成平面图形吗? 提示:球没有底面,球的表面不能展开成平面图形 (2)球的体积 设球的半径为R,则球的体积=
导航 3.(1)球的表面积 设球的半径为R,则球的表面积S= 4πR2 . 微思考 球有底面吗?球面能展开成平面图形吗? 提示:球没有底面,球的表面不能展开成平面图形. (2)球的体积 设球的半径为R,则球的体积V= πR3 . 𝟒 𝟑

导 微探究 (1)若长方体的长、宽、高分别为a,b,c,则其外接 球半径R与三条棱长有何关系? 提示:2R=Va2+b2+c2 (2)棱长为的正方体的外接球,其半径R与棱长有何数量关 系?其内切球呢? 提示:外接球半径R:内切球半径R 3)若一球与正方体的所有棱相切,则球半径R与棱长有何 数量关系? 提示:R=a
导航 微探究 (1)若长方体的长、宽、高分别为a,b,c,则其外接 球半径R与三条棱长有何关系? (2)棱长为a的正方体的外接球,其半径R与棱长a有何数量关 系?其内切球呢? (3)若一球与正方体的所有棱相切,则球半径R与棱长a有何 数量关系? 提示:2R= 𝒂𝟐 + 𝒃𝟐 + 𝒄 𝟐. 提示:外接球半径 R= 𝟑 𝟐 a;内切球半径 R= 𝟏 𝟐 a. 提示:R= 𝟐 𝟐 a

导期 课堂·重难突破 圆柱、圆锥、圆台的表面积 典例剖析 1.(1)一个圆柱的侧面展开图是一个正方形,这个圆柱的表面 积与侧面积的比是(A) A.12B 1+4π C,1+2m D 1+4π 2π 4π 元 2π 解析:设圆柱底面半径为r,则高为2πr,所以圆柱的表面积与 侧面积之比为224+2a:(2aP-12票
导航 课堂·重难突破 一 圆柱、圆锥、圆台的表面积 典例剖析 1.(1)一个圆柱的侧面展开图是一个正方形,这个圆柱的表面 积与侧面积的比是( ) 解析:设圆柱底面半径为r,则高为2πr,所以圆柱的表面积与 侧面积之比为[(2πr) 2+2πr 2 ]∶(2πr) 2= A.𝟏+𝟐𝛑 𝟐𝛑 B.𝟏+𝟒𝛑 𝟒𝛑 C.𝟏+𝟐𝛑 𝛑 D.𝟏+𝟒𝛑 𝟐𝛑 𝟏+𝟐𝛑 𝟐𝛑 . A

(2)已知圆台的上、下底面半径分别是2,6,且侧面面积等于 两底面面积之和. ①求圆台的母线长; ②求圆台的表面积 解:①设圆台的母线长为L,则由题意π(2+6)=πX22+πX62, ∴.8π=40元,∴.=5,∴.该圆台的母线长为5. ②由①可得圆台的表面积为 S=元X(2+6)X5+π22+元X62=40m+4π+36π=80元
导航 (2)已知圆台的上、下底面半径分别是2,6,且侧面面积等于 两底面面积之和. ①求圆台的母线长; ②求圆台的表面积. 解:①设圆台的母线长为l,则由题意π(2+6)l=π×2 2+π×6 2 , ∴8πl=40π,∴l=5,∴该圆台的母线长为5. ②由①可得圆台的表面积为 S=π×(2+6)×5+π·22+π×6 2=40π+4π+36π=80π