
全程设计 第1课时 余弦定理
第1课时 余弦定理

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.余弦定理 文字表述 三角形中任何一边的平方,等于 减去这两边与它们 的两倍
导航 课前 ·基础认知 1 .余弦定理 文字表述 三角形中任何一边的平方,等于 其他两边 平方的和 减去这两边与它们 夹角的余弦 的积 的两倍
导航 符号语言 ax ,b2= c2= cos A= ,cos B= 楼 cos C-
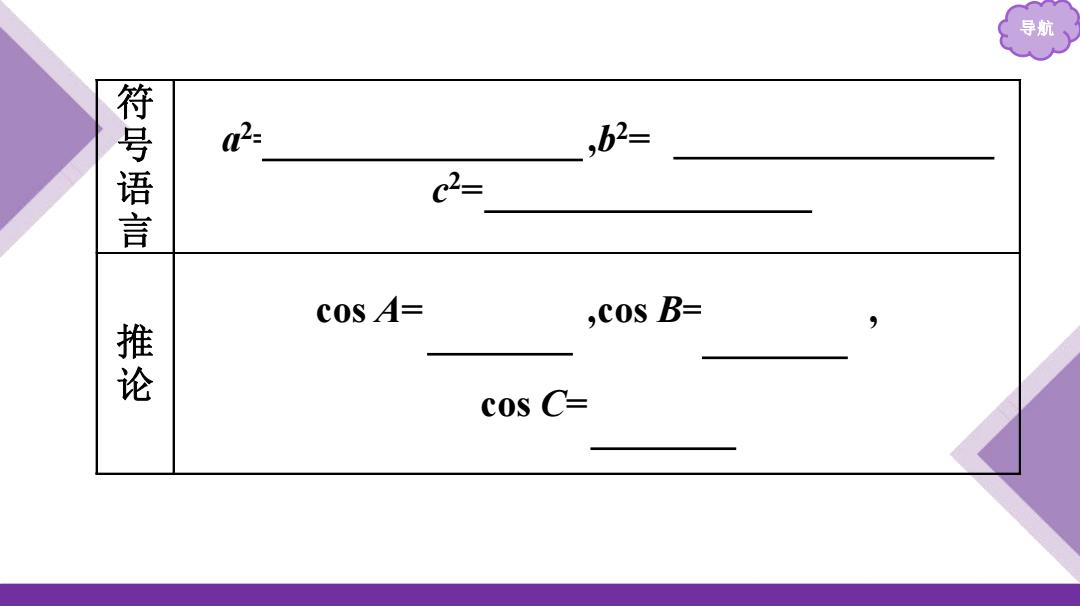
导航 符 号 语 言 a 2 = b 2 +c 2 -2bccos A ,b 2 = a 2 +c 2 -2accos B , c 2 = a 2 +b 2 -2abcos C 推 论 cos A= 𝐛 𝟐 +𝐜 𝟐 -𝐚 𝟐 𝟐𝐛𝐜 ,cos B= 𝐚 𝟐 +𝐜 𝟐 -𝐛 𝟐 𝟐𝐚𝐜 , cos C= 𝐚 𝟐 +𝐛 𝟐 -𝐜 𝟐 𝟐𝐚𝐛

导航 微思考(1)在△ABC中,若2<b2+c2,则△ABC是锐角三角形 吗? 提示:不一定.因为△ABC中a不一定是最大边,所以△ABC 不一定是锐角三角形
导航 微思考 (1)在△ABC中,若a 2<b 2+c 2 ,则△ABC是锐角三角形 吗? 提示:不一定.因为△ABC中a不一定是最大边,所以△ABC 不一定是锐角三角形

导航 (2)在△ABC中,若c2=2+b2,则C=)成立吗?反之,若C=,则 c2=2+b2成立吗?为什么? 提示:成立.因为c2=2+b2,所以2+b2-c2=0,所以 c0sC=2c-0,所以C=五反之,若(-受则cosC-0,即 2ab a2+2-c-0,所以+b-c2=0,即c2=2+b2, 2ab
导航 (2)在△ABC中,若c 2=a 2+b 2 ,则C= 成立吗?反之,若C= ,则 c 2=a 2+b 2成立吗?为什么? 提示:成立.因为c 2=a 2+b 2 ,所以a 2+b 2 -c 2=0,所以 cos C= = 0,所以C= ;反之,若C= ,则cos C=0,即 =0,所以a 2+b 2 -c 2=0,即c 2=a 2+b 2 . 𝛑 𝟐 𝒂 𝟐 + 𝒃 𝟐 -𝒄 𝟐 𝟐𝒂𝒃 𝛑 𝟐 𝒂 𝟐 + 𝒃 𝟐 -𝒄 𝟐 𝟐𝒂𝒃 𝛑 𝟐

导 2.解三角形 )一般地,三角形的 和它们的 叫做三角形的元素. (2)已知三角形的几个元素求 的过程叫做解三 角形. 3.用余弦定理解三角形的问题 利用余弦定理可以解决以下两类问题: (1)已知两边及一角解三角形; (2)已知三边解三角形
导航 2.解三角形 (1)一般地,三角形的 三个角A,B,C 和它们的 对边a,b,c 叫做三角形的元素. (2)已知三角形的几个元素求 其他元素 的过程叫做解三 角形. 3.用余弦定理解三角形的问题 利用余弦定理可以解决以下两类问题: (1)已知两边及一角解三角形; (2)已知三边解三角形

导航 课堂·重难突破 已知两边与一角解三角形 典例剖析 1.(1)在△ABC中,已知=60cm,c=60V3cm,A-E,则 a=cm; (2在△ABC中,若AB=V5,AC=5,且cosC-品,则BC- 答案:(1)60 (2)4或5
导航 课堂·重难突破 一 已知两边与一角解三角形 典例剖析 1.(1)在△ABC中,已知b=60 cm,c=60 cm,A= ,则 a= cm; (2)在△ABC中,若AB= ,AC=5,且cos C= ,则BC= . 答案:(1)60 (2)4或5 𝟑 𝛑 𝟔 𝟓 𝟗 𝟏𝟎

导航 解析:(1)由余弦定理得2=b2+c2-2bc c0sA=602+(60V32-2x60x60V3×c0s03600,故=60cm (2)由余弦定理得AB2=AC2+BC2-2AC·BCC0SC, 即(V5=54BC22x5xBCx品 所以BC29BC+20=0,解得BC=4或BC=5
导航 解析:(1)由余弦定理得 a 2 =b 2 +c 2 -2bc cos A=602 +(60 𝟑) 2 -2×60×60 𝟑×cos 𝛑 𝟔 =3 600,故 a=60 cm. (2)由余弦定理得 AB2 =AC2 +BC2 -2·AC·BC·cos C, 即( 𝟓) 2 =5 2 +BC2 -2×5×BC× 𝟗 𝟏𝟎 , 所以 BC2 -9BC+20=0,解得 BC=4 或 BC=5

导航 规律总结已知三角形的两边及一角解三角形的方法,先利 用余弦定理求出第三边,然后利用余弦定理的推论求出其余 角
导航 规律总结 已知三角形的两边及一角解三角形的方法,先利 用余弦定理求出第三边,然后利用余弦定理的推论求出其余 角