
全程设计 10.1.4 慨率的基本性质
10.1.4 概率的基本性质

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 概率的基本性质 性质1对任意的事件A,都有P(A)≥0. 性质2必然事件的概率为1,不可能事件的概率为0,即 P(2)=,P0)= 性质3如果事件A与事件B互斥,那么P(AUB)=
导航 课前·基础认知 概率的基本性质 性质1 对任意的事件A,都有P(A)≥0. 性质2 必然事件的概率为1,不可能事件的概率为0,即 P(Ω)= 1 ,P( )= 0 . 性质3 如果事件A与事件B互斥,那么P(A∪B)= P(A)+P(B) . ⌀

导航 性质4如果事件A与事件B互为对立事件,那么 P(B)= ,P(A)= 性质5如果ACB,那么P(A) P(B). 性质6设A,B是一个随机试验中的两个事件,我们有 P(AUB)=
导航 性质4 如果事件A与事件B互为对立事件,那么 P(B)= 1-P(A) ,P(A)= 1-P(B) . 性质5 如果A⊆B,那么P(A) ≤ P(B). 性质6 设A,B是一个随机试验中的两个事件,我们有 P(A∪B)= P(A)+P(B)-P(A∩B)

导航 微思考 设事件A发生的概率为P(A),事件B发生的概率为 P(B),那么事件AUB发生的概率是P(A)+P(B)吗? 提示:不一定.当事件A与B互斥时,P(AUB)=P(A)+P(B);当 事件A与B不互斥时,P(AUB)=P(A)+P(B)PA∩B)
导航 微思考 设事件A发生的概率为P(A),事件B发生的概率为 P(B),那么事件A∪B发生的概率是P(A)+P(B)吗? 提示:不一定.当事件A与B互斥时,P(A∪B)=P(A)+P(B);当 事件A与B不互斥时,P(A∪B)=P(A)+P(B)-P(A∩B)
导期 课堂·重难突破 互斥事件、对立事件的概率公式及简单应用 典例剖析 1.备战奥运会射击队的某一选手射击一次,其命中环数的概 率如下表: 命中环数 10环 9环 8环 7环 概率 0.32 0.28 0.18 0.12 若该选手射击一次,求下列事件的概率: (1)命中9环或10环;(2)至少命中8环;3)命中不足8环
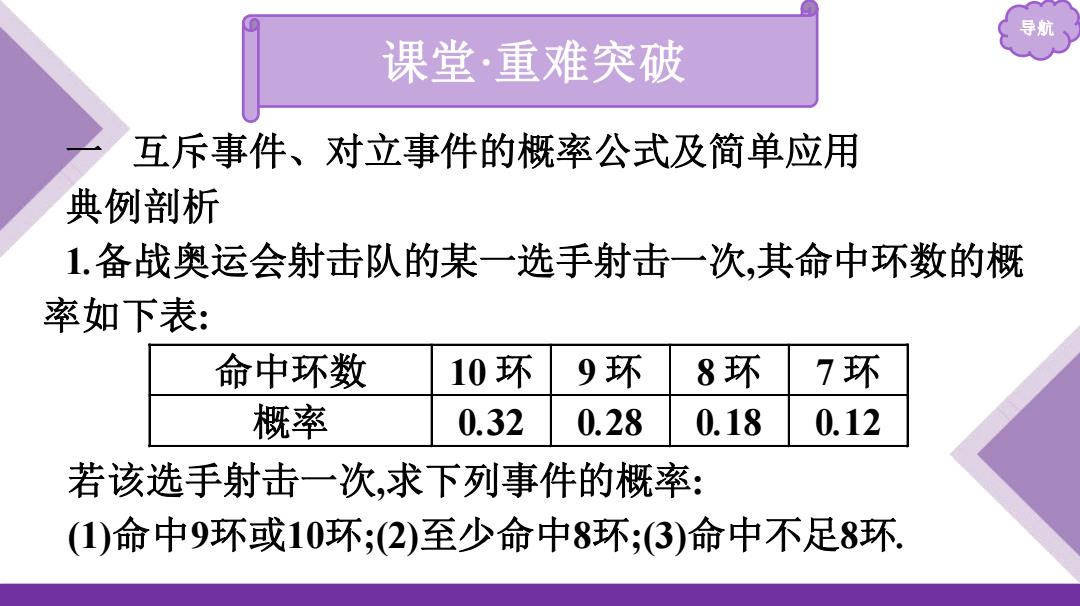
导航 课堂·重难突破 一 互斥事件、对立事件的概率公式及简单应用 典例剖析 1.备战奥运会射击队的某一选手射击一次,其命中环数的概 率如下表: 若该选手射击一次,求下列事件的概率: (1)命中9环或10环;(2)至少命中8环;(3)命中不足8环. 命中环数 10 环 9 环 8 环 7 环 概率 0.32 0.28 0.18 0.12

导航 解:记“射击一次,命中k环”为事件A=7,8,9,10), ()因为A,与A10互斥, 所以P(AgUA10)=P(Ag)+P(A10)=0.28+0.32=0.60. (2)记“至少命中8环”为事件B.B=Ag+Ag十A10,又Ag,Ag,A10两两 互斥,所以P(B)=PAg)+P(Ag)+P(A10)=0.18+0.28+0.32=0.78. 3)记“命中不足8环”为事件C,则事件C与事件B是对立事件 所以P(C)=1-P(B)=1-0.78=0.22
导航 解:记“射击一次,命中k环”为事件Ak (k=7,8,9,10). (1)因为A9与A10互斥, 所以P(A9∪A10)=P(A9 )+P(A10)=0.28+0.32=0.60. (2)记“至少命中8环”为事件B.B=A8+A9+A10,又A8 ,A9 ,A10两两 互斥,所以P(B)=P(A8 )+P(A9 )+P(A10)=0.18+0.28+0.32=0.78. (3)记“命中不足8环”为事件C,则事件C与事件B是对立事件. 所以P(C)=1-P(B)=1-0.78=0.22

规律总结互斥事件、对立事件的概率公式的应用 )互斥事件的概率加法公式P(AUB)=P(A)+P(B)是一个非 常重要的公式,运用该公式解题时,首先要分清事件间是否互 斥,同时要学会把一个事件分拆为几个互斥事件,然后求出各 事件的概率,用加法公式得出结果. (2)当直接计算符合条件的事件的概率比较繁琐时,可间接地 先计算出其对立事件的概率,然后利用对立事件的概率加法 公式P(A)+P(B)=1,求出符合条件的事件的概率
导航 规律总结 互斥事件、对立事件的概率公式的应用 (1)互斥事件的概率加法公式P(A∪B)=P(A)+P(B)是一个非 常重要的公式,运用该公式解题时,首先要分清事件间是否互 斥,同时要学会把一个事件分拆为几个互斥事件,然后求出各 事件的概率,用加法公式得出结果. (2)当直接计算符合条件的事件的概率比较繁琐时,可间接地 先计算出其对立事件的概率,然后利用对立事件的概率加法 公式P(A)+P(B)=1,求出符合条件的事件的概率

导航 二互斥事件、对立事件的概率公式的综合应用典例剖析 2.有A,B,C,D四位贵宾,应分别坐在a,b,c,d四个席位上,现在 这四人均未留意,在四个席位上随便就座时,求: (1)这四人恰好都坐在自己的席位上的概率 (2)这四人恰好都没坐在自己的席位上的概率
导航 二 互斥事件、对立事件的概率公式的综合应用典例剖析 2.有A,B,C,D四位贵宾,应分别坐在a,b,c,d四个席位上,现在 这四人均未留意,在四个席位上随便就座时,求: (1)这四人恰好都坐在自己的席位上的概率; (2)这四人恰好都没坐在自己的席位上的概率

解:将A,B,C,D四位贵宾的就座情况用树状图表示出来: 导航 b 過 b 回回回 司 回 囚 @ 回 回 回 回回④ 回 回回 回 回 回 回四 a 囚 。回回 過 b 回 。回回 d回国 回回 回 回十回 回 回因 回 回 公国
导航 解:将A,B,C,D四位贵宾的就座情况用树状图表示出来: