
全程设计 第五章 三角函数 5.7三角函数的应用
第五章 三角函数 5.7 三角函数的应用

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导期 课前·基础认知 1.函数y=Asin(wx+p),A>0,w>0中参数的物理意义 在物理学中,把物体受到的力(总是指向平衡位置)正比于它离 开平衡位置的距离的运动称为“ ”.在适当的直 角坐标系下,简谐运动可以用函数 表示,其中A>0,ω>0.描述简谐运动的物理量,如振幅、周期和 频率等都与这个解析式中的常数有关
导航 课前·基础认知 1.函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义 在物理学中,把物体受到的力(总是指向平衡位置)正比于它离 开平衡位置的距离的运动称为“ 简谐运动 ” .在适当的直 角坐标系下,简谐运动可以用函数 y=Asin(ωx+φ),x∈[0,+∞) 表示,其中A>0,ω>0.描述简谐运动的物理量,如振幅、周期和 频率等都与这个解析式中的常数有关
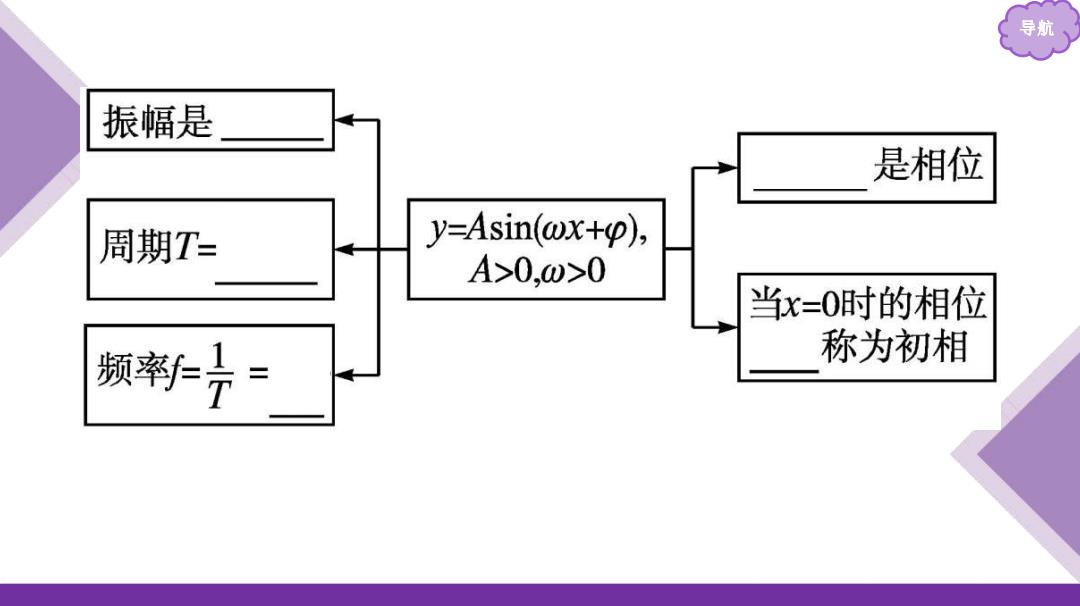
导航 振幅是 是相位 周期T= y=Asin(@x+p), A>0,0>0 当x=0时的相位 颜7 称为初相
导航

微思考1在物理学中,简谐运动的图象就是函数 y=Asin(wx+p)(A>0,w>0),x∈[0,+oo)的图象,其中A>0,w>0.描 述简谐运动的物理量有振幅、周期、频率、相位和初相等 你知道这些物理量分别是指哪些数据以及各自的含义吗? 提示:A是振幅,它是指物体离开平衡位置的最大距离;T2π 是周期,它是指物体往复运动一次所需要的时间,f停-云是 频率,它是指物体在单位时间内往复运动的次数;ωx+0称为相 位;0称为初相,即x=0时的相位
导航 微思考1 在物理学中,简谐运动的图象就是函数 y=Asin(ωx+φ)(A>0,ω>0),x∈[0,+∞)的图象,其中A>0,ω>0.描 述简谐运动的物理量有振幅、周期、频率、相位和初相等, 你知道这些物理量分别是指哪些数据以及各自的含义吗? 提示:A是振幅,它是指物体离开平衡位置的最大距离; 是周期,它是指物体往复运动一次所需要的时间, 是 频率,它是指物体在单位时间内往复运动的次数;ωx+φ称为相 位;φ称为初相,即x=0时的相位. T=𝟐𝛑 𝝎 f=𝟏 𝑻 = 𝝎 𝟐𝛑

导航 微判断(1)物体运动的初始位置即为初相.(√) (2)完成往复运动一次所需要的时间即为一个周期.(√) (3)离开平衡位置的最大距离即为振幅(√)
导航 微判断(1)物体运动的初始位置即为初相.( ) (2)完成往复运动一次所需要的时间即为一个周期.( ) (3)离开平衡位置的最大距离即为振幅.( ) √ √ √

导航 微训练简谐振动,=2sin(x+3)的相位是( A.2 B暗 C.3 D2+3 答案:D
导航 微训练 简谐振动 y=2sin 𝛑 𝟐 𝒙 + 𝟑 的相位是( ) A.2 B. 𝛑 𝟐 C.3 D. 𝛑 𝟐 x+3 答案:D

导期 2.三角函数的应用 )三角函数作为描述现实世界中 的一种数学 模型,可以用来研究很多问题,在刻画周期变化规律、预测其 未来等方面都发挥着十分重要的作用. (2)利用搜集到的数据,先画出相应的“ ”、观察散 点图,然后进行 以获得具体的函数模型,最后利 用这个函数模型来解决相应的实际问题
导航 2.三角函数的应用 (1)三角函数作为描述现实世界中 周期现象 的一种数学 模型,可以用来研究很多问题,在刻画周期变化规律、预测其 未来等方面都发挥着十分重要的作用. (2)利用搜集到的数据,先画出相应的“ 散点图 ”、观察散 点图,然后进行 函数拟合 以获得具体的函数模型,最后利 用这个函数模型来解决相应的实际问题

导航 微思考2散点图在三角函数建模过程中起到什么作用? 提示:利用散点图可较直观地分析两个变量之间的某种关系, 然后利用这种关系选择一种合适的函数去拟合这些,点,从而 避免因盲目选择函数模型造成失误
导航 微思考2 散点图在三角函数建模过程中起到什么作用? 提示:利用散点图可较直观地分析两个变量之间的某种关系, 然后利用这种关系选择一种合适的函数去拟合这些点,从而 避免因盲目选择函数模型造成失误

导期 课堂·重难突破 三角函数模型在物理学中的应用 典例剖析 1.一根细线的一端固定,另一端悬挂一个小球,当小球来回摆动时,离 开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系是 5-6sin(2r+). (1)画出它的图象; (2)回答以下问题: ①小球开始摆动(即仁0),离开平衡位置的位移是多少? ②小球摆动时,离开平衡位置的最大距离是多少? ③小球来回摆动一次需要多少时间?
导航 课堂·重难突破 一 三角函数模型在物理学中的应用 典例剖析 1.一根细线的一端固定,另一端悬挂一个小球,当小球来回摆动时,离 开平衡位置的位移s(单位: cm)与时间t(单位:s)的函数关系是 s=6sin(2πt+ ). (1)画出它的图象; (2)回答以下问题: ①小球开始摆动(即t=0),离开平衡位置的位移是多少? ②小球摆动时,离开平衡位置的最大距离是多少? ③小球来回摆动一次需要多少时间? 𝛑 𝟔