
全程设计 第五章 三角函数 5.3 诱导公式 第2课时 三角函数的诱号公式五六
第五章 三角函数 5.3 诱导公式 第2课时 三角函数的诱导公式五~ 六

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.诱导公式五、六 公式五sinm(.a斤一,cos(分0= 公式六:sin(受+a=_,cos(2+a= 利用公式五或公式六,可以实现 与 的相互转化. 公式一~公式六都叫做
导航 课前·基础认知 1.诱导公式五、六 公式五:sin 𝛑 𝟐 - 𝜶 = cos α ,cos 𝛑 𝟐 -α = sin α . 公式六:sin 𝛑 𝟐 + 𝜶 = cos α ,cos 𝛑 𝟐 +α = -sin α . 利用公式五或公式六,可以实现 正弦函数 与 余弦函数 的相互转化. 公式一~公式六都叫做 诱导公式

导 微点拨记忆规律 ()把角a看作锐角,则2a是第一象限角,-a的正弦函数值 等于角α的余弦函数值u的余弦函数值等于角a的正弦函 数值. (2)把角α看作锐角,则,+a是第二象限角,因此)+的正弦函 数值等于角a的余弦函数值;2+a的余弦函数值等于角a的正 弦函数值的相反数
导航 微点拨记忆规律 (1)把角α看作锐角,则 -α是第一象限角, -α的正弦函数值 等于角α的余弦函数值; -α的余弦函数值等于角α的正弦函 数值. (2)把角α看作锐角,则 +α是第二象限角,因此 +α的正弦函 数值等于角α的余弦函数值; +α的余弦函数值等于角α的正 弦函数值的相反数. 𝛑 𝟐 𝛑 𝟐 𝛑 𝟐 𝛑 𝟐 𝛑 𝟐 𝛑 𝟐

导 微判断(1)诱导公式五、六中的角a只能是锐角.(X) (2)诱导公式五、六与诱导公式一~四的区别在于函数名称要 改变.(√) 3sin(za=±:cosa(k∈Z,(×) 解析:1)诱导公式五、六中的角α是任意角. (2)由诱导公式一~六可知其正确 3)当k=2时,sin(a)=sin(r-a个-sinu
导航 微判断 (1)诱导公式五、六中的角α只能是锐角.( ) (2)诱导公式五、六与诱导公式一~四的区别在于函数名称要 改变.( ) (3)sin =±cos α(k∈Z).( ) 解析:(1)诱导公式五、六中的角α是任意角. (2)由诱导公式一~六可知其正确. (3)当k=2时,sin =sin(π-α)=sin α. 𝒌𝛑 𝟐 -𝜶 𝒌𝛑 𝟐 -𝜶 × √ ×
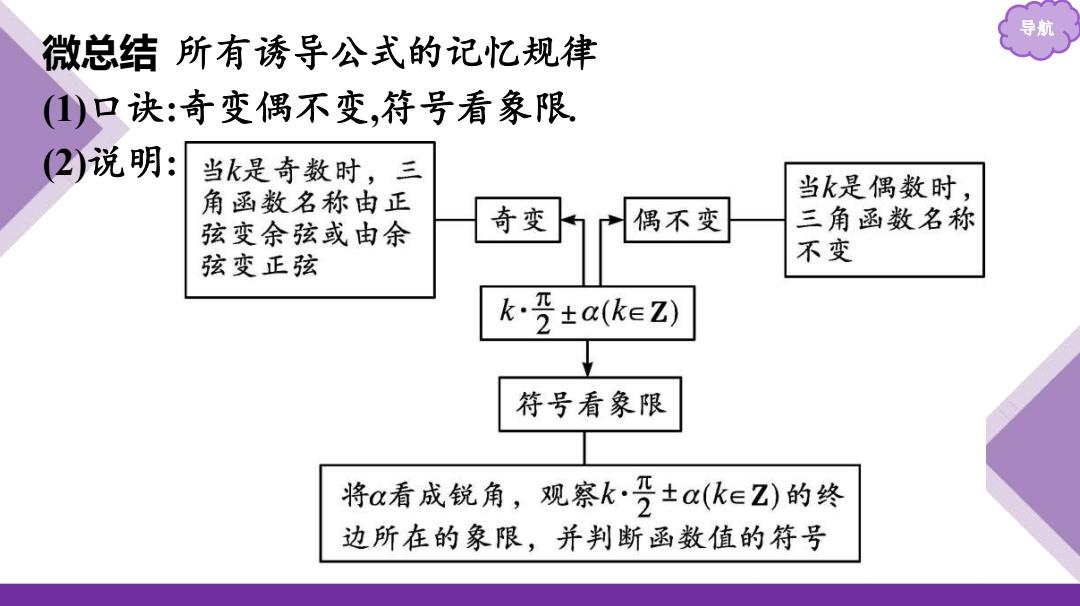
导 微总结所有诱导公式的记忆规律 ()口诀:奇变偶不变,符号看象限 (2)说明: 当k是奇数时,三 角函数名称由正 当k是偶数时, 弦变余弦或由余 奇变 偶不变 三角函数名称 弦变正弦 不变 k·5±a(keZ) 符号看象限 将a看成锐角, 观察k·变±a(keZ)的终 边所在的象限,并判断函数值的符号
导航 微总结 所有诱导公式的记忆规律 (1)口诀 :奇变偶不变 ,符号看象限. (2)说明 :
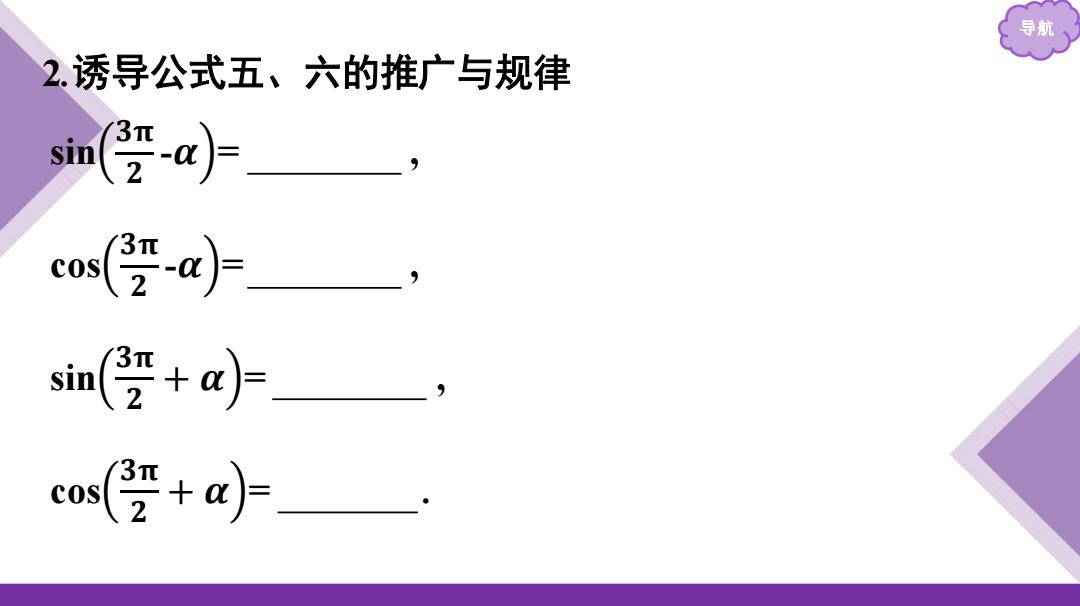
导航 2.诱导公式五、六的推广与规律 sin(a)= 二 os(受+a)
导航 2 .诱导公式五、六的推广与规律 sin 𝟑 𝛑𝟐 -𝜶 = -cos α , cos 𝟑 𝛑𝟐 -𝜶 = -sin α , sin 𝟑 𝛑𝟐 + 𝜶 = -cos α , cos 𝟑 𝛑𝟐 + 𝜶 = sin α
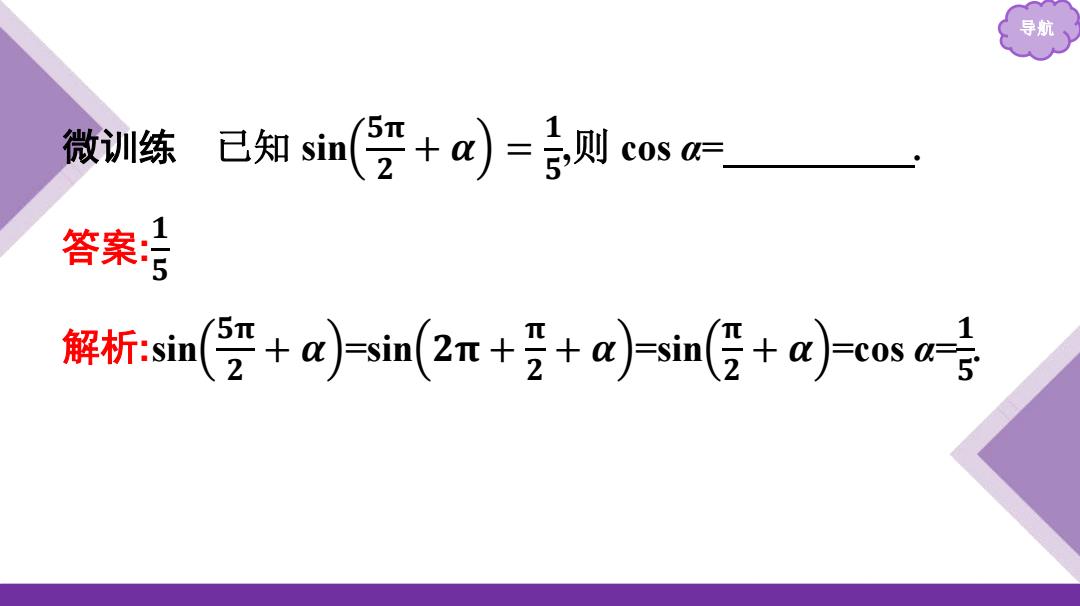
导航 微训练已知sin(罗+m)=则cose 答案号 解析:sin(俨+a-sin(2m+罗+asin(侵+a)-cosa-号
导航 微训练 已知 sin 𝟓𝛑 𝟐 + 𝜶 = 𝟏 𝟓 ,则 cos α= . 答案: 𝟏 𝟓 解析:sin 𝟓𝛑 𝟐 + 𝜶 =sin 𝟐𝛑 + 𝛑 𝟐 + 𝜶 =sin 𝛑 𝟐 + 𝜶 =cos α= 𝟏 𝟓

导航 课堂·重难突破 利用诱导公式化简求值 典例剖 1.化简: in(4π-acos(2z+a tan(5π-a) sin1@cos(Zn-c) sin(3r-ag)sin(受a 解:原式-sina-sina -tang sin2a 1 1-sin2a (-c0s)c0S0 sinacosa cos2a c0s2-1. cos-a
导航 课堂·重难突破 一 利用诱导公式化简求值 典例剖析 1.化简: 𝐬𝐢𝐧(𝟒𝛑-𝜶)𝐜𝐨𝐬 𝟗𝛑 𝟐 +𝜶 𝐬𝐢𝐧 𝟏𝟏𝛑 𝟐 +𝜶 𝐜𝐨𝐬(𝟐𝛑-𝜶) − 𝐭𝐚𝐧(𝟓𝛑-𝜶) 𝐬𝐢𝐧(𝟑𝛑-𝜶)𝐬𝐢𝐧 𝛑 𝟐 -𝜶 . 解:原式= (-𝐬𝐢𝐧𝜶)(-𝐬𝐢𝐧𝜶) (-𝐜𝐨𝐬𝜶)𝐜𝐨𝐬𝜶 − -𝐭𝐚𝐧𝜶 𝐬𝐢𝐧𝜶𝐜𝐨𝐬𝜶 =- 𝐬𝐢𝐧 𝟐 𝜶 𝐜𝐨𝐬 𝟐 𝜶 + 𝟏 𝐜𝐨𝐬 𝟐 𝜶 = 𝟏-𝐬𝐢𝐧 𝟐 𝜶 𝐜𝐨𝐬 𝟐 𝜶 = 𝐜𝐨𝐬 𝟐 𝜶 𝐜𝐨𝐬 𝟐 𝜶 =1

导航 二利用诱导公式证明三角恒等式 典例剖析 2,求证:an2-sin:2-cos6m-_-tanu sin(a+3cos(a+
导航 二 利用诱导公式证明三角恒等式 典例剖析 2.求证: 𝐭𝐚𝐧(𝟐𝛑-𝜶)𝐬𝐢𝐧(-𝟐𝛑-𝜶)𝐜𝐨𝐬(𝟔𝛑-𝜶) 𝐬𝐢𝐧 𝜶+ 𝟑𝛑 𝟐 𝐜𝐨𝐬 𝜶+ 𝟑𝛑 𝟐 =-tan α