
全程设计 第三章 数的概念与性质 3.1 丞数的概念及其表示 3.1.2 函数的表示法
第三章 函数的概念与性质 3.1 函数的概念及其表示 3.1.2 函数的表示法

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
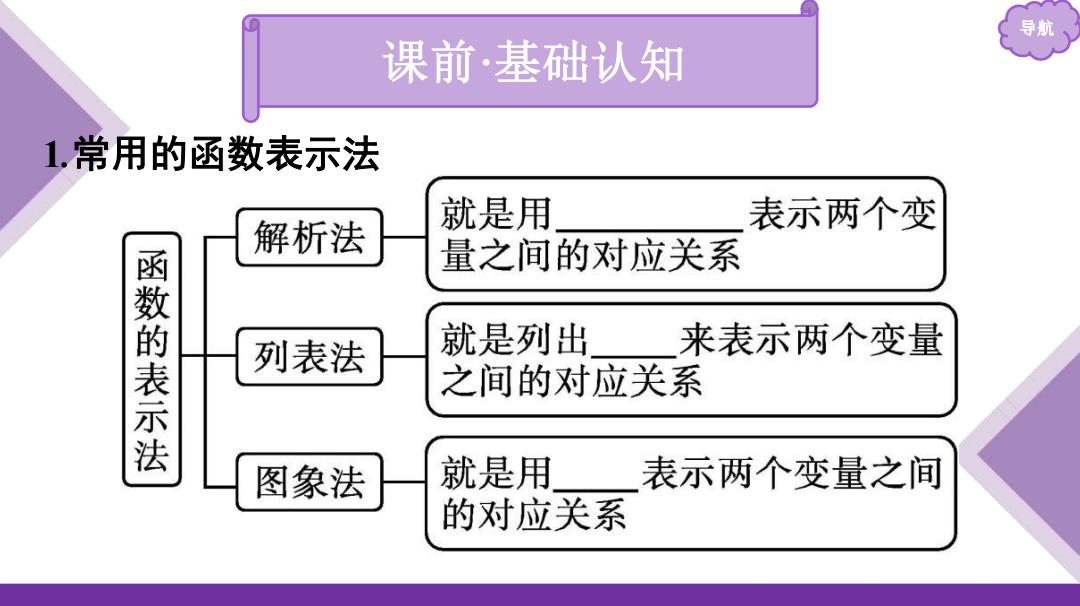
导航 课前·基础认知 1,常用的函数表示法 就是用 表示两个变 解析法 量之间的对应关系 函数的表示法 列表法 就是列出 来表示两个变量 之间的对应关系 图象法 就是用 表示两个变量之间 的对应关系
导航 课前 ·基础认知 1 .常用的函数表示 法

导 微思考1任何一个函数都可以用解析法、列表法、图象法三 种形式表示吗? 提示:不一定 并不是所有的函数都可以用解析式表示,不仅如此,图象法也 不适用于所有函数,如DW-0,x为有理数 列表法虽在理论 (1,x为无理数. 上适用于所有函数,但对于自变量有无数个取值的情况,列表 法只能表示函数的一个概况或片段
导航 微思考1 任何一个函数都可以用解析法、列表法、图象法三 种形式表示吗? 提示:不一定. 并不是所有的函数都可以用解析式表示,不仅如此,图象法也 不适用于所有函数,如 列表法虽在理论 上适用于所有函数,但对于自变量有无数个取值的情况,列表 法只能表示函数的一个概况或片段. D(x)= 𝟎,𝒙为有理数, 𝟏,𝒙为无理数
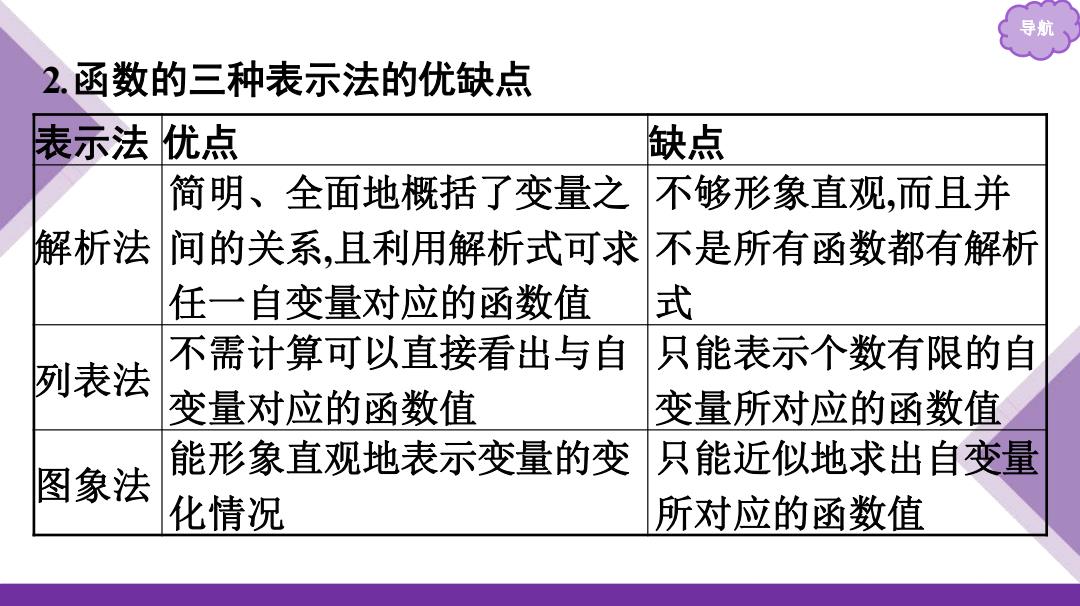
导期 2.函数的三种表示法的优缺点 表示法优点 缺点 简明、全面地概括了变量之 不够形象直观,而且并 解析法 间的关系,且利用解析式可求不是所有函数都有解析 任一自变量对应的函数值 式 不需计算可以直接看出与自 只能表示个数有限的自 列表法 变量对应的函数值 变量所对应的函数值 能形象直观地表示变量的变 只能近似地求出自变量 图象法 化情况 所对应的函数值
导航 2.函数的三种表示法的优缺点 表示法 优点 缺点 解析法 简明、全面地概括了变量之 间的关系,且利用解析式可求 任一自变量对应的函数值 不够形象直观,而且并 不是所有函数都有解析 式 列表法 不需计算可以直接看出与自 变量对应的函数值 只能表示个数有限的自 变量所对应的函数值 图象法 能形象直观地表示变量的变 化情况 只能近似地求出自变量 所对应的函数值

导航 3.分段函数 如果函数y=fx),x∈A,根据自变量x在A中不同的取值范围,有 着不同的对应关系,则称这样的函数为分段函数 微思考2分段函数是一个函数还是几个函数? 提示:分段函数是一个函数,而不是几个函数
导航 3.分段函数 如果函数y=f(x),x∈A,根据自变量x在A中不同的取值范围,有 着不同的对应关系,则称这样的函数为分段函数. 微思考2 分段函数是一个函数还是几个函数? 提示:分段函数是一个函数,而不是几个函数

导航 课堂·重难突破 函数的三种表示方法 典例剖析 1.某商场新进了10台彩电,每台售价3000元,试求售出台数 x(单位:台)与销售收入y(单位:元)之间的函数关系,分别用列 表法、图象法、解析法表示出来
导航 课堂·重难突破 一 函数的三种表示方法 典例剖析 1.某商场新进了10台彩电,每台售价3 000元,试求售出台数 x(单位:台)与销售收入y(单位:元)之间的函数关系,分别用列 表法、图象法、解析法表示出来

导航 解:①列表表示如下: X 1 2 3 4 5 y 3000 6000 9000 12000 15000 x 6 7 8 9 10 y 18000 21000 24000 27000 30000
导航 解:①列表表示如下: x 1 2 3 4 5 y 3 000 6 000 9 000 12 000 15 000 x 6 7 8 9 10 y 18 000 21 000 24 000 27 000 30 000

导航 ②图象法:如图所示 y/元 30000 27000 24000 21000 18000 15000 12000 9000 6000 ● 3000 0 12345678910x/台 ③解析法y=3000xx∈{1,2,3,…,10}
导航 ②图象法:如图所示. ③解析法:y=3 000x,x∈{1,2,3,…,10}

导航 规律总结 列表法、图象法和解析法是从三个不同的角度刻画自变量与 函数值的对应关系,同一个函数可以用不同的方法表示在用 三种方法表示函数时要注意:()解析法必须注明函数的定义 域;2)列表法中选取的自变量要有代表性,应能反映定义域的 特征;3)图象法中要注意是否连线
导航 列表法、图象法和解析法是从三个不同的角度刻画自变量与 函数值的对应关系,同一个函数可以用不同的方法表示.在用 三种方法表示函数时要注意:(1)解析法必须注明函数的定义 域;(2)列表法中选取的自变量要有代表性,应能反映定义域的 特征;(3)图象法中要注意是否连线