
全程设计 第三章 函数的慨念与性质 3.3 幂丞数
第三章 函数的概念与性质 3.3 幂函数

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.幂函数的概念 般地,函数 叫做幂函数,其中 是自变量, 是常数 微思考怎样判断一个函数是不是幂函数? 提示:判断一个函数是不是幂函数,就是看函数表达式是不是 y=x(a为常数)的形式,即函数的解析式为一个幂的形式,且需 满足:(1)指数为常数;(2)底数为自变量;3)系数为1
导航 课前·基础认知 1.幂函数的概念 一般地,函数 y=xα 叫做幂函数,其中 x 是自变量, α 是常数. 微思考 怎样判断一个函数是不是幂函数? 提示:判断一个函数是不是幂函数,就是看函数表达式是不是 y=xα (α为常数)的形式,即函数的解析式为一个幂的形式,且需 满足:(1)指数为常数;(2)底数为自变量;(3)系数为1

导航 2.幂函数的图象与性质 y个 4 y=x3 ()幂函数的图象 3 y=x2 y=x2 Y=x 在同一平面直角坐标系中, 2 y=xi 幂函数y=x,yx2y=x3,y=x2y=x1-3-2 -1 y=x-1 01 234X 的图象如图所示 y=x-1 -1 -2 y=x3 3
导航 2 .幂函数的图象与性质 (1)幂函数的图象 在同一平面直角坐标系中 , 幂函数y=x ,y=x2 ,y=x3 ,y= ,y=x - 1 的图象如图所示 . 𝒙 𝟏𝟐
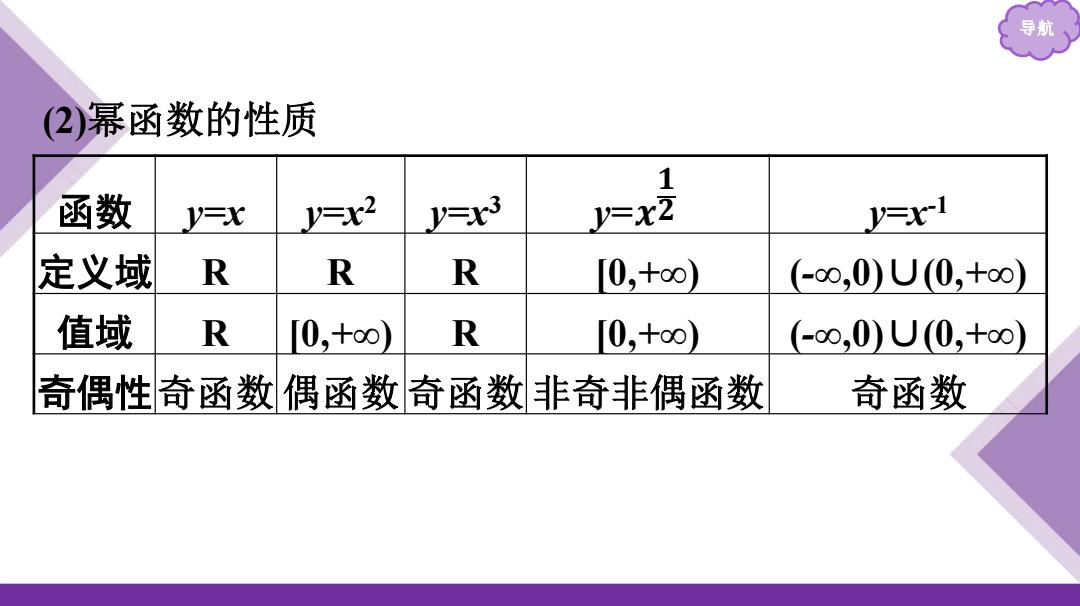
导航 (2)幂函数的性质 函数 y=x y=x2 y=x3 y=x2 y=x1 定义域 R R R 0,+o0) (-0,0)U(0,+oo) 值域 R [0,+o∞) R 0,+o0) (-o0,0)U(0,+o0) 奇偶性奇函数偶函数奇函数非奇非偶函数 奇函数
导航 (2)幂函数的性质 函数 y=x y=x2 y=x3 y= y=x-1 定义域 R R R [0,+∞) (-∞,0)∪(0,+∞) 值域 R [0,+∞) R [0,+∞) (-∞,0)∪(0,+∞) 奇偶性奇函数 偶函数 奇函数 非奇非偶函数 奇函数 𝒙 𝟏 𝟐

导航 1 函数 V-X y=x2 =3 V=x y=x1 在区间 在R上 (-∞,0]上单 在R上 在区间 在区间(-o0,0) 单调性单调递 调递减,在 内单调递减, i 单调递 [0,+o∞)内 增 区间0,+o)增 单调递增 在区间(0,+∞) 内单调递增 内单调递减
导航 函数 y=x y=x2 y=x3 y= y=x-1 单调性 在R上 单调递 增 在区间 (-∞,0]上单 调递减,在 区间[0,+∞) 内单调递增 在R上 单调递 增 在区间 [0,+∞)内 单调递增 在区间(-∞,0) 内单调递减, 在区间(0,+∞) 内单调递减 𝒙 𝟏 𝟐

导月 3)幂函数性质的延伸 ①当a>0时,幂函数的图象过 两点;当a0时,幂函数的图象在区间0,+∞)内单调递 ;特别 地,当a>1时,幂函数的图象在区间(0,+oo)内下凸;当0<<1时, 幂函数的图象在区间0,+∞)内上凸. 当<0时,幂函数的图象在区间(0,+o∞)内单调递
导航 (3)幂函数性质的延伸 ①当α>0时,幂函数的图象过 (0,0) , (1,1) 两点;当α0时,幂函数的图象在区间(0,+∞)内单调递 增 ;特别 地,当α>1时,幂函数的图象在区间(0,+∞)内下凸;当0<α<1时, 幂函数的图象在区间(0,+∞)内上凸. 当α<0时,幂函数的图象在区间(0,+∞)内单调递 减

导航 课堂·重难突破 幂函数的图象及应用 典例剖析 1.已知幂函数fx)=x的图象过点P(2,),试画出fx)的图象并 指出该函数的定义域与单调区间
导航 课堂·重难突破 一 幂函数的图象及应用 典例剖析 1.已知幂函数f(x)=xα的图象过点P(2, ),试画出f(x)的图象并 指出该函数的定义域与单调区间. 𝟏 𝟒

导 解函数)的图象过点P2,, 2)2解得a=2, '.fx)=x2 x)的图象如图所示. fx)的定义域为(-∞,0)U(0,+∞),单调递减区间为(0,+oo),单调递 增区间为(-oo,0)
导航 解:∵函数 f(x)的图象过点 P(2,𝟏 𝟒 ), ∴f(2)= 𝟏 𝟒 ,∴2 α = 𝟏 𝟒 ,解得 α=-2, ∴f(x)=x-2 . f(x)的图象如图所示. f(x)的定义域为(-∞,0)∪(0,+∞),单调递减区间为(0,+∞),单调递 增区间为(-∞,0)

规律总结 1.幂函数的图象一定出现在第一象限内,一定不会出现在第四 象限内,图象最多只能同时出现在两个象限内,至于是否在第 二或第三象限内出现要看幂函数的奇偶性.y 2.幂函数y=x的图象分布与幂指数a的关 系具有如下规律:在直线x=1的右侧,按“逆 时针”方向,图象所对应的幂指数依次增大 (1,1) (如图), 3.根据图象研究函数解析式时,应结合函数O x=1 在第一象限的单调性确定y=a中a的符号
导航 1.幂函数的图象一定出现在第一象限内,一定不会出现在第四 象限内,图象最多只能同时出现在两个象限内,至于是否在第 二或第三象限内出现要看幂函数的奇偶性. 2.幂函数y=xα的图象分布与幂指数α的关 系具有如下规律:在直线x=1的右侧,按“逆 时针”方向,图象所对应的幂指数依次增大 (如图). 3.根据图象研究函数解析式时,应结合函数 在第一象限的单调性确定y=xα中α的符号