
》课圳外国语学校 深圳市新课程新教材高中数学在线教学 《集合与常用逻辑用语》 章末复习课 主讲人:深圳外国语学校朱红光
章末复习课 主讲人:深圳外国语学校 朱红光 《集合与常用逻辑用语》
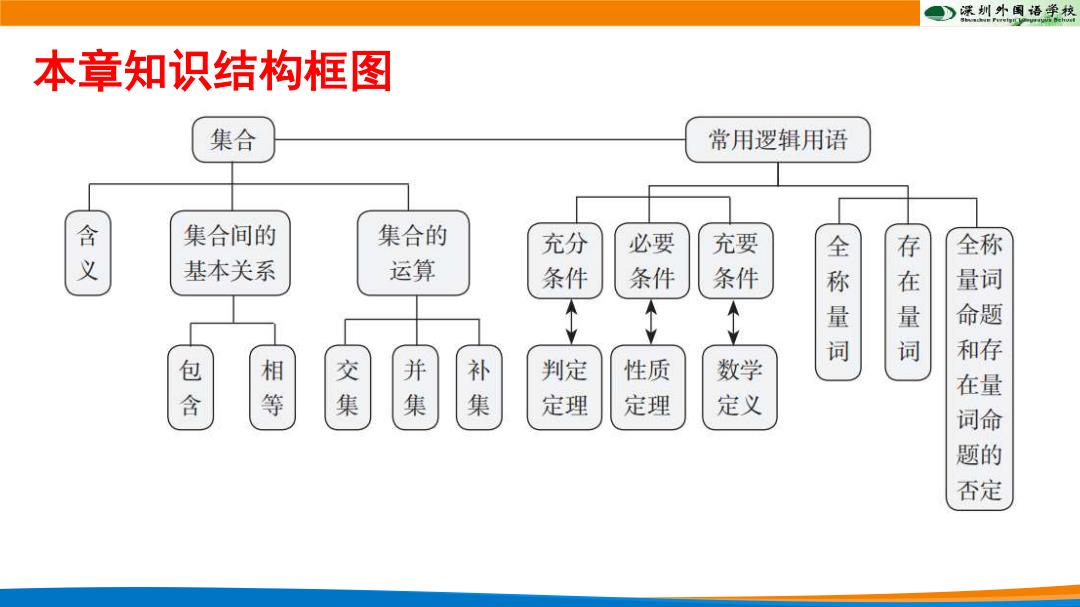
课圳外国语单校 本章知识结构框图 集合 常用逻辑用语 含义 集合间的 集合的 充分 必要 充要 存 全称 基本关系 运算 条件 条件 条件 称量 在 量词 量 命题 和存 包 相 交 并 补 判定 性质 数学 在量 含 等 集 定理 定理 定义 词命 题的 否定
本章知识结构框图

》课圳外国语单校 为什么学习集合? x2-2=0,x∈Z ◆明确研究对象、确定研究范围是研究数学问题的基础; ◆把研究对象放在一起作为一个整体看待,就形成一个集合; ◆集合是刻画一类事物的语言和工具; ◆使用集合的语言和工具,可以简洁、准确地表述研究对象及研究范围; ◆集合语言是数学的基本语言,是现代数学的基础:
为什么学习集合? ◆明确研究对象、确定研究范围是研究数学问题的基础; ◆把研究对象放在一起作为一个整体看待,就形成一个集合; ◆使用集合的语言和工具,可以简洁、准确地表述研究对象及研究范围; ◆集合语言是数学的基本语言,是现代数学的基础. ◆集合是刻画一类事物的语言和工具; x − 2 = 0,x Z 2

●》课圳外国语校 为什么学习逻辑用语? ◆数学知识是建立在有限的定义和公理基础上的一系列数学推理; ◆数学的重要特征是它的严谨性; ◆使用常用逻辑用语表达数学对象、进行数学推理, 可以提高交流的严谨性 和准确性,提升逻辑推理素养; ◆逻辑用语是数学语言的重要组成部分,是数学表达和交流的工具,是逻辑 思维的基本语言
为什么学习逻辑用语? ◆使用常用逻辑用语表达数学对象、进行数学推理,可以提高交流的严谨性 和准确性,提升逻辑推理素养; ◆逻辑用语是数学语言的重要组成部分,是数学表达和交流的工具,是逻辑 思维的基本语言. ◆数学的重要特征是它的严谨性; ◆数学知识是建立在有限的定义和公理基础上的一系列数学推理;

深圳外国语单校 集合与常用逻辑用语都是刻画事物的语言和工具,因此是学 习所有数学内容的基础 具体的初中 集合和常用逻辑用语 抽象的高中 数学知识 数学知识
集合和常用逻辑用语 集合与常用逻辑用语都是刻画事物的语言和工具,因此是学 习所有数学内容的基础. 具体的初中 数学知识 抽象的高中 数学知识

》深圳外国语争校 典型例题 类型一、集合的概念与集合中的元素 例1.己知集合A={1,2,3,4,5},集合B={(x,y)川x∈A,y∈A,x-y∈},则B中所含元 素的个数为() A.3 B.6 C.8 D.10 解:由x-y∈A可知,必有x>y; 当x=2时,y=1; 当x=3时,y=1或y=2: 当x=4时,y=1或y=2或y=3; 当x=5时,y=1或y=2或y=3或y=4;
典型例题 类型一、集合的概念与集合中的元素 解:

》深圳外国语单校 典型例题 类型一、集合的概念与集合中的元素 例2.已知集合A={yly=x2,x∈R,B=yly=x+2,x∈R,则A∩B=( A.{(-1,1),(2,4)} B.{(-1,1)} C.{1,4} D.yly≥0} A={y|y≥0},B=R 解:由 y=x2 解得x=-1,y=1或x=2,y=4, y=x+2
典型例题 类型一、集合的概念与集合中的元素 解: A ={y | y 0},B = R

》深圳外国语学校 典型例题 类型二、集合间的基本关系 例3.已知集合A={L,3,a2},B=1,a+2},是否存在实数a,使得AUB=A?若存在, 试求出实数a的值;若不存在,请说明理由. 确定性 解:由AUB=A可得BsA,所以有1∈A且a+2eA, 无序性 所以a+2=3或a+2=a2,即a=1或a=-1或a=2 互异性 当a=1或-1时,集合A中=1,不符合题意,舍去: 当a=2时,A={1,3,4},B={1,4,B三A满足题意 综上,a=2
典型例题 类型二、集合间的基本关系 解: 确定性 无序性 互异性

》课圳外国语学校 典型例题 类型二、集合间的基本关系 BCA 变式:已知集合A={x|-x2+3x+10>0},B={xm+1<x<2m-1},若A∩B=B, 求实数m的取值范围. 空集是任意集合的子集 解:当B=Φ即m+1≥2m-1时, 当B≠Φ即m+1<2m-1时
典型例题 类型二、集合间的基本关系 变式:已知集合 { | 3 10 0} { | 1 2 1} 2 A = x −x + x + ,B = x m+ x m− ,若 AB = B , 求实数m 的取值范围. 空集是任意集合的子集 解: 当B = 即m +1 2m −1时, 当B 即m +1 2m −1时, B A

》深圳外围语净校 典型例题 类型三、集合的运算 X 例4.已知集合A={x0s2},B={xlas≤a十3} (1)若(CR4)UB=R,求a的取值范围; 2 (2)是否存在a使(CRA)UB=R且A∩B=O? 解:'A={x0s2},.CR4=x0或心2} (2)满足A∩B=Φ需 (1) .'(C RA)UB=R a>2或a+32或a<-3 a≤0, a+3≥2, ∴.-1≤a≤0 显然无解,故不存在这样的☑
典型例题 类型三、集合的运算 解: (1) (2)满足 需 a 2或a +3 0 显然无解,故不存在这样的 a 0 2 x 0 2 x A B = 即a 2或a −3