
全程设计 数学建模 建立丞数模型解快实际问题
数学建模 建立函数模型解决实际问题

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
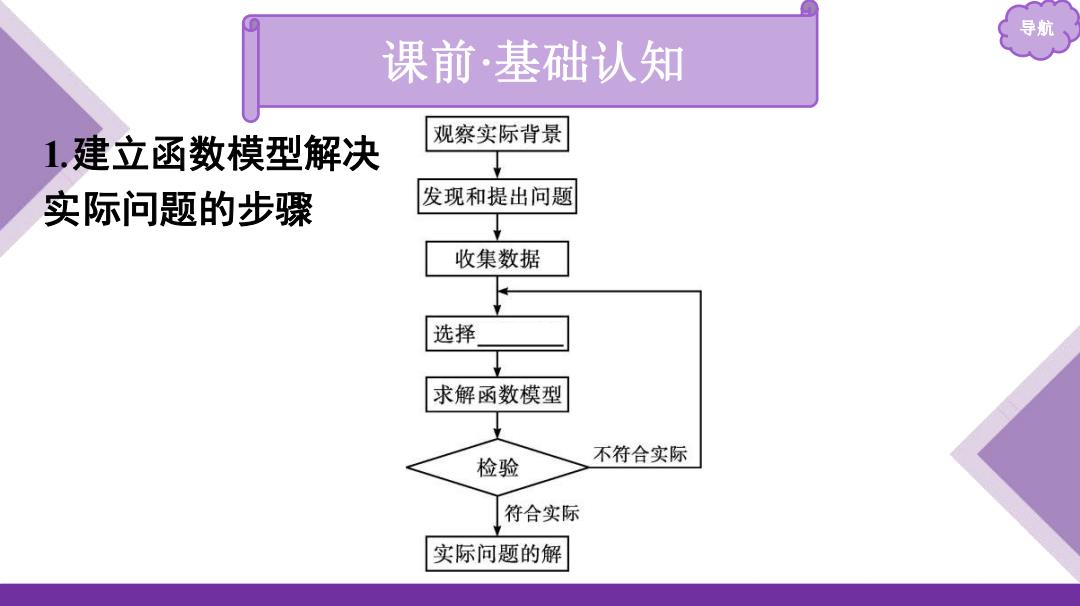
导航 课前·基础认知 1建立函数模型解决 观察实际背景 实际问题的步骤 发现和提出问题 收集数据 选择 求解函数模型 检验 不符合实际 符合实际 实际问题的解
导航 课前 ·基础认知 1 .建立函数模型解决 实际问题的步骤

微判断(1)在构建函数模型时,经常会遇到没有现成数据可用 的情况,这时就需要先收集数据(V (2)在用函数构建数学模型解决实际问题时,首先要对实际问 题中的变化过程进行分析,分析出其中的常量、变量及其相 互关系.(√) (3)求出函数模型后,还需要利用函数模型的解说明实际问题 的变化规律,从而达到解决问题的目的.(√)
导航 微判断(1)在构建函数模型时,经常会遇到没有现成数据可用 的情况,这时就需要先收集数据.( ) (2)在用函数构建数学模型解决实际问题时,首先要对实际问 题中的变化过程进行分析,分析出其中的常量、变量及其相 互关系.( ) (3)求出函数模型后,还需要利用函数模型的解说明实际问题 的变化规律,从而达到解决问题的目的.( ) √ √ √

导航 2.数学建模活动的要求 (1)组建合作团队;2)开展研究活动:3)撰写研究报告; (4)交流展示. 微思考根据散点图选择函数模型时主要依据函数的什么 性质? 提示:主要依据函数的单调性及函数增长速度的快慢
导航 2.数学建模活动的要求 (1)组建合作团队;(2)开展研究活动;(3)撰写研究报告; (4)交流展示. 微思考 根据散点图选择函数模型时主要依据函数的什么 性质? 提示:主要依据函数的单调性及函数增长速度的快慢

导航 课堂·重难突破 数学建模主要步骤的探究 典例剖析 某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种 植成本Q(单位:元10kg)与上市时间(单位:10天)的数据如 下表: 时间t 5 11 25 30 40 种植成本O 15 10.8 15 21 41.5
导航 课堂·重难突破 数学建模主要步骤的探究 典例剖析 某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种 植成本Q(单位:元/10 kg)与上市时间t(单位:10天)的数据如 下表: 时间t 5 11 25 30 40 种植成本Q 15 10.8 15 21 41.5

导航 1)根据上表数据建立一个合适的函数模型描述该蔬菜种植 成本Q与上市时间的变化关系 (2)利用所求的函数模型,求该蔬菜种植成本最低时的上市天 数及最低种植成本
导航 (1)根据上表数据建立一个合适的函数模型描述该蔬菜种植 成本Q与上市时间t的变化关系. (2)利用所求的函数模型,求该蔬菜种植成本最低时的上市天 数及最低种植成本

导航 解:() 0 ①画散点图. 以上市时间(单位:10天) 为横坐标,以种植成本 45405050 Q(单位:元/10kg)为纵坐 标,画出散点图(如图) 1510 0510152025303540 t
导航 解 :(1) ①画散点图 . 以上市时间 t (单位:10 天 ) 为横坐标 ,以种植成本 Q (单位 : 元/10 kg)为纵坐 标 ,画出散点图 (如图 )

②求函数模型 从散点图可以看出,随着的变化,O的值先减小后增大,所以可 以建立二次函数模型 用函数模型Q=+bt什c(a,b,c为常数,0)描述该蔬菜种植成 本Q与上市时间的变化关系. 将表格所提供的前三组数据分别代入Q=t+bt什C, a 15=25a+5b+c, 20 得{10.8=121a+11b+c,解得b= 3 15=625a+25b+c, 所以035 c= 20 2什4
导航 ②求函数模型. 从散点图可以看出,随着t的变化,Q的值先减小后增大,所以可 以建立二次函数模型. 用函数模型Q=at2+bt+c(a,b,c为常数,a≠0)描述该蔬菜种植成 本Q与上市时间t的变化关系. 将表格所提供的前三组数据分别代入Q=at2+bt+c, 得 𝟏𝟓 = 𝟐𝟓𝒂 + 𝟓𝒃 + 𝒄, 𝟏𝟎.𝟖 = 𝟏𝟐𝟏𝒂 + 𝟏𝟏𝒃 + 𝒄, 𝟏𝟓 = 𝟔𝟐𝟓𝒂 + 𝟐𝟓𝒃 + 𝒄, 解得 𝒂 = 𝟏 𝟐𝟎 , 𝒃 = - 𝟑 𝟐 , 𝒄 = 𝟖𝟓 𝟒 . 所以 Q= 𝟏 𝟐𝟎 t 2 - 𝟑 𝟐 t+𝟖𝟓 𝟒
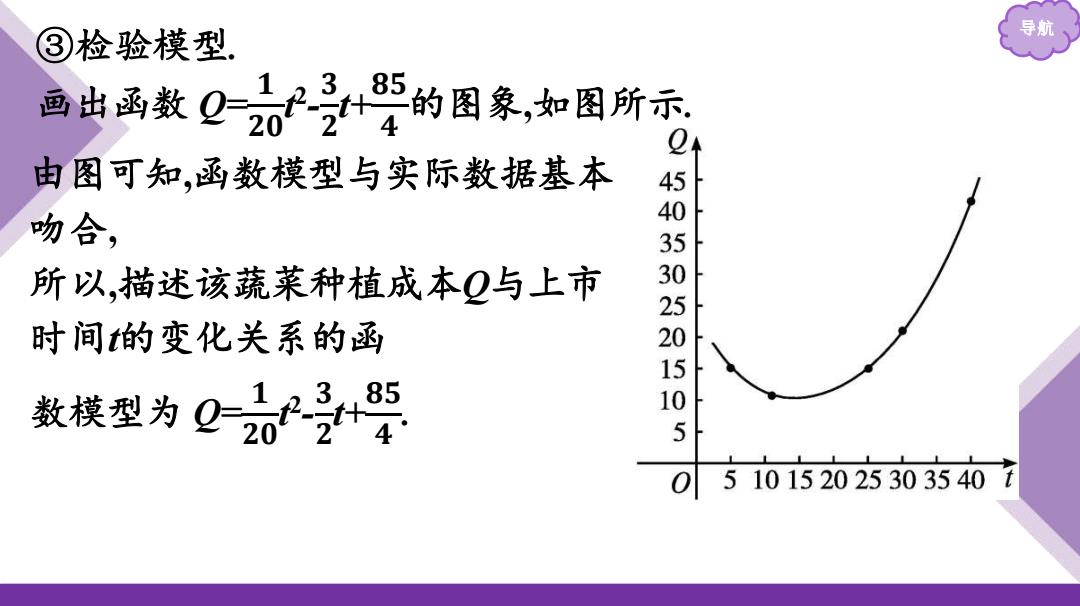
③检验模型, 导航 画出函数Q2臣的困象,知困所示 123 由图可知,函数模型与实际数据基本 吻合, 所以,描述该蔬菜种植成本Q与上市 时间的变化关系的函 505050150 数模型为Q28阳 0510152025303540 t
导航 ③检验模型. 画出函数 Q= 𝟏 𝟐𝟎 t 2 - 𝟑 𝟐 t+𝟖𝟓 𝟒 的图象,如图所示. 由图可知,函数模型与实际数据基本 吻合, 所以,描述该蔬菜种植成本Q与上市 时间t的变化关系的函 数模型为 Q= 𝟏 𝟐𝟎 t 2 - 𝟑 𝟐 t+𝟖𝟓 𝟒