
全程设计 第一章 集合与常用逻辑用语 1.1 集合的概念 第1课时 集合的相关概念
第一章 集合与常用逻辑用语 1.1 集合的概念 第1课时 集合的相关概念

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导期 课前·基础认知 1,元素与集合的相关概念 )元素:一般地把 统称为元素,常用小写拉丁字 母 表示 (2)集合:一些 组成的总体叫做集合(简称为集),常用 大写拉丁字母 表示 3)集合相等:只要构成两个集合的元素是 的,就称这 两个集合是相等的. (4)集合中元素的特征: 和
导航 课前·基础认知 1.元素与集合的相关概念 (1)元素:一般地,把 研究对象 统称为元素,常用小写拉丁字 母 a,b,c, … 表示. (2)集合:一些 元素 组成的总体叫做集合(简称为集),常用 大写拉丁字母 A,B,C, … 表示. (3)集合相等:只要构成两个集合的元素是 一样 的,就称这 两个集合是相等的. (4)集合中元素的特征: 确定性、互异性和 无序性

导航 微思考某班身高高于175厘米的男生能否组成一个集合? 提示:某班身高高于175厘米的男生能组成一个集合,因为标 准确定 微训练英语单词mathematics(数学)中所有英文字母构成的 集合有 个元素 答案:8
导航 微思考 某班身高高于175厘米的男生能否组成一个集合? 提示:某班身高高于175厘米的男生能组成一个集合,因为标 准确定. 微训练 英语单词mathematics(数学)中所有英文字母构成的 集合有 个元素. 答案:8

导航 2.元素与集合的关系 关系 概念 记法 读法 如果a 集合A的元 属于 “a属于A” 素,就说a属于集合A 如果a一·集合A的 不属于 “a不属于A” 元素,就说a不属于集合A
导航 2.元素与集合的关系 关系 概念 记法 读法 属于 如果a 是 集合A的元 素,就说a属于集合A a∈A “a属于A” 不属于 如果a 不是 集合A的 元素,就说a不属于集合A a∉A “a不属于A

导航 微解读(1)符号“∈”“度”刻画的是元素与集合之间的关系.对 于一个元素a与一个集合A而言,只有“M∈A”与“度A”这两种 结果 (2)“∈”和“度”具有方向性,左边是元素,右边是集合,形如R∈0 是错误的
导航 微解读 (1)符号“∈”“∉”刻画的是元素与集合之间的关系.对 于一个元素a与一个集合A而言,只有“a∈A”与“a∉A”这两种 结果. (2)“∈”和“∉”具有方向性,左边是元素,右边是集合,形如R∈0 是错误的
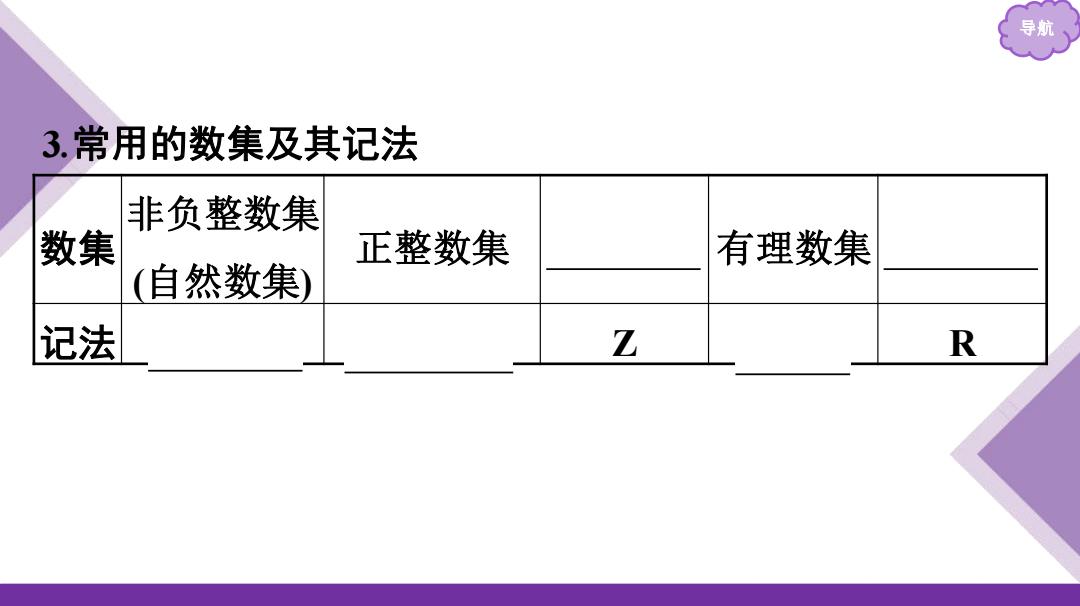
导航 3.常用的数集及其记法 非负整数集 数集 正整数集 有理数集 (自然数集) 记法 Z R
导航 3.常用的数集及其记法 数集 非负整数集 (自然数集) 正整数集 整数集 有理数集 实数集 记法 N N*或N+ Z Q R

导航 课堂·重难突破 集合的基本概念 典例剖析 1判断下列说法是否正确,并说明理由: (1)某个公司里所有的年轻人组成一个集合; (2由1,,引,组成的集合中有5个元素: 3)当a,b,c互不相等时,由a,b,c组成的集合与由b,4,c组成的集 合是相等的
导航 课堂·重难突破 一 集合的基本概念 典例剖析 1.判断下列说法是否正确,并说明理由: (1)某个公司里所有的年轻人组成一个集合; (3)当a,b,c互不相等时,由a,b,c组成的集合与由b,a,c组成的集 合是相等的. (2)由 1,𝟑 𝟐 , 𝟔 𝟒 , - 𝟏 𝟐 , 𝟏 𝟐 组成的集合中有 5 个元素;

解:(1)不正确.因为“年轻人”没有确定的标准,对象不具有确定 性,所以不能组成一个集合 (2)不正确由于=,引=2由集合中元素的互异性知,这 个集合是由1,这3个元素组成的. (3)正确.集合中的元素相同,只是顺序不同,所以它们组成的集 合是相等的
导航 解:(1)不正确.因为“年轻人”没有确定的标准,对象不具有确定 性,所以不能组成一个集合. (3)正确.集合中的元素相同,只是顺序不同,所以它们组成的集 合是相等的. (2)不正确.由于𝟑 𝟐 = 𝟔 𝟒 , - 𝟏 𝟐 = 𝟏 𝟐 ,由集合中元素的互异性知,这 个集合是由 1,𝟑 𝟐 , 𝟏 𝟐 这 3 个元素组成的

导 规律总结 判断一组对象能不能组成一个集合的依据及切入点 ()依据:元素的确定性是判断的依据.如果考察的对象是确定 的,那么它们就能组成一个集合,否则不能组成一个集合 (2)切入点:解答此类问题的切入点是集合元素的特征,即确定 性、互异性和无序性
导航 判断一组对象能不能组成一个集合的依据及切入点 (1)依据:元素的确定性是判断的依据.如果考察的对象是确定 的,那么它们就能组成一个集合,否则不能组成一个集合. (2)切入点:解答此类问题的切入点是集合元素的特征,即确定 性、互异性和无序性