
全程设计 第五章 三角函数 5.1 任意确和孤度制 5.1.1 任意角
第五章 三角函数 5.1 任意角和弧度制 5.1.1 任意角

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.任意角的概念 按照角的旋转方向,分为如下三类: 类型定义 正角一 条射线绕其端点按 方向旋转形成的角 负角一条射线绕其端点按 方向旋转形成的角 零角如果一条射线没有做任何旋转,就称它形成了一个
导航 课前·基础认知 1.任意角的概念 按照角的旋转方向,分为如下三类: 类型 定义 正角 一条射线绕其端点按 逆时针 方向旋转形成的角 负角 一条射线绕其端点按 顺时针 方向旋转形成的角 零角 如果一条射线没有做任何旋转,就称它形成了一个 零角

导航 这样,我们就把角的概念推广到了 ,如果两个角a,P 的旋转方向相同且旋转量相等,那么就称 ;设a,B是任 意两个角,我们规定,把角α的终边旋转角B,这时终边所对应的 角是 ;按不同方向旋转相同的量所成的两个角叫做
导航 这样,我们就把角的概念推广到了 任意角 ,如果两个角α,β 的旋转方向相同且旋转量相等,那么就称 α=β ;设α,β是任 意两个角,我们规定,把角α的终边旋转角β,这时终边所对应的 角是 α+β ;按不同方向旋转相同的量所成的两个角叫做 互为相反角

导 微点拨1用图象表示角时,箭头的方向体现角的正负,因此箭 头不能丢掉 可类比正负数的规定,理解正角、负角是用来表示具有相反 意义的旋转量,理解角的加、减运算
导航 微点拨1 用图象表示角时,箭头的方向体现角的正负,因此箭 头不能丢掉. 可类比正负数的规定,理解正角、负角是用来表示具有相反 意义的旋转量,理解角的加、减运算

导航 微判断(1)经过1小时,时针转过30°.(× 2)终边与始边重合的角是零角.(×) (3)小于0°的角是锐角.(×) 解析:1)因为是顺时针旋转,所以时针转过-30° (2)终边与始边重合的角是k360°(k∈Z), (3)锐角是指大于0°且小于90°的角
导航 微判断 (1)经过1小时,时针转过30° .( ) (2)终边与始边重合的角是零角.( ) (3)小于90°的角是锐角.( ) 解析:(1)因为是顺时针旋转,所以时针转过-30° . (2)终边与始边重合的角是k·360°(k∈Z). (3)锐角是指大于0°且小于90°的角. × × ×

导航 2.象限角 我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原 点重合,角的始边与x轴的非负半轴重合.那么,角的终边在第 几象限,就说这个角是 如果角的终边在 ,那么就认为这个角不属于任何一个象限
导航 2.象限角 我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原 点重合,角的始边与x轴的非负半轴重合.那么,角的终边在第 几象限,就说这个角是 第几象限角 .如果角的终边在 坐标轴上 ,那么就认为这个角不属于任何一个象限
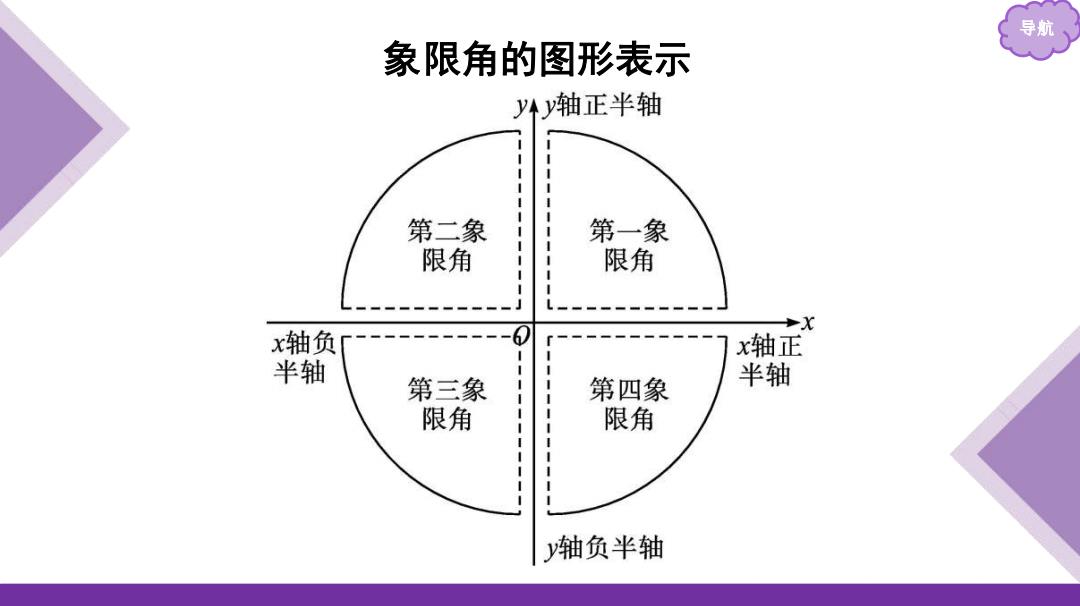
导航 象限角的图形表示 y4y轴正半轴 第二象 第一象 限角 限角 X x轴负 x轴正 半轴 第三象 第四象 半轴 限角 限角 y轴负半轴
导航 象限角的图形表示

导航 微训练1下列叙述正确的是( A.三角形的内角是第一象限角或第二象限角 B钝角是第二象限角 C第二象限角比第一象限角大 D.不相等的角终边一定不同 答案:B 解析:由于直角不属于任何一个象限,故A中叙述不正确;钝角在 90°~180°范围内且不为90°,180°,是第二象限角,故B中叙述正确; 由于120°是第二象限角,390°是第一象限角,但120°<390°,故C中叙 述不正确;由于20°与(360°+20)不相等,但终边相同,故D中叙述不 正确.故选B
导航 微训练1 下列叙述正确的是( ) A.三角形的内角是第一象限角或第二象限角 B.钝角是第二象限角 C.第二象限角比第一象限角大 D.不相等的角终边一定不同 答案:B 解析:由于直角不属于任何一个象限,故A中叙述不正确;钝角在 90° ~180°范围内且不为90°,180° ,是第二象限角,故B中叙述正确; 由于120°是第二象限角,390°是第一象限角,但120°<390° ,故C中叙 述不正确;由于20°与(360°+20°)不相等,但终边相同,故D中叙述不 正确.故选B

导航 3.终边相同的角 般地,我们有:所有与角终边相同的角,连同角α在内,可构 成一个集合S={BB=a+k360°,k∈Z,即任一与角终边相同的 角,都可以表示成角a与整数个 和
导航 3.终边相同的角 一般地,我们有:所有与角α终边相同的角,连同角α在内,可构 成一个集合S={β|β=α+k·360° ,k∈Z},即任一与角α终边相同的 角,都可以表示成角α与整数个 周角 的和