
全程设计 第五章 三角函数 5.1 任意角和弧度制 5.1.2 孤度制
第五章 三角函数 5.1 任意角和弧度制 5.1.2 弧度制

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1,角度制与弧度制 1)角度制和弧度制 用 作为单位来度量角的单位制叫做角度制规 角度制 定1度的角等于周角的60 我们规定,长度等于 的圆弧所对的 弧度制 叫做1弧度的角,弧度单位用符号rad表示, 读作
导航 课前·基础认知 1.角度制与弧度制 (1)角度制和弧度制 角度制 用 度 作为单位来度量角的单位制叫做角度制.规 定1度的角等于周角的 弧度制 我们规定,长度等于 半径长 的圆弧所对的 圆心角 叫做1弧度的角,弧度单位用符号rad表示, 读作 弧度 𝟏 𝟑𝟔𝟎

导 2)角的弧度数的计算 在半径为r的圆中,弧长为的弧所对的圆心角为arad,那么 la= 一 地,正角的弧度数是一个 ,负角的弧度数是一个 ,零角的弧度数是 微点拨1以孤度为单位表示角时,常常把孤度数写成多少π的 形式,若无特殊要求,则不必把π写成小数,如30°=石
导航 (2)角的弧度数的计算 在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么 |α|= . 一般地,正角的弧度数是一个 正数 ,负角的弧度数是一个 负数 ,零角的弧度数是 0 . 𝒍 𝒓 微点拨1以弧度为单位表示角时,常常把弧度数写成多少π的 形式,若无特殊要求,则不必把π写成小数,如30° = . 𝛑 𝟔

导航、 2.角度制与弧度制的换算 (1)角度与弧度的互化 角度化弧度 孤度化角度 360°= rad 2πrad= 180°= rad n rad= π rad≈ rad 180 rad-(9)°
导航 2 .角度制与弧度制的换算 (1)角度与弧度的互化 角度化弧度 弧度化角度 360°= 2 π rad 2 π rad = 360° 180°= π rad π rad = 180° 1°= 𝝅𝟏𝟖𝟎 rad ≈ 0.017 45 rad 1 rad = 𝟏 𝟖 𝟎 𝝅 °≈ 57.30°
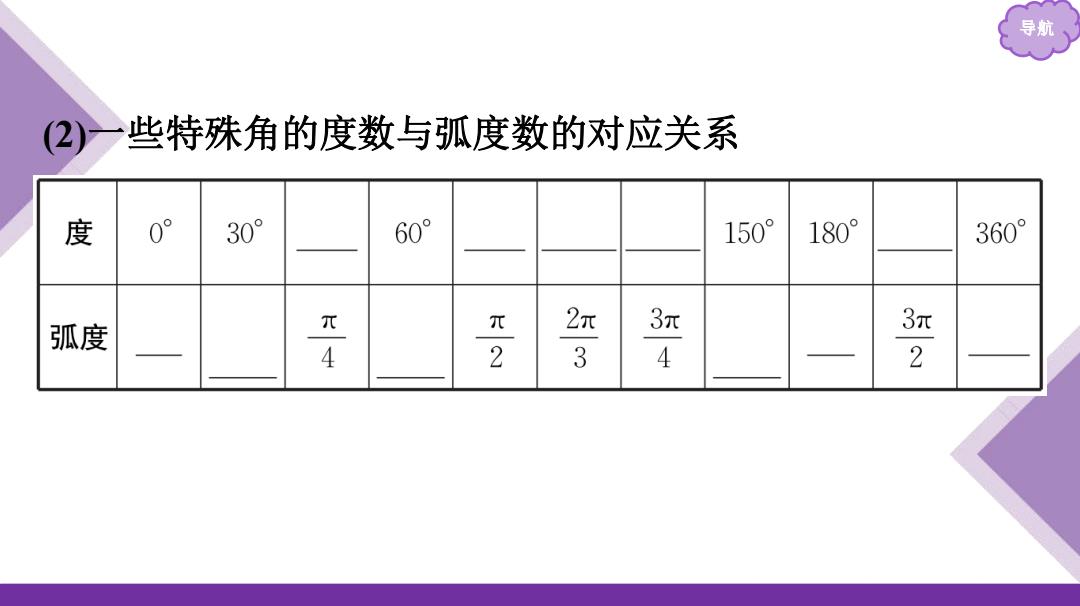
导航 (2) 些特殊角的度数与弧度数的对应关系 度 0° 30° 60° 150° 180° 360° 弧度 元 2元 3π 4 2 3 2
导航 (2)一些特殊角的度数与弧度数的对应关系

导航 微训练1用角度表示的结果为 ;135°用弧 度表示的结果为 答案:-300° 3π 4 解析:5受×(0)°-300; 5π_5 -135°=-135°×,m -3π 180° 4
导航 微训练 1 - 𝟓𝛑 𝟑 用角度表示的结果为 ;-135°用弧 度表示的结果为 . 答案:-300° - 𝟑𝛑 𝟒 解析:- 𝟓𝛑 𝟑 =- 𝟓𝛑 𝟑 × 𝟏𝟖𝟎 𝛑 °=-300°; -135°=-135°× 𝛑 𝟏𝟖𝟎° =- 𝟑𝛑 𝟒

导航 3.扇形的弧长及面积公式 设圆的半径为R,α为圆心角,1是扇形的弧长S是扇形的面积, 则 度量单位 角度制(0°<a<360°) 弧度制(0<α<2π) 扇形的弧长 扇形的面积
导航 3.扇形的弧长及面积公式 设圆的半径为R,α为圆心角,l是扇形的弧长,S是扇形的面积, 则

微点拨2(1)设圆的半径为R,α为圆心角,1是扇形的孤长,S是扇 形的面积,由弧长公式、扇形面积公式可知,已知,R,l,S中的 任意两个量可以求出另外两个量 (②)运用孤度制下的孤长公式和扇形面积公式明显比角度制 下的孤长公式和扇形面积公式要简单得多.扇形的弧长公式 I=aR及面积公式S-R=2R2(0<a<2m)中的u都是弧度数,应 用时必须将角度化为孤度, (3)在运用公式时,还应熟练掌握这两个公式的变形: ①urRR-②a30<as2m
导航 微点拨2(1)设圆的半径为R,α为圆心角,l是扇形的弧长,S是扇 形的面积,由弧长公式、扇形面积公式可知,已知α,R,l,S中的 任意两个量可以求出另外两个量. (2)运用弧度制下的弧长公式和扇形面积公式明显比角度制 下的弧长公式和扇形面积公式要简单得多.扇形的弧长公式 l=αR及面积公式S= lR= αR2 (0<α<2π)中的α都是弧度数,应 用时必须将角度化为弧度. (3)在运用公式时,还应熟练掌握这两个公式的变形: 𝟏 𝟐 𝟏 𝟐 ①α= 𝒍 𝑹 ,R=𝒍 𝜶 ;②α= 𝟐𝑺 𝑹 𝟐 (0<α<2π)

导 微训练2已知扇形的半径为20cm,圆心角为30°,则扇形的弧 长和面积S分别为 答案9 cm 100π cm2 3 解析:已知扇形的半径R=20cm,圆心角a=30°令 所以=aR-gx2-190 cm.S-JR-×19gx20-2100em2
导航 微训练2 已知扇形的半径为20 cm,圆心角为30° ,则扇形的弧 长l和面积S分别为 、 . 答案: 𝟏𝟎𝛑 𝟑 cm 𝟏𝟎𝟎𝛑 𝟑 cm2 解析:已知扇形的半径 R=20 cm,圆心角 α=30°= 𝛑 𝟔 , 所以 l=αR=𝛑 𝟔 ×20= 𝟏𝟎𝛑 𝟑 (cm),S=𝟏 𝟐 lR=𝟏 𝟐 × 𝟏𝟎𝛑 𝟑 ×20= 𝟏𝟎𝟎𝛑 𝟑 (cm2 )