
全程设计 第五章 三角函数 5.5三角恒等变换 5.5.2 简单的三角恒等变换
第五章 三角函数 5.5 三角恒等变换 5.5.2 简单的三角恒等变换

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 半角公式 sin 9
导航 课前 ·基础认知 半角公式 sin 𝜶𝟐 = ± 𝟏-𝐜 𝐨𝐬𝜶 𝟐 , cos 𝜶𝟐 = ± 𝟏 + 𝐜 𝐨𝐬𝜶 𝟐 , tan 𝜶𝟐 = ± 𝟏-𝐜 𝐨𝐬𝜶 𝟏 + 𝐜 𝐨𝐬𝜶

导航 因为不同的三角函数式不仅会有结构形式方面的差异,而且 还会存在所包含的角,以及这些角的三角函数种类方面的差 异,所以进行三角恒等变换时,常常要先寻找式子所包含的各 个角之间的联系,并以此为依据选择适当的公式,这是 的一个重要特点
导航 因为不同的三角函数式不仅会有结构形式方面的差异,而且 还会存在所包含的角,以及这些角的三角函数种类方面的差 异,所以进行三角恒等变换时,常常要先寻找式子所包含的各 个角之间的联系,并以此为依据选择适当的公式,这是 三角恒等变换 的一个重要特点
导 微点拨()若没有给出限定符号的条件,则在根号前保留正、 负号; (2)若给出角α所在的象限,则根据下表判定符号: a a a sin c0s tan z 第一象限 第一、三象限 +、- 十、- + 第二象限 第一、三象限 +、- 十、- + 第三象限 第二、四象限 十、- -、十 第四象限 第二、四象限 +、- -、+
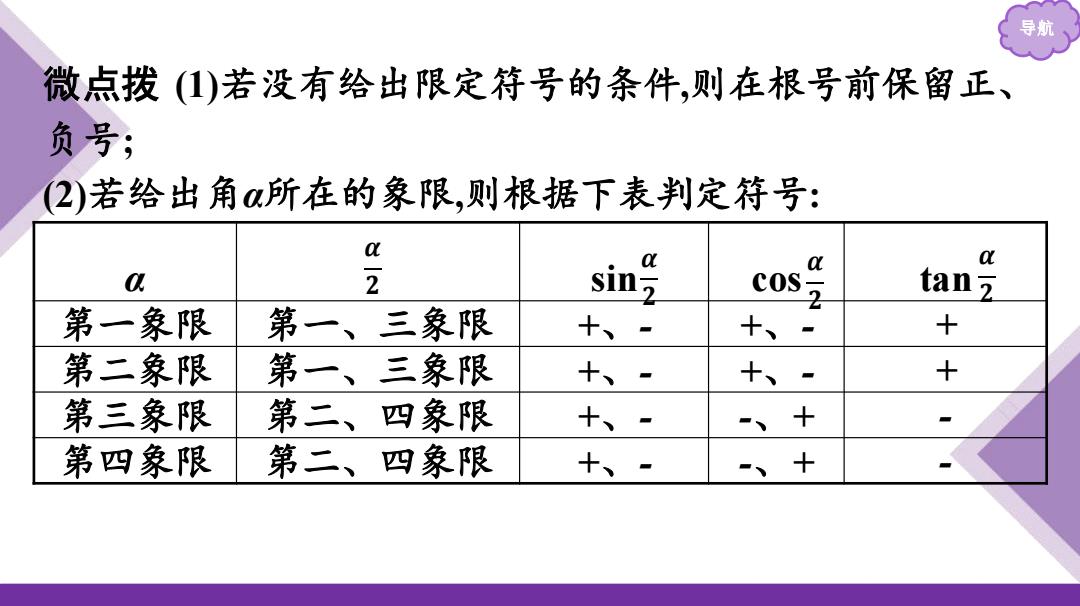
导航 微点拨 (1)若没有给出限定符号的条件,则在根号前保留正、 负号; (2)若给出角α所在的象限,则根据下表判定符号: α sin cos tan 第一象限 第一、三象限 +、- +、- + 第二象限 第一、三象限 +、- +、- + 第三象限 第二、四象限 +、- -、+ - 第四象限 第二、四象限 +、- -、+ - 𝜶 𝟐 𝜶 𝟐 𝜶 𝟐 𝜶 𝟐
导航 微判断 (1)半角公式适用于任意角. (×) 1-C0s30° (2)sin15°=±、 2 (X) (3)c0s = 1+C0S0 2 (X (4)若角a是第一象限角,则ta吃 1-cosa = \1+cosa
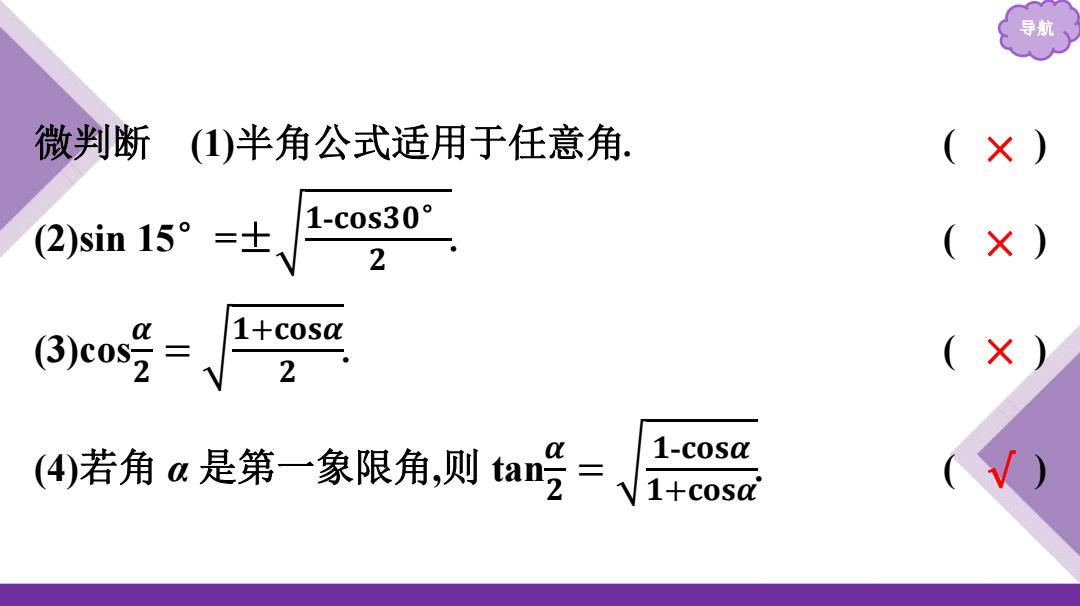
导航 微判断 (1)半角公式适用于任意角. ( ) (2)sin 15°=± 𝟏-𝐜𝐨𝐬𝟑𝟎° 𝟐 . ( ) (3)cos𝜶 𝟐 = 𝟏+𝐜𝐨𝐬𝜶 𝟐 . ( ) (4)若角 α 是第一象限角,则 tan𝜶 𝟐 = 𝟏-𝐜𝐨𝐬𝜶 𝟏+𝐜𝐨𝐬𝜶 . ( ) × × × √

导航 微训练已知cosu号a∈(受,2m,则a等于 答案号 解析:ra∈(z,2m)∈(m 4 又c0suF 4 1-c0S0 1 4 1十 3
导航 微训练 已知 cos α= 𝟒 𝟓 ,α∈ 𝟑𝛑 𝟐 ,𝟐𝛑 ,则 tan𝜶 𝟐 等于 . 答案:- 𝟏 𝟑 解析:∵α∈ 𝟑𝛑 𝟐 ,𝟐𝛑 ,∴ 𝜶 𝟐 ∈ 𝟑𝛑 𝟒 ,𝛑 . 又 cos α= 𝟒 𝟓 , ∴tan𝜶 𝟐 =- 𝟏-𝐜𝐨𝐬𝜶 𝟏+𝐜𝐨𝐬𝜶 =- 𝟏- 𝟒 𝟓 𝟏+ 𝟒 𝟓 =- 𝟏 𝟑

导航 课堂·重难突破 利用半角公式求值 典例剖析 1.(诺sin0-g,53元则sin号 (2已知cos0石0∈(r2m,则sinteo号一 答案0)3 (2明
导航 课堂·重难突破 一 利用半角公式求值 典例剖析 1.(1)若 sin θ= 𝟑 𝟓 , 𝟓𝛑 𝟐 <θ<3π,则 sin𝜽 𝟐 = . (2)已知 cos θ=- 𝟕 𝟐𝟓 ,θ∈(π,2π),则 sin𝜽 𝟐 +cos 𝜽 𝟐 = . 答案:(1)- 𝟑√𝟏𝟎 𝟏𝟎 (2)𝟏 𝟓

导航 解桥::sin0,0<3me(,3), cos-v1-in6-专si号 /1-c0s0 3V10 2 10 29∈m,2m号e((G又cos石 ∴si吃 1-c0S0 4 2
导航 解析:(1)∵sin θ= 𝟑 𝟓 , 𝟓𝛑 𝟐 <θ<3π,∴ 𝜽 𝟐 ∈ 𝟓𝛑 𝟒 , 𝟑𝛑 𝟐 , cos θ=-√𝟏-𝐬𝐢𝐧𝟐 𝜽=- 𝟒 𝟓 ,∴sin𝜽 𝟐 =- 𝟏-𝐜𝐨𝐬𝜽 𝟐 =- 𝟑√𝟏𝟎 𝟏𝟎 . (2)∵θ∈(π,2π),∴ 𝜽 𝟐 ∈ 𝛑 𝟐 ,𝛑 ,又 cos θ=- 𝟕 𝟐𝟓 , ∴sin𝜽 𝟐 = 𝟏-𝐜𝐨𝐬𝜽 𝟐 = 𝟒 𝟓 ,cos 𝜽 𝟐 =- 𝟏+𝐜𝐨𝐬𝜽 𝟐 =- 𝟑 𝟓 ,∴sin𝜽 𝟐 +cos 𝜽 𝟐 = 𝟏 𝟓

导航 规律总结 利用半角公式求值的思路 ()看角:若已知三角函数式中的角是待求三角函数式中角的 两倍,则求解时常常借助半角公式求解」 (2)明范围:由于半角公式求值常涉及符号问题,因此求解时务 必依据角的范围,求出相应半角的范围
导航 利用半角公式求值的思路 (1)看角:若已知三角函数式中的角是待求三角函数式中角的 两倍,则求解时常常借助半角公式求解. (2)明范围:由于半角公式求值常涉及符号问题,因此求解时务 必依据角的范围,求出相应半角的范围