
全程设计 第四章 指数数与对数数 4.1指数 第1课时 n次方根的概念
第四章 指数函数与对数函数 4.1 指数 第1课时 n次方根的概念

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
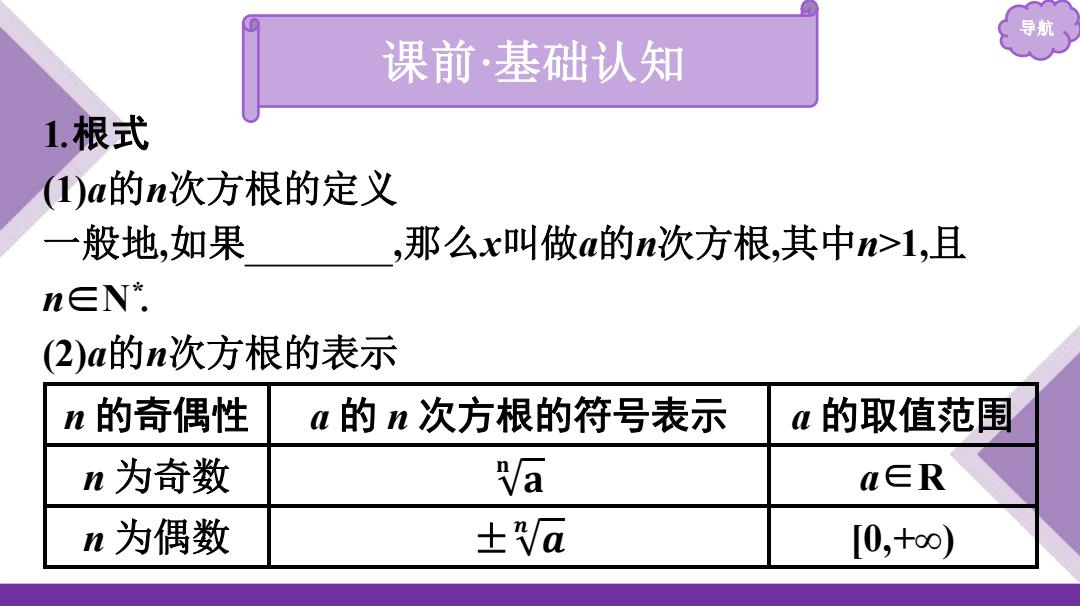
导航 课前·基础认知 1.根式 1)a的n次方根的定义 一般地,如果 ,那么x叫做a的n次方根,其中n>1,且 n∈N (2)a的n次方根的表示 n的奇偶性 a的n次方根的符号表示 a的取值范围 n为奇数 Va a∈R n为偶数 ±Va [0,+oo)
导航 课前·基础认知 1.根式 (1)a的n次方根的定义 一般地,如果 x n=a ,那么x叫做a的n次方根,其中n>1,且 n∈N* . (2)a的n次方根的表示 n 的奇偶性 a 的 n 次方根的符号表示 a 的取值范围 n 为奇数 𝐚 𝐧 a∈R n 为偶数 ± 𝒂 𝒏 [0,+∞)
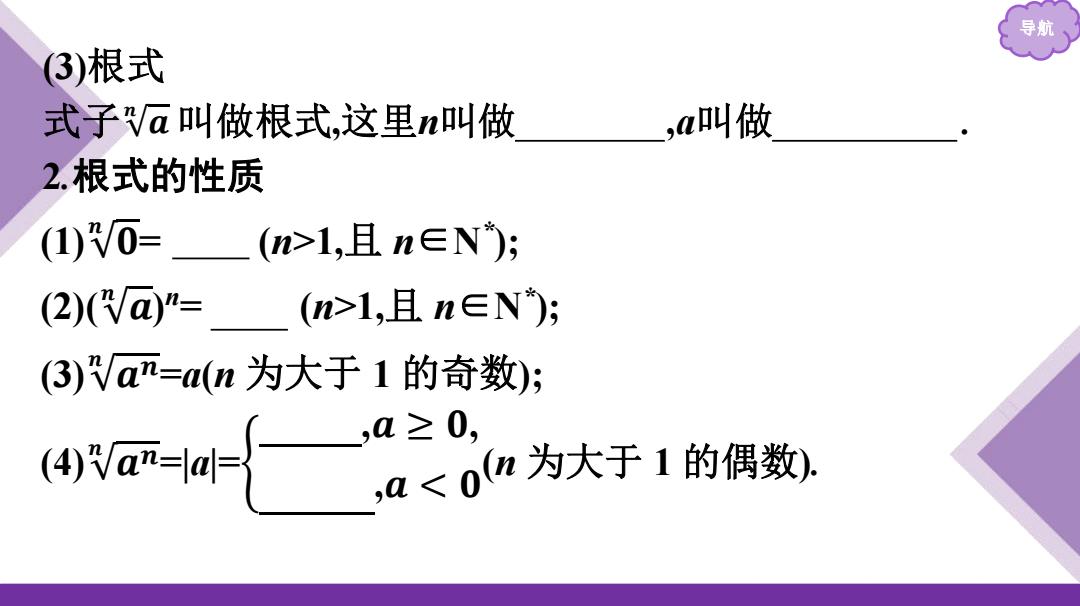
导航 3)根式 式子a叫做根式,这里n叫做 ,a叫做 2.根式的性质 (1)RV0=_(n>l,且n∈N; (2)(V@=(n>1,且n∈N); (3)Van=(n为大于1的奇数); a{加为大于1的得数
导航 (3)根式 式子 叫做根式,这里n叫做 根指数 ,a叫做 被开方数 . 2.根式的性质 𝒂 𝒏 (1) 𝟎 𝒏 = 0 (n>1,且 n∈N * ); (2)( 𝒂 𝒏 ) n = a (n>1,且 n∈N * ); (3)𝒏 𝒂𝒏 =a(n 为大于 1 的奇数); (4)𝒏 𝒂𝒏 =|a|= 𝒂 ,𝒂 ≥ 𝟎, -𝒂 ,𝒂 < 𝟎 (n 为大于 1 的偶数)

导航 微训练(若a-3-m3,、2-m则a+b的值为 A.1 B.5 C.-1 D.2π-5 2)下列说法:①-27-3,®81=±3,③(x+y)2=t+y 其中正确的是 (填序号) 答案:1)A2)③
导航 微训练 (1)若 a= (𝟑-𝝅) 𝟑 𝟑 ,b= (𝟐-𝛑) 𝟒 𝟒 ,则 a+b 的值为( ) A.1 B.5 C.-1 D.2π-5 (2)下列说法:① -𝟐𝟕 𝟑 =3;② 𝟖𝟏 𝟒 =±3;③ (𝒙 + 𝒚) 𝟐 =|x+y|. 其中正确的是 (填序号). 答案:(1)A (2)③

导 解标:(由根式的性质得3-n336-2-m4r2因 此+b=3-π)+π-2)=1. 故选A. (2)负数的奇次方根为负数,因而①中说法错误;⑧1是81的正 的4次方根,因而②中说法错误(化+y)是平方根,非负,因 而③中说法正确
导航 解析:(1)由根式的性质得 a= (𝟑-𝝅) 𝟑 𝟑 =3-π,b= (𝟐-𝛑) 𝟒 𝟒 =π-2,因 此 a+b=(3-π)+(π-2)=1. 故选 A. (2)负数的奇次方根为负数,因而①中说法错误; 𝟖𝟏 𝟒 是81的正 的 4 次方根,因而②中说法错误; (𝒙 + 𝒚) 𝟐 是平方根,非负,因 而③中说法正确

导航、 微思考根式化简开偶次方根时应注意什么问题? 提示:开偶次方根时,先用绝对值表示开方的结果,再去掉绝对 值号化简,化简时要结合条件或分类讨论
导航 微思考 根式化简开偶次方根时应注意什么问题? 提示:开偶次方根时,先用绝对值表示开方的结果,再去掉绝对 值号化简,化简时要结合条件或分类讨论

导航 课堂·重难突破 利用根式的性质化简或求值 典例剖析 1.化简: oj3oj-ow:
导航 课堂·重难突破 一 利用根式的性质化简或求值 典例剖析 1.化简: (1) (-𝟑) 𝟐 ; (2) (𝒂-𝒃) 𝟐 (a>b); (3) (-𝟒) 𝟒 𝟒 + (-𝛑) 𝟓 𝟓

导航 解:()-3)2-+3=3. ()(a-b)2=la-bl=a-b. B时40+m-4H网n
导航 解:(1) (-𝟑) 𝟐 =|-3|=3. (2) (𝒂-𝒃) 𝟐 =|a-b|=a-b. (3) (-𝟒) 𝟒 𝟒 + (-𝛑) 𝟓 𝟓 =|-4|+(-π)=4-π

导航 规律总结 当n(n>1)为奇数时,(Va"=Van=,a为任意实数均可;当n(n>1 为偶数时,a≥0,(Va)才有意义,且(代V@"=,而M为任意实 数,Van均有意义,且Van=a
导航 当n(n>1)为奇数时,( 𝐚 𝒏 ) n = 𝒏 𝒂𝒏 =a,a为任意实数均可;当n(n>1) 为偶数时,a≥0,( 𝒂 𝒏 ) n 才有意义,且( 𝒂 𝒏 ) n =a,而 a 为任意实 数, 𝒏 𝒂𝒏 均有意义,且 𝒏 𝒂𝒏 =|a|