
全程设计 第四章 指数数与对数数 4.2指数函数 第2课时 指数函数的图象与性质
第四章 指数函数与对数函数 4.2 指数函数 第2课时 指数函数的图象与性质

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
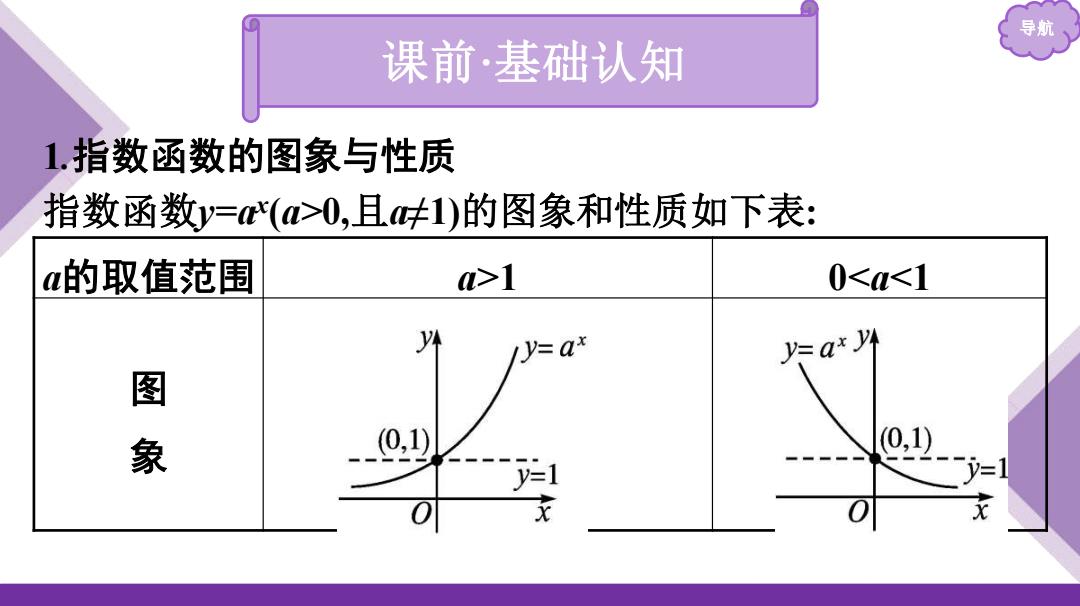
导航 课前·基础认知 1.指数函数的图象与性质 指数函数y=(>0,且呋1)的图象和性质如下表: a的取值范围 a>1 0<<1 Iy=ax y=axy 图 象 ,1) -0 (0,1) y=1 -y=1
导航 课前·基础认知 1.指数函数的图象与性质 指数函数y=ax (a>0,且a≠1)的图象和性质如下表: a的取值范围 a>1 0<a<1 图 象
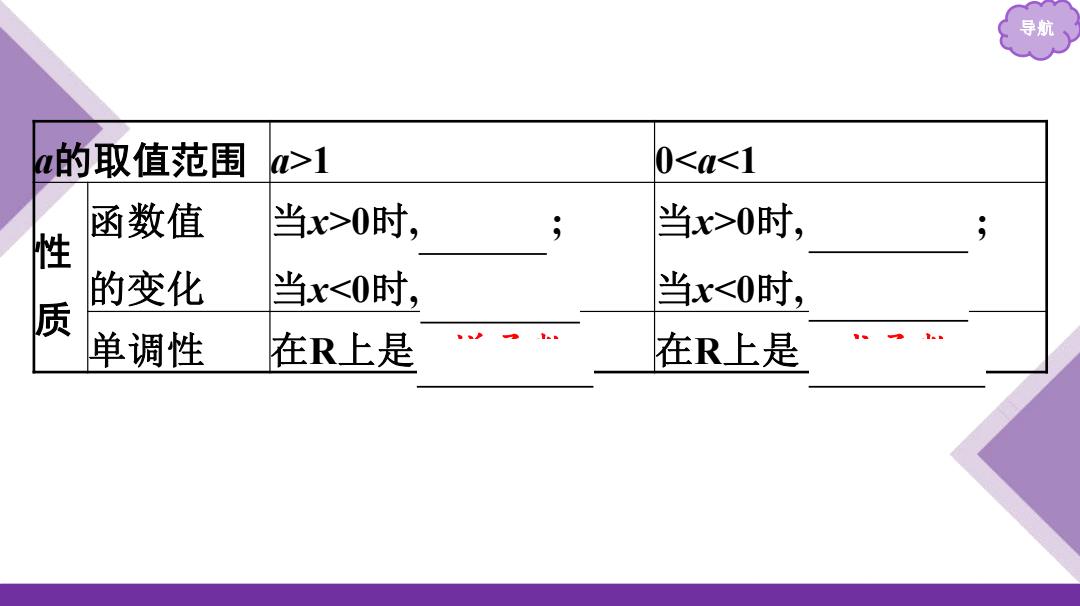
导航 的取值范围 a>1 00时, 当x>0时, ; 性 的变化 当x<0时, 当x<0时, 质 单调性 在R上是 在R上是
导航 a的取值范围 a>1 00时, y>1 ; 当x0时, 01 单调性 在R上是 增函数 在R上是 减函数
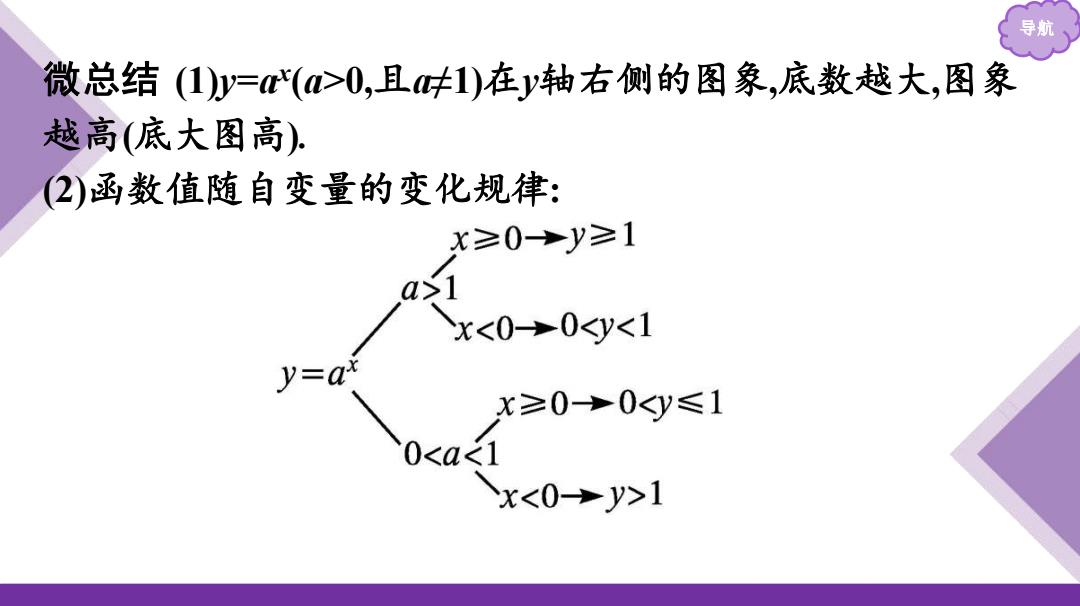
导航 微总结(1)y=(>0,且呋1)在y轴右侧的图象,底数越大,图象 越高(底大图高) 2)函数值随自变量的变化规律: x≥0→y≥1 a>1 x1
导航 微总结 (1)y=ax (a>0,且a≠1)在y轴右侧的图象,底数越大,图象 越高(底大图高). (2)函数值随自变量的变化规律:

导航 2.解指数方程、不等式 (1)形如aw>aw的不等式,可借助y=的 求解; (2)形如>b的不等式,可先将b化为以a为底数的指数幂的形 式,再借助y=的 求解; (3)形如br的不等式,可借助函数y=心与y=br的图象求解
导航 2.解指数方程、不等式 (1)形如a f(x)>ag(x)的不等式,可借助y=ax的 单调性 求解; (2)形如a f(x)>b的不等式,可先将b化为以a为底数的指数幂的形 式,再借助y=ax的 单调性 求解; (3)形如a x>bx的不等式,可借助函数y=ax与y=bx的图象求解

导航 微训练(1)若2+10,且呋1),且-2)>f-3),则a的取值范围 是 答案:1)D(2)0,1) 解析:(1).2x+1心3,'.0<<1
导航 微训练 (1)若2 x+10,且a≠1),且f(-2)>f(-3),则a的取值范围 是 . 答案:(1)D (2)(0,1) 解析:(1)∵2 x+1f(-3), 即a 2>a3 ,∴0<a<1

3.与指数函数复合的函数单调性 一 般地,形如y=w(>0,且呋1)的函数的性质有 ()函数y=w与函数y=fx)有 的定义域 (2)当>1时,函数y=w与y=fx)的单调性 ;当00,且呋1)的函数的单调性? 提示:1)定义法,即“取值一作差一变形一定号”.其中,在定号 过程中需要用到指数函数的单调性;(2)利用复合函数的单调 性“同增异减”的规律
导航 3.与指数函数复合的函数单调性 一般地,形如y=af(x) (a>0,且a≠1)的函数的性质有 (1)函数y=af(x)与函数y=f(x)有 相同 的定义域. (2)当a>1时,函数y=af(x)与y=f(x)的单调性 相同 ;当00,且a≠1)的函数的单调性? 提示:(1)定义法,即“取值—作差—变形—定号” .其中,在定号 过程中需要用到指数函数的单调性;(2)利用复合函数的单调 性“同增异减”的规律

导航 课堂·重难突破 利用函数的单调性比较大小 典例剖析 1.比较下列几组值的大小: 0-2.5与-25(2))与0.4 2 4 3 3⑤)产与()7,40.425与256
导航 课堂·重难突破 一 利用函数的单调性比较大小 典例剖析 1.比较下列几组值的大小: (1)(-2.5) 𝟐 𝟑与(-2.5) 𝟒 𝟓;(2) 𝟐 𝟓 - 𝟏 𝟐 与 0.𝟒 - 𝟑 𝟐; (3) 𝟏 𝟑 - 𝟏 𝟐 与 𝟑 𝟐 - 𝟏 𝟐 ;(4)0.4 -2.5 与 2.5 1.6

导航 2 解:(山)由于(2.5)=2.5,(2.5)5=2.55,函数y=2.5为增函数, 4 4 4 二3 5 2 4 因而(-2.5)<(-2.5) 3 2由于Q42=()产,画教)为减函数, 3 又因而(目之4
导航 解:(1)由于(-2.5) 𝟐 𝟑=2.𝟓 𝟐 𝟑,(-2.5) 𝟒 𝟓=2.𝟓 𝟒 𝟓,函数 y=2.5 x 为增函数, 又 𝟐 𝟑 < 𝟒 𝟓 , 因而(-2.5) 𝟐 𝟑<(-2.5) 𝟒 𝟓. (2)由于 0.𝟒 - 𝟑 𝟐 = 𝟐 𝟓 - 𝟑 𝟐 ,函数 y= 𝟐 𝟓 𝒙 为减函数, 又- 𝟑 𝟐 <- 𝟏 𝟐 ,因而 𝟐 𝟓 - 𝟏 𝟐 <0.𝟒 - 𝟑 𝟐