
全程设计 第五章 ,三角虽数 5.2三角函数的概念 5.2.1三角函数的概念 第2课时 三角函数值的符号及诱导公式一
第五章 三角函数 5.2 三角函数的概念 5.2.1 三角函数的概念 第2课时 三角函数值的符号及诱导公式一

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
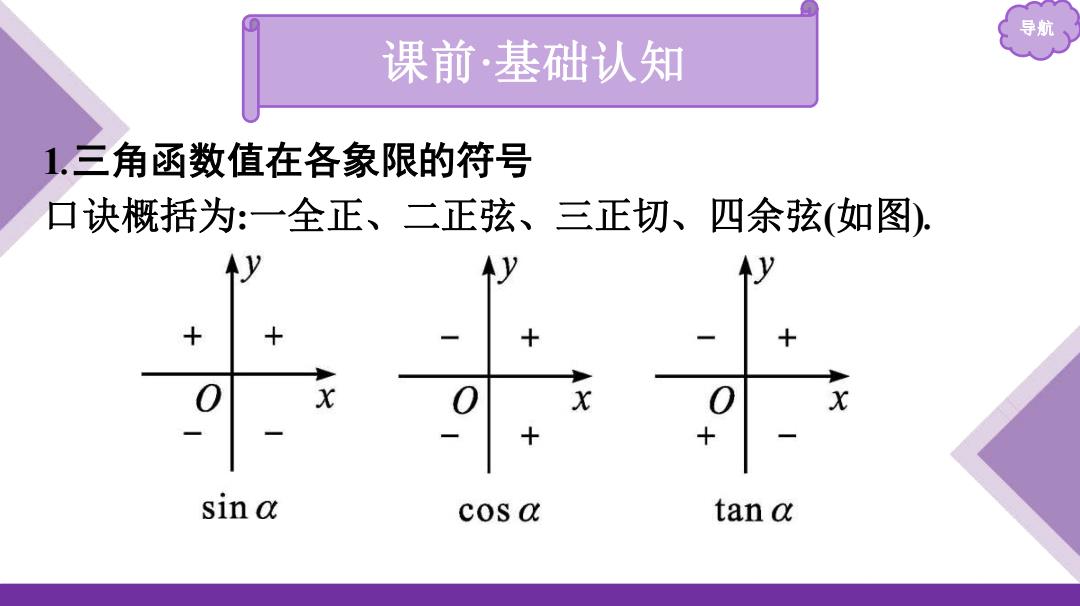
导航 课前·基础认知 1,三角函数值在各象限的符号 口诀概括为:一全正、二正弦、三正切、四余弦(如图) X X sin a cos a tan q
导航 课前·基础认知 1.三角函数值在各象限的符号 口诀概括为:一全正、二正弦、三正切、四余弦(如图)

导航 微点拨1(1)正弦值的符号由纵坐标y的符号确定; (2)余弦值的符号由横坐标x的符号确定; 3)正切值的符号由纵坐标y、横坐标x的符号共同确定,且同 号为正,异号为负
导航 微点拨1 (1)正弦值的符号由纵坐标y的符号确定; (2)余弦值的符号由横坐标x的符号确定; (3)正切值的符号由纵坐标y、横坐标x的符号共同确定,且同 号为正,异号为负

导航 微训练1若-2<a<0,则点(tana,cosa)位于( A.第一象限B.第二象限 C,第三象限D.第四象限 答案:B 解析:受a<0,∴tana<0,cosa心0, ∴点(tana,cosa位于第二象限
导航 微训练1 若- 0, ∴点(tan α,cos α)位于第二象限. 𝛑 𝟐 𝛑 𝟐

导 2.诱导公式一 ()语言表示:终边相同的角的 三角函数的值相等 (2)式子表示: sin(c+k2π)= C0S(a+k2π)= tan(a+k2π)= ,其中k∈Z. 利用公式一,可以把求任意角的三角函数值,转化为求0~2π (或0°~360)角的三角函数值
导航 2.诱导公式一 (1)语言表示:终边相同的角的 同一 三角函数的值相等. (2)式子表示: 𝐬𝐢𝐧(𝜶 + 𝒌·𝟐𝛑) = 𝐬𝐢𝐧𝜶 , 𝐜𝐨𝐬(𝜶 + 𝒌·𝟐𝛑) = 𝐜𝐨𝐬𝜶 , 𝐭𝐚𝐧(𝜶 + 𝒌·𝟐𝛑) = 𝐭𝐚𝐧𝜶 ,其中𝒌∈𝐙. 利用公式一,可以把求任意角的三角函数值,转化为求0~2π (或0° ~360°)角的三角函数值

导航、 微点拨2三角函数值有“周而复始”的变化规律,角的终边每 绕原点旋转一周,函数值将重复出现
导航 微点拨2 三角函数值有“周而复始”的变化规律,角α的终边每 绕原点旋转一周,函数值将重复出现
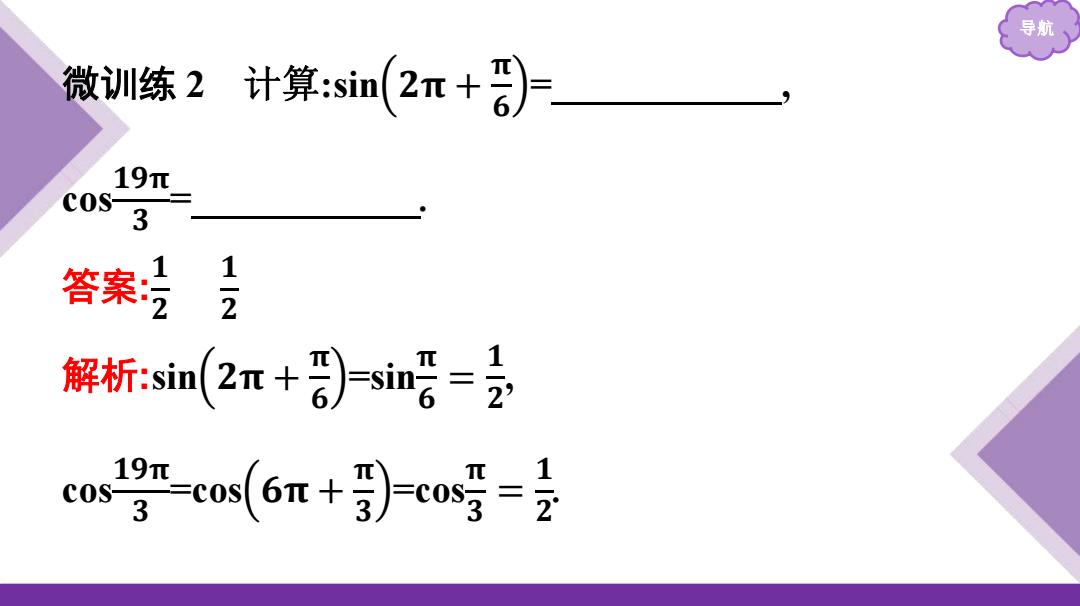
导航 微训练2计算:sin(2π+君) 19r= cos 3 答案吃司 解析:sin(2m+引-sing=会 co29π-c0s(6m+罗}-cos号=2
导航 微训练 2 计算:sin 𝟐𝛑 + 𝛑 𝟔 = , cos 𝟏𝟗𝛑 𝟑 = . 答案: 𝟏 𝟐 𝟏 𝟐 解析:sin 𝟐𝛑 + 𝛑 𝟔 =sin𝛑 𝟔 = 𝟏 𝟐 , cos 𝟏𝟗𝛑 𝟑 =cos 𝟔𝛑 + 𝛑 𝟑 =cos 𝛑 𝟑 = 𝟏 𝟐

导航 课堂·重难突破 三角函数值符号的判断 典例剖析 1.已知角A为第三象限角,且sin引sin2则角号是第 象限角. 答案:四
导航 课堂·重难突破 一 三角函数值符号的判断 典例剖析 1.已知角 A 为第三象限角,且 𝐬𝐢𝐧 𝑨 𝟐 =-sin𝑨 𝟐 ,则角𝑨 𝟐 是第 象限角. 答案:四

导航 解析:角A为第三象限角,为第二或第四象限角 又sin引=sin2si吃0, 角为第四象限角
导航 解析:∵角 A 为第三象限角,∴ 𝑨 𝟐 为第二或第四象限角. 又 𝐬𝐢𝐧 𝑨 𝟐 =-sin𝑨 𝟐 ,∴sin𝑨 𝟐 <0, ∴角 𝑨 𝟐 为第四象限角