
全程设计 第五章 三角数 5.3 诱导公式 第1课时 三角函数的诱导公式二四
第五章 三角函数 5.3 诱导公式 第1课时 三角函数的诱导公式二~ 四

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 诱导公式二、三、四 (1)诱导公式二 终边关系 图示 角π+a与角a的终边 π+a P 关于 对称 P2 公式 sin(π+a)= C0S(π+)= ,tan(π+a=
导航 课前·基础认知 诱导公式二、三、四 (1)诱导公式二 终边关系 图示 角π+α与角α的终边 关于 原点 对称 公式 sin(π+α)= -sin α , cos(π+α)= -cos α ,tan(π+α)= tan α

导航 微点拨1记忆规律 把角看作锐角时不会影响诱导公式中右边式子前面的特号, 因此记忆公式符号时通常把角α看成锐角,则π+α是第三象限 角,函数名不变,符号为第三象限角的三角函数值的符号
导航 微点拨1 记忆规律 把角α看作锐角时不会影响诱导公式中右边式子前面的符号, 因此记忆公式符号时通常把角α看成锐角,则π+α是第三象限 角,函数名不变,符号为第三象限角的三角函数值的符号

导航 微训练1已知tana=4,则tan(π+a)等于( A.π+4 B.4 C.-4 D.4-元 答案:B 解析:tan(π+=tana=4
导航 微训练1 已知tan α=4,则tan(π+α)等于( ) A.π+4 B.4 C.-4 D.4-π 答案:B 解析:tan(π+α)=tan α=4
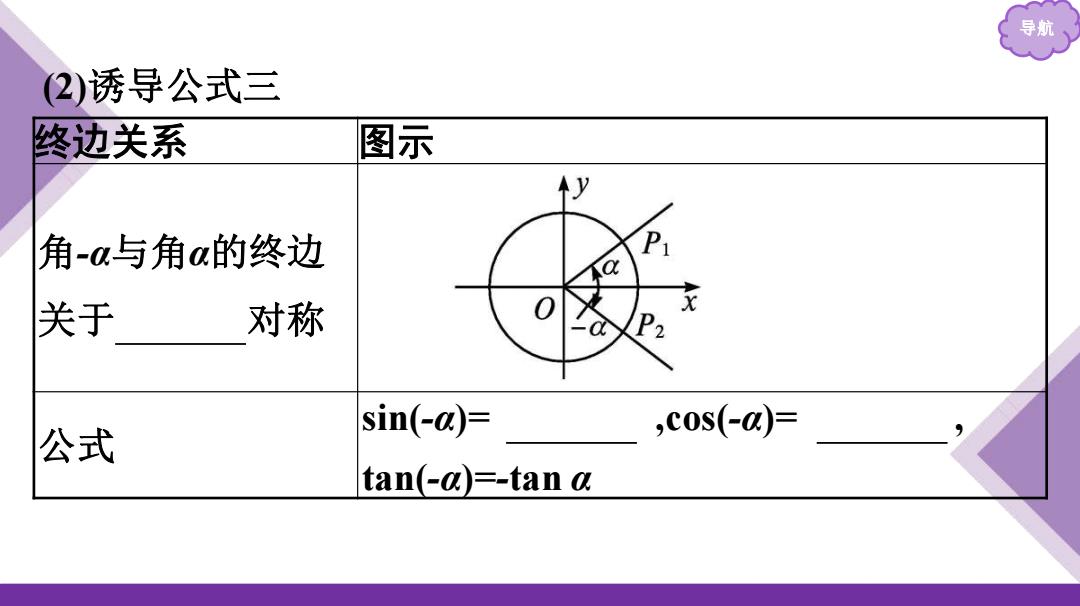
导航 2)诱导公式三 终边关系 图示 角-a与角a的终边 关于 对称 公式 sin(-a)= ,c0s(-a)= tan(-a)=-tan a
导航 (2)诱导公式三 终边关系 图示 角-α与角α的终边 关于 x轴 对称 公式 sin(-α)= -sin α ,cos(-α)= cos α , tan(-α)=-tan α

导航 微点拨2记忆规律 把角α看作锐角,则-α是第四象限角,函数名不变,符号为第四 象限角的三角函数值的符号
导航 微点拨2 记忆规律 把角α看作锐角,则-α是第四象限角,函数名不变,符号为第四 象限角的三角函数值的符号

导航 微训练2si如(君)+cos()的值是 答案 解桥:sin(-君)+cos(-)sing+cos5tos(π+) 1 π1+√2 =-2c0 42
导航 微训练 2 sin - 𝛑 𝟔 +cos - 𝟓𝛑 𝟒 的值是 . 答案:- 𝟏+ 𝟐 𝟐 解析:sin - 𝛑 𝟔 +cos - 𝟓𝛑 𝟒 =-sin𝛑 𝟔 +cos 𝟓𝛑 𝟒 =- 𝟏 𝟐 +cos 𝛑 + 𝛑 𝟒 =- 𝟏 𝟐 -cos 𝛑 𝟒 =- 𝟏+ 𝟐 𝟐
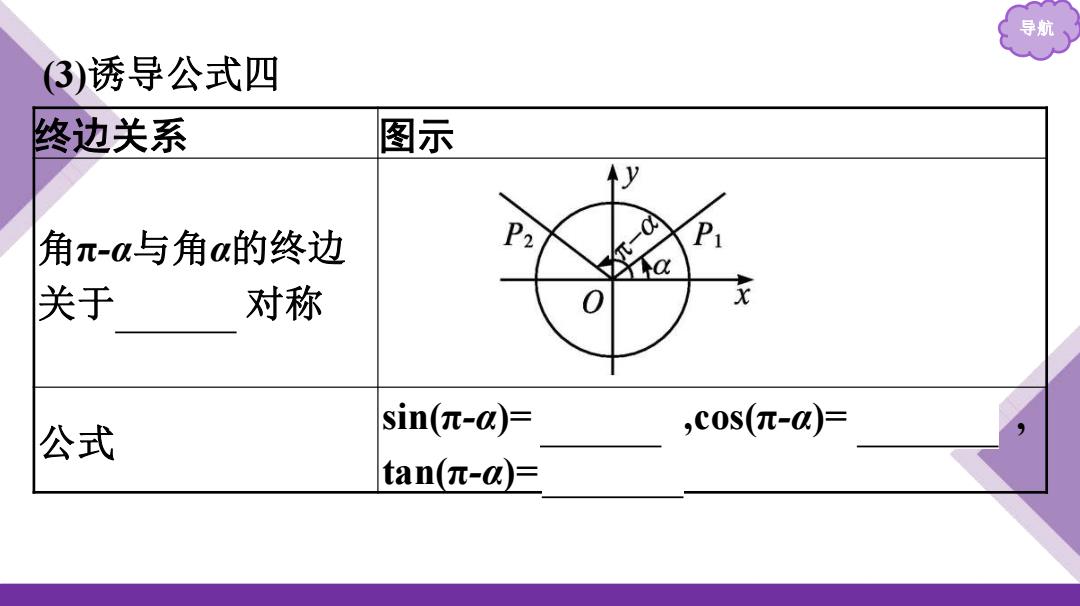
导航 3)诱导公式四 终边关系 图示 y 角π-a与角a的终边 P2 P 关于 对称 sin(π-d= 公式 ,C0s(π-☑)= tan(π-)=
导航 (3)诱导公式四 终边关系 图示 角π-α与角α的终边 关于 y轴 对称 公式 sin(π-α)= sin α ,cos(π-α)= -cos α , tan(π-α)= -tan α

导航、 微点拨3记忆规律 把α看作锐角,则π-a是第二象限角,三角函数名不变,符号为第 二象限角的三角函数值的符号
导航 微点拨3 记忆规律 把α看作锐角,则π-α是第二象限角,三角函数名不变,符号为第 二象限角的三角函数值的符号