
全程设计 第三章 函数的概念与性质 3.2 数的基本性质 3.2.2 奇偶性
第三章 函数的概念与性质 3.2 函数的基本性质 3.2.2 奇偶性

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.函数的奇偶性 奇偶性 偶函数 奇函数 一般地,设函数fx)的定义域为D,如果x∈D,都有 条件 x∈D 结论 f-x)=fx) f孔-x)=-f) 图象特点 关于 ·对称 关于 上 对称
导航 课前·基础认知 1.函数的奇偶性 奇偶性 偶函数 奇函数 条件 一般地,设函数f(x)的定义域为D,如果∀x∈D,都有 -x∈D 结论 f(-x)=f(x) f(-x)=-f(x) 图象特点 关于 y轴 对称 关于 原点 对称

导期 微提醒()奇偶性是函数的整体性质,所以判断函数的奇偶性 应先明确它的定义域对照函数的单调性是函数的局部性质, 以加深理解) (2)奇函数、偶函数的定义域关于原点对称,反之,若定义域不 关于原点对称,则这个函数一定不具有奇偶性
导航 微提醒 (1)奇偶性是函数的整体性质,所以判断函数的奇偶性 应先明确它的定义域(对照函数的单调性是函数的局部性质, 以加深理解). (2)奇函数、偶函数的定义域关于原点对称,反之,若定义域不 关于原点对称,则这个函数一定不具有奇偶性

导航 2.奇函数、偶函数的性质 )若一个奇函数在原点处有定义,即0)有意义,则一定有 f0)= 2)若fx)是奇函数,则fx)在其关于原点对称的区间上单调性 (3)若fx)是偶函数,则侧fx)在其关于原点对称的区间上单调性
导航 2.奇函数、偶函数的性质 (1)若一个奇函数在原点处有定义,即f(0)有意义,则一定有 f(0)= 0 . (2)若f(x)是奇函数,则f(x)在其关于原点对称的区间上单调性 一致 . (3)若f(x)是偶函数,则f(x)在其关于原点对称的区间上单调性 相反

导航 课堂·重难突破 函数奇偶性的判断 典例剖析 1.判断下列函数的奇偶性: (1n)2+,(2=3-2x 2x2+2x 3)fx)=Vx4+x2+1
导航 课堂·重难突破 一 函数奇偶性的判断 典例剖析 1.判断下列函数的奇偶性: (1)f(x)= 𝟐𝒙 𝟐 +𝟐𝒙 𝒙+𝟏 ;(2)f(x)=x3 -2x; (3)f(x)= 𝒙 𝟒 + 𝒙 𝟐 + 𝟏

解:1)函数的定义域为{x≠1,不关于原点对称,所以fx)既不 是奇函数也不是偶函数 (2)函数的定义域为R因为x∈R,都有x∈R,且 f-x)=(-x)3-2(-x)=-x3+2x=-(x3-2x)=-fx),所以函数fx)是奇函数 (3)函数的定义域为R因为x∈R,都有x∈R, 且-片(-x)4+(x2+1=Vx4+x2+1e, 所以函数fx)是偶函数
导航 解:(1)函数的定义域为{x|x≠-1},不关于原点对称,所以f(x)既不 是奇函数也不是偶函数. (2)函数的定义域为R.因为∀x∈R,都有-x∈R,且 f(-x)=(-x) 3 -2(-x)=-x 3+2x=-(x 3 -2x)=-f(x),所以函数f(x)是奇函数. (3)函数的定义域为R.因为∀x∈R,都有-x∈R, 所以函数f(x)是偶函数. 且 f(-x)= (-𝒙) 𝟒 + (-𝒙) 𝟐 + 𝟏 = 𝒙 𝟒 + 𝒙 𝟐 + 𝟏=f(x)
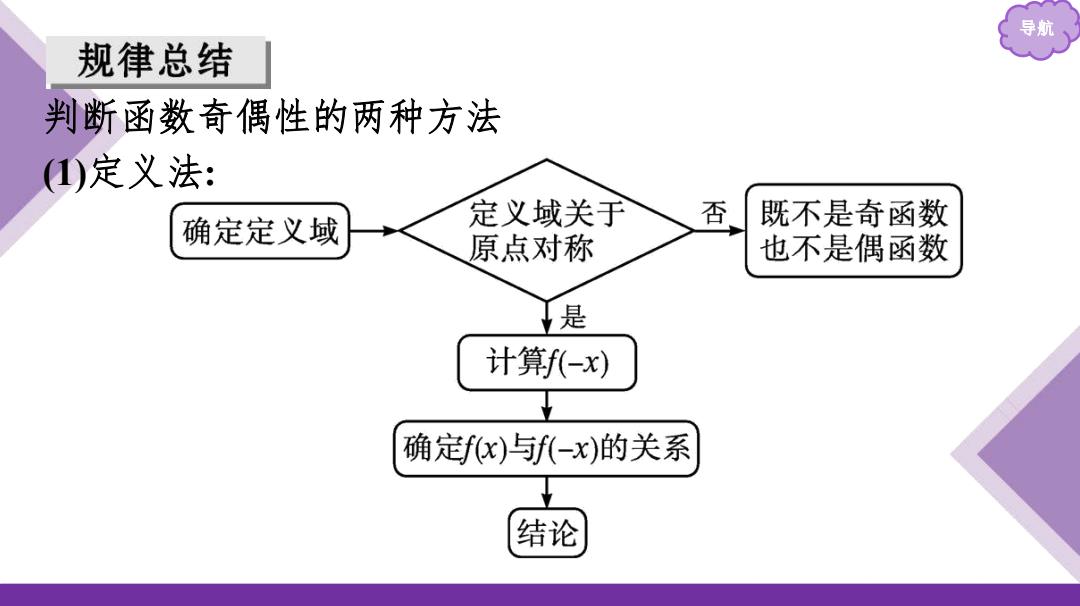
导航 规律总结 判断函数奇偶性的两种方法 )定义法: 否 确定定义域 定义域关于 既不是奇函数 原点对称 也不是偶函数 是 计算f孔-x) 确定fx)与f(-x)的关系 结论
导航 判断函数奇偶性的两种方法 (1)定义法 :
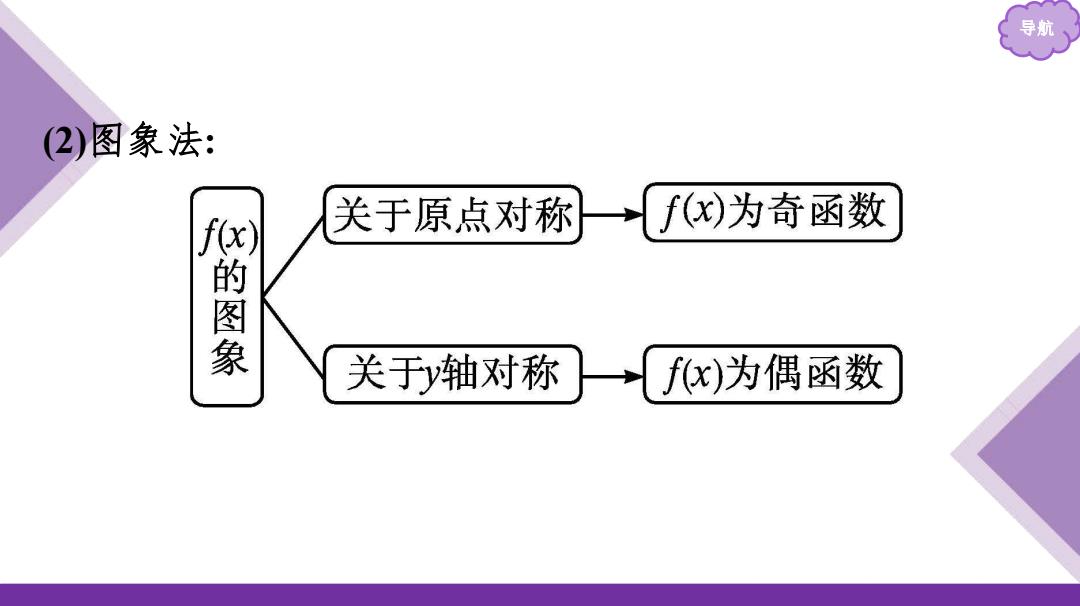
导航 (2)图象法: 关于原点对称 f(x)为奇函数 你的图象 关于y轴对称 fx)为偶函数
导航 (2)图象法:
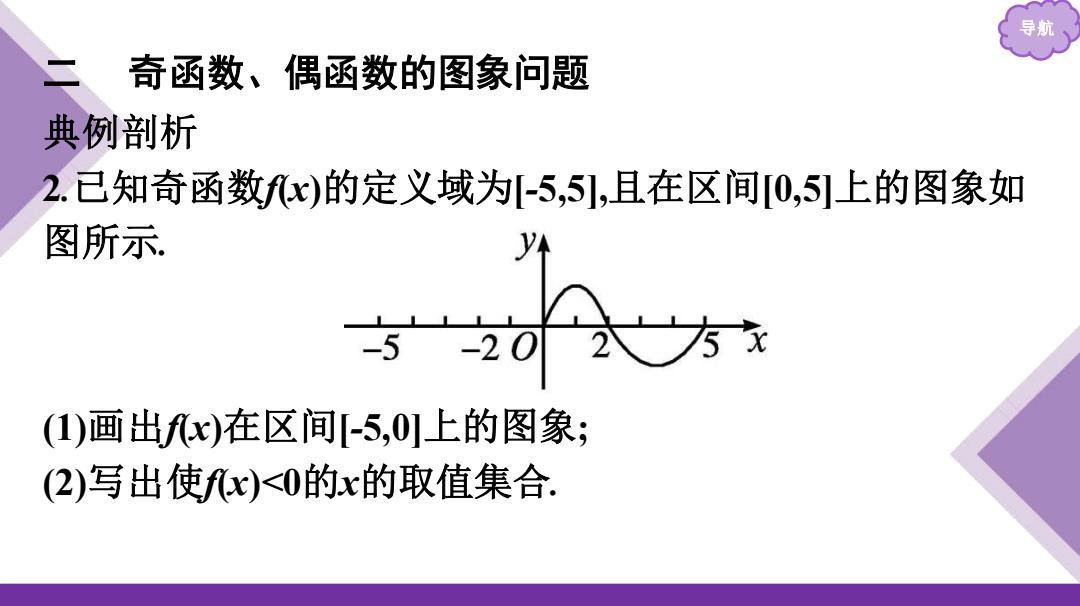
导 奇函数、偶函数的图象问题 典例剖析 2.已知奇函数fx)的定义域为[-5,5],且在区间[0,5]上的图象如 图所示 -20 (1)画出fx)在区间[-5,0]上的图象 (2)写出使fx)<0的x的取值集合
导航 二 奇函数、偶函数的图象问题 典例剖析 2.已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如 图所示. (1)画出f(x)在区间[-5,0]上的图象; (2)写出使f(x)<0的x的取值集合