
全程设计 第4课时 余弦定理、正弦定理应用举例
第4课时 余弦定理、正弦定理应用举例

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.基线的概念与选择原则 (1)定义 在测量过程中,把根据测量的需要而确定的 叫做基 线 (2)性质 在测量过程中,应根据实际需要选取合适的 ,使 测量具有较高的精确度.一般来说,基线越长,测量的精确度越
导航 课前·基础认知 1.基线的概念与选择原则 (1)定义 在测量过程中,把根据测量的需要而确定的 线段 叫做基 线. (2)性质 在测量过程中,应根据实际需要选取合适的基线长度 ,使 测量具有较高的精确度.一般来说,基线越长,测量的精确度越 高

导航 微思考1在测量距离的问题中,如果已知构造的三角形的 三个内角,那么能解出三角形的边长吗? 提示:不能,要解一个三角形,至少要知道这个三角形的一 条边的长度
导航 微思考1 在测量距离的问题中,如果已知构造的三角形的 三个内角,那么能解出三角形的边长吗? 提示:不能,要解一个三角形,至少要知道这个三角形的一 条边的长度
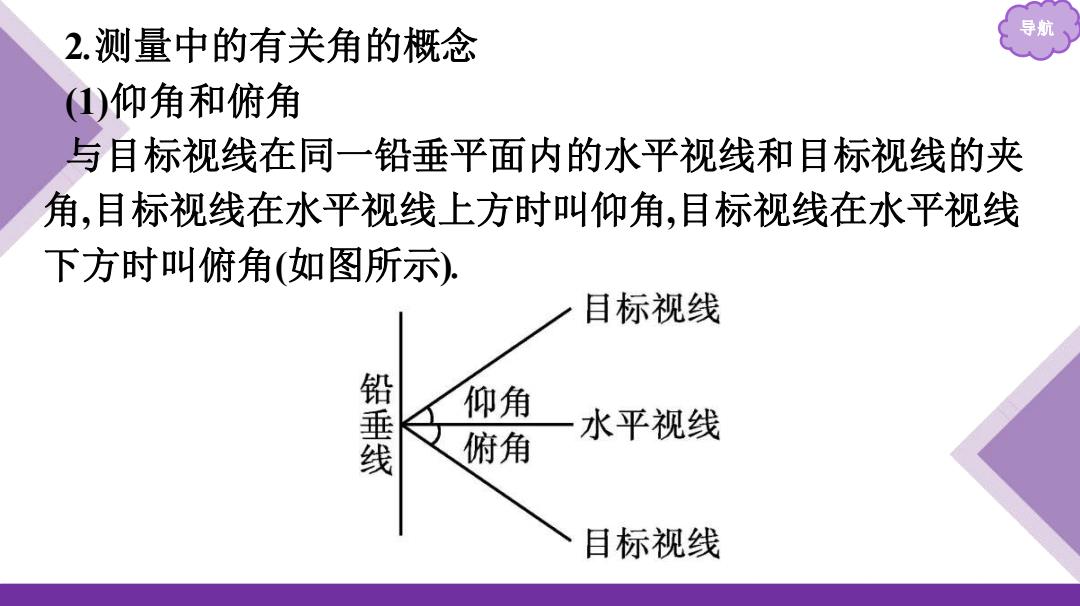
2.测量中的有关角的概念 导期 (1)仰角和俯角 与目标视线在同一铅垂平面内的水平视线和目标视线的夹 角,目标视线在水平视线上方时叫仰角,目标视线在水平视线 下方时叫俯角(如图所示) 目标视线 铅垂线 仰角 一水平视线 俯角 目标视线
导航 2.测量中的有关角的概念 (1)仰角和俯角 与目标视线在同一铅垂平面内的水平视线和目标视线的夹 角,目标视线在水平视线上方时叫仰角,目标视线在水平视线 下方时叫俯角(如图所示)

(2)方向角 导 从指定方向线到目标方向线所成的水平角.如南偏西60°,即以 正南方向为始边,顺时针方向向西旋转60°(如图所示) 北 西 目标方向线 60° 南 微思考2李尧出校向南前进了200米,再向东走了200米,回到自 己家中,你认为李尧的家在学校的哪个方向? 提示:东南方向
导航 (2)方向角 从指定方向线到目标方向线所成的水平角.如南偏西60° ,即以 正南方向为始边,顺时针方向向西旋转60°(如图所示). 微思考2 李尧出校向南前进了200米,再向东走了200米,回到自 己家中,你认为李尧的家在学校的哪个方向? 提示:东南方向

导航 3.解三角形实际问题 )解题思路 抽象概括 实际问题 数学模型 得以解决 推理运算 解三角形) 还原说明 实际问题的解 数学模型的解
导航 3 .解三角形实际问题 (1)解题思路

(2)基本步骤 利用正弦定理、余弦定理解决实际问题的基本步骤如下 ①分析:理解题意,弄清已知与未知,画出示意图(一个或几个 三角形). ②建模:根据已知条件与求解目标,把已知量与待求量尽可 能地集中在有关三角形中,建立一个解三角形的数学模型, ③求解:利用正弦定理、余弦定理解三角形,求得数学模型 的解. ④检验:检验所求的解是否符合实际问题,从而得出实际问 题的解
导航 (2)基本步骤 利用正弦定理、余弦定理解决实际问题的基本步骤如下 ①分析:理解题意,弄清已知与未知,画出示意图(一个或几个 三角形). ②建模:根据已知条件与求解目标,把已知量与待求量尽可 能地集中在有关三角形中,建立一个解三角形的数学模型. ③求解:利用正弦定理、余弦定理解三角形,求得数学模型 的解. ④检验:检验所求的解是否符合实际问题,从而得出实际问 题的解

导航 (3)主要类型 三角形中的几何计算问题的主要类型 长度问题 角度问题 面积问题 转化 转化 转化 三角形或其 三角形的边长 三角形的内角 他特殊图形 的面积 正弦定理、余弦定理 三角形面积公式
导航 (3)主要类型

导航 课堂·重难突破 测量距离问题 典例剖析 1.海上有A,B,C三个小岛,已知A,B两个小岛相距10海里,从A 岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视 角,则B,C间的距离是(D)海里. A.10v3 B.10v6 3 C.5V2 D.5V6
导航 课堂·重难突破 一 测量距离问题 典例剖析 1.海上有A,B,C三个小岛,已知A,B两个小岛相距10海里,从A 岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视 角,则B,C间的距离是( D )海里. A.10 𝟑 B. 𝟏𝟎 𝟔 𝟑 C.5 𝟐 D.5 𝟔