
全程设计 8.4.1 平面
8.4.1 平面

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导期 课前·基础认知 L.平面的概念 几何里所说的“平面”,是从课桌面、黑板面、平静的水面等 一些物体中抽象出来的.几何里的平面是向四周 的. 微思考1一个平面能否把空间分成两部分? 提示:因为平面是无限延展的,所以一个平面能把空间分成 两部分
导航 课前·基础认知 1.平面的概念 几何里所说的“平面”,是从课桌面、黑板面、平静的水面等 一些物体中抽象出来的.几何里的平面是向四周 无限延展 的. 微思考1 一个平面能否把空间分成两部分? 提示:因为平面是无限延展的,所以一个平面能把空间分成 两部分
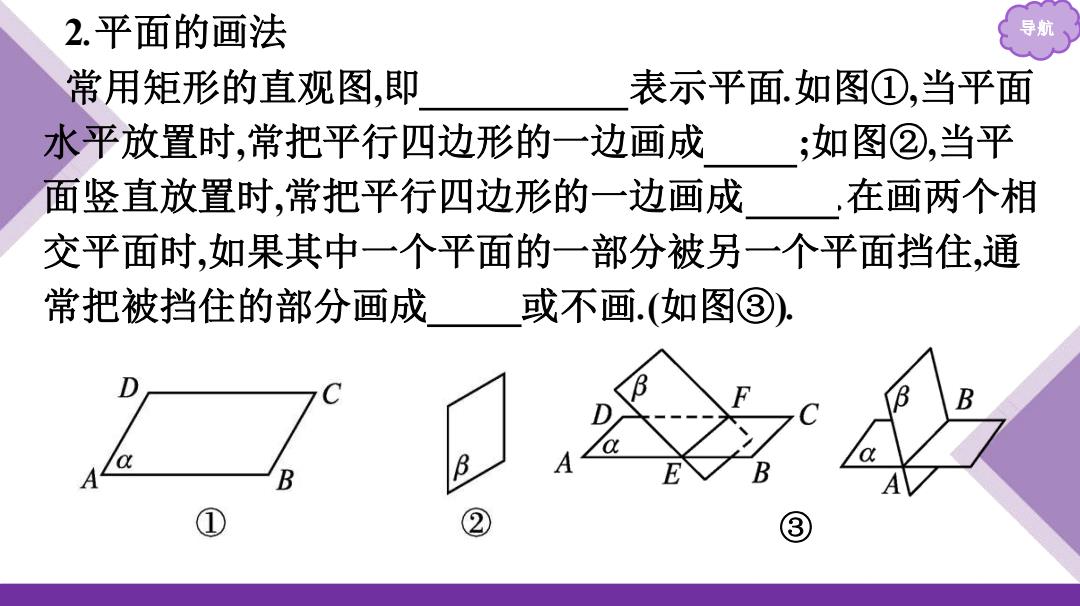
2.平面的画法 导期 常用矩形的直观图,即 表示平面.如图①,当平面 水平放置时,常把平行四边形的一边画成 ;如图②,当平 面竖直放置时,常把平行四边形的一边画成,在画两个相 交平面时,如果其中一个平面的一部分被另一个平面挡住,通 常把被挡住的部分画成 或不画.(如图③)
导航 2.平面的画法 常用矩形的直观图,即 平行四边形 表示平面.如图①,当平面 水平放置时,常把平行四边形的一边画成横向 ;如图②,当平 面竖直放置时,常把平行四边形的一边画成竖向 .在画两个相 交平面时,如果其中一个平面的一部分被另一个平面挡住,通 常把被挡住的部分画成 虚线 或不画.(如图③). ③

导 3.平面的表示法 ()用希腊字母α,β,等表示平面,例如:图①中的平面表示为 平面a (2)用代表平面的平行四边形的四个顶点的大写英文字母表 示平面,例如:图①中的平面表示为平面ABCD. (3)用代表平面的平行四边形相对的两个顶点的大写英文字 母表示平面,例如:图①中的平面表示为平面AC或平面BD
导航 3.平面的表示法 (1)用希腊字母α,β,γ等表示平面,例如:图①中的平面表示为 平面α. (2)用代表平面的平行四边形的四个顶点的大写英文字母表 示平面,例如:图①中的平面表示为平面ABCD. (3)用代表平面的平行四边形相对的两个顶点的大写英文字 母表示平面,例如:图①中的平面表示为平面AC或平面BD

导航 4.点、线、面之间的位置关系 位置关系 图形表示 符号表示 点与线 点A在直线a外 的位置 A a 关系 点B在直线a上 B 点与面 点A在平面a内 ●B 的位置 关系 点B在平面a外 ●A
导航 4 .点、线、面之间的位置关系 位置关系 图形表示 符号表示 点与线 的位置 关系 点 A 在直线 a 外 A ∉ a 点 B 在直线 a 上 B∈a 点与面 的位置 关系 点 A 在平面 α 内 A ∈ α 点 B 在平面 α 外 B∉α
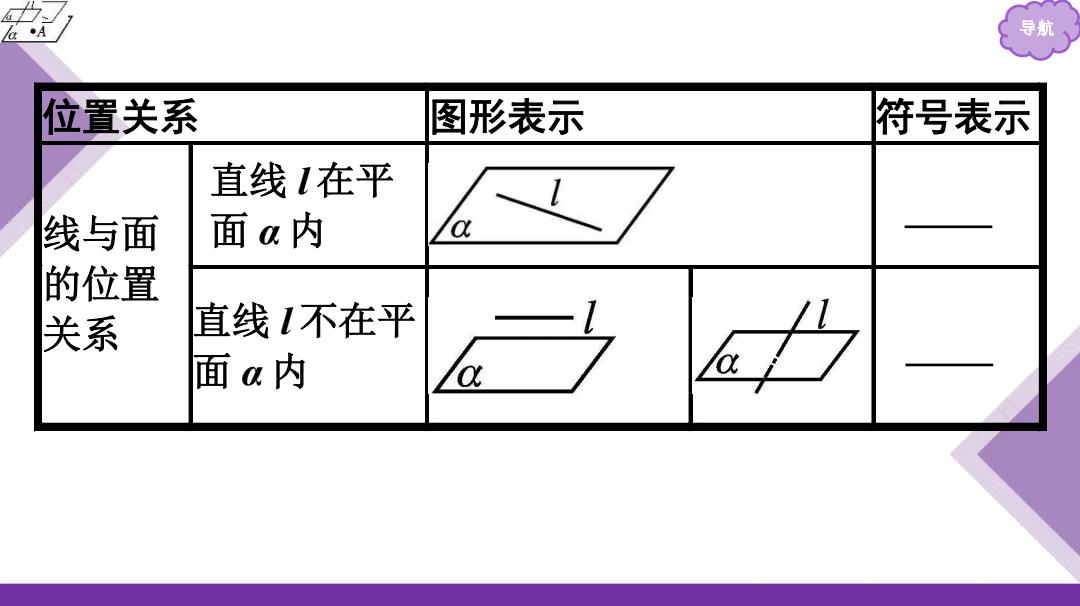
la A 导航 位置关系 图形表示 符号表示 直线1在平 线与面 面a内 a 的位置 关系 直线1不在平 面a内
导航 位置关系 图形表示 符号表示 线与面 的位置 关系 直线 l 在平 面 α 内 l⊂α 直线 l 不在平 面 α 内 l⊄α
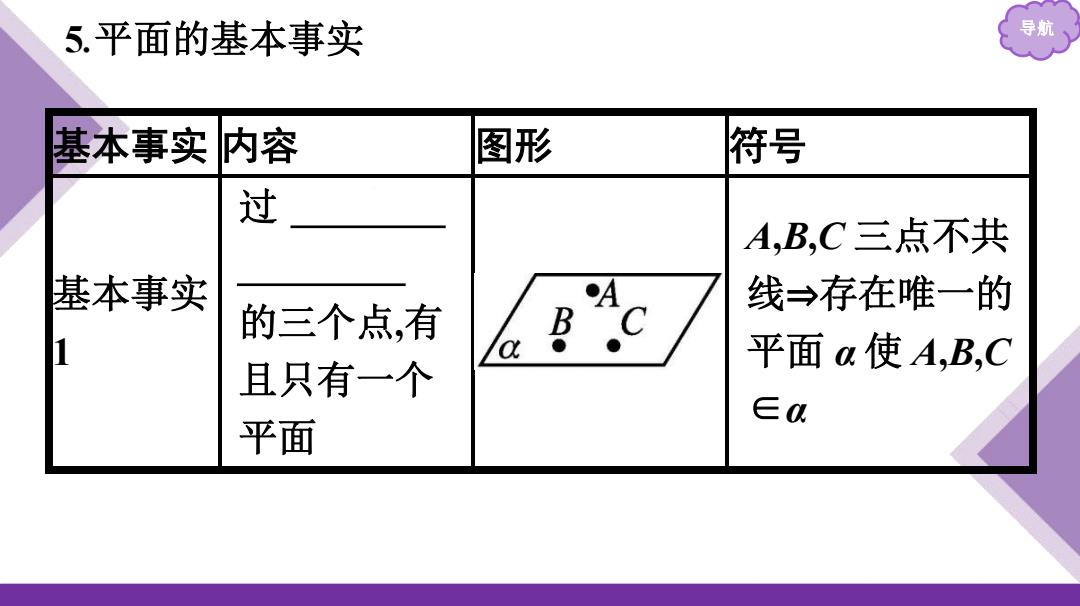
5.平面的基本事实 导航 基本事实内容 图形 符号 过 A,B,C三点不共 基本事实 A 线→存在唯一的 的三个点,有 B 平面a使A,B,C 且只有一个 ∈a 平面
导航 5 .平面的基本事实 基本事实 内容 图形 符号 基本事实 1 过 不在一 条直线上 的三个点,有 且只有一个 平面 A,B,C 三点不共 线⇒存在唯一的 平面 α 使 A,B,C ∈ α
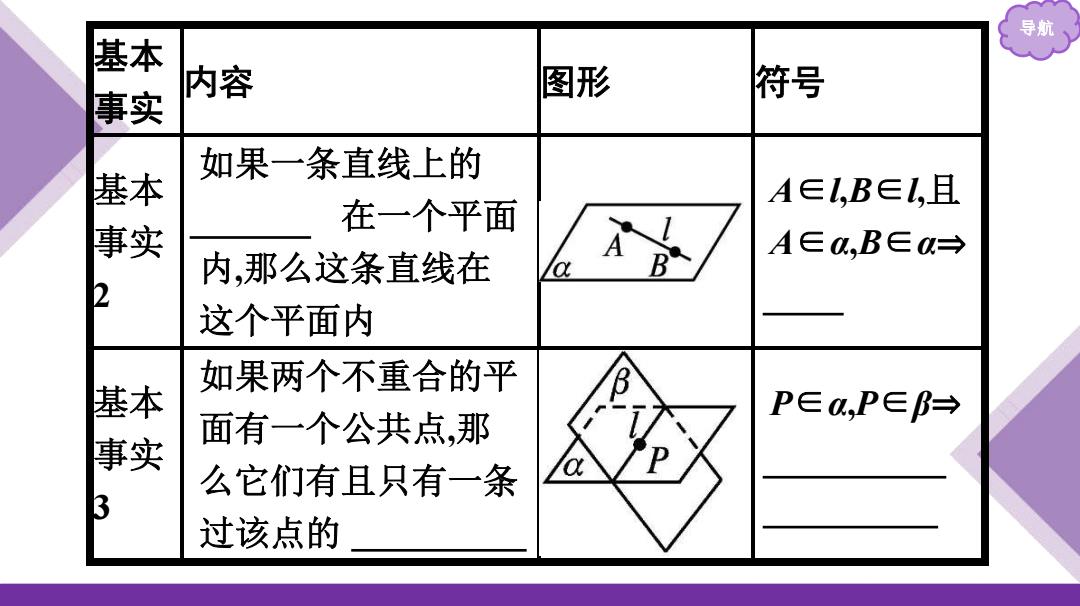
导航 基本 事实 内容 图形 符号 如果一条直线上的 基本 A∈L,B∈L,且 在一个平面 事实 A∈a,B∈a→ 内,那么这条直线在 B 2 这个平面内 如果两个不重合的平 基本 P∈a,P∈B→ 面有一个公共点,那 事实 么它们有且只有一条 3 过该点的
导航 基本 事实 内容 图形 符号 基本 事实 2 如果一条直线上的 两个点 在一个平面 内,那么这条直线在 这个平面内 A∈l,B∈l,且 A∈α,B∈α⇒ l⊂α 基本 事实 3 如果两个不重合的平 面有一个公共点,那 么它们有且只有一条 过该点的 公共直线 P∈α,P∈β⇒ α∩β=l 且 P ∈l

微思考2经过空间任意三点能确定一个平面吗? 提示:不一定,只有经过空间不共线的三点才能确定一个平 面. 6.基本事实的三个推论 推论1:经过一条直线和 ,有且只有一个 平面. 推论2:经过两条 直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面
导航 微思考2 经过空间任意三点能确定一个平面吗? 提示:不一定,只有经过空间不共线的三点才能确定一个平 面. 6.基本事实的三个推论 推论1:经过一条直线和 这条直线外一点 ,有且只有一个 平面. 推论2:经过两条 相交 直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面