
全程设计 第2课时 平面与平面垂直的性质定理
第2课时 平面与平面垂直的性质定理

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 平面与平面垂直的性质定理 文字 两个平面垂直,如果 有一直 语言 线垂直于这两个平面的 ,那么这条 直线与另一个平面
导航 课前·基础认知 平面与平面垂直的性质定理 文字 语言 两个平面垂直,如果 一个平面内 有一直 线垂直于这两个平面的 交线 ,那么这条 直线与另一个平面 垂直
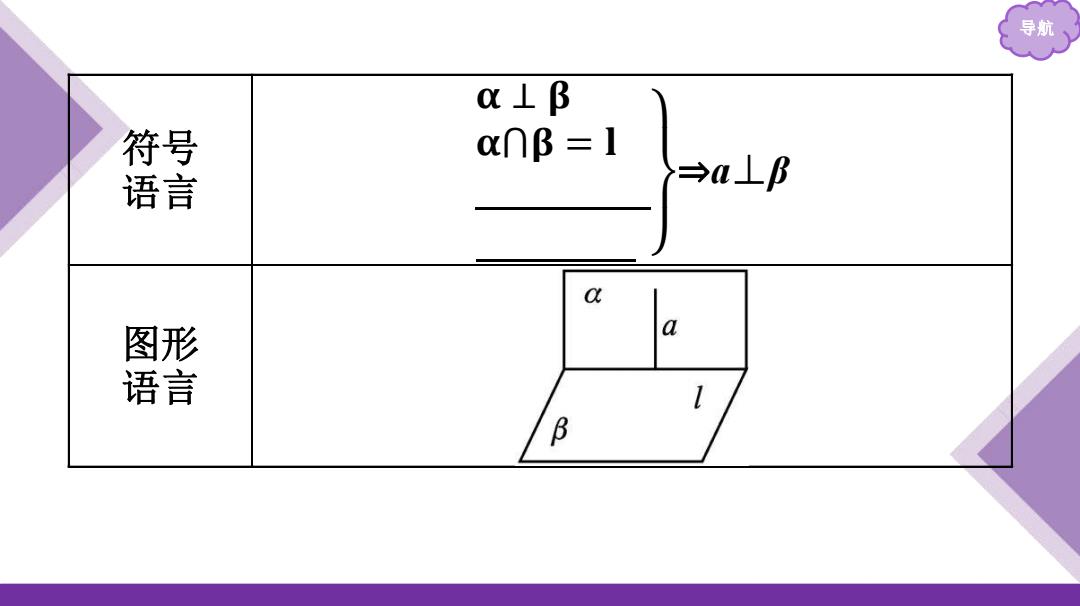
导航 o⊥β 冒 o∩B=1 →a⊥阝 a a 竖 β
导航 符号 语言 𝛂 ⊥ 𝛃 𝛂⋂𝛃 = 𝐥 𝐚 ⊂ 𝛂 𝐚 ⊥ 𝐥 ⇒a⊥β 图形 语言

导航 微思考若a⊥B,则a内的直线必垂直于内的无数条直线吗? 提示:正确.若设a∩B=l,aca,bcf,b⊥I,则a⊥b,故B内与b平行 的无数条直线均垂直于α内的任意直线 微拓展平面与平面垂直的性质定理揭示了面面垂直、线面 垂直及线线垂直间的内在联系,体现了数学中的化归、转化 思想,其转化关系如下: 线面垂直判定 面面垂直判定 线线垂直 线面垂直 面面垂直 线面垂直的 面面垂直的 定义是线线 性质是线面 垂直的判定 垂直的判定
导航 微思考 若α⊥β,则α内的直线必垂直于β内的无数条直线吗? 提示:正确.若设α∩β=l,a⊂α,b⊂β,b⊥l,则a⊥b,故β内与b平行 的无数条直线均垂直于α内的任意直线. 微拓展平面与平面垂直的性质定理揭示了面面垂直、线面 垂直及线线垂直间的内在联系,体现了数学中的化归、转化 思想,其转化关系如下:
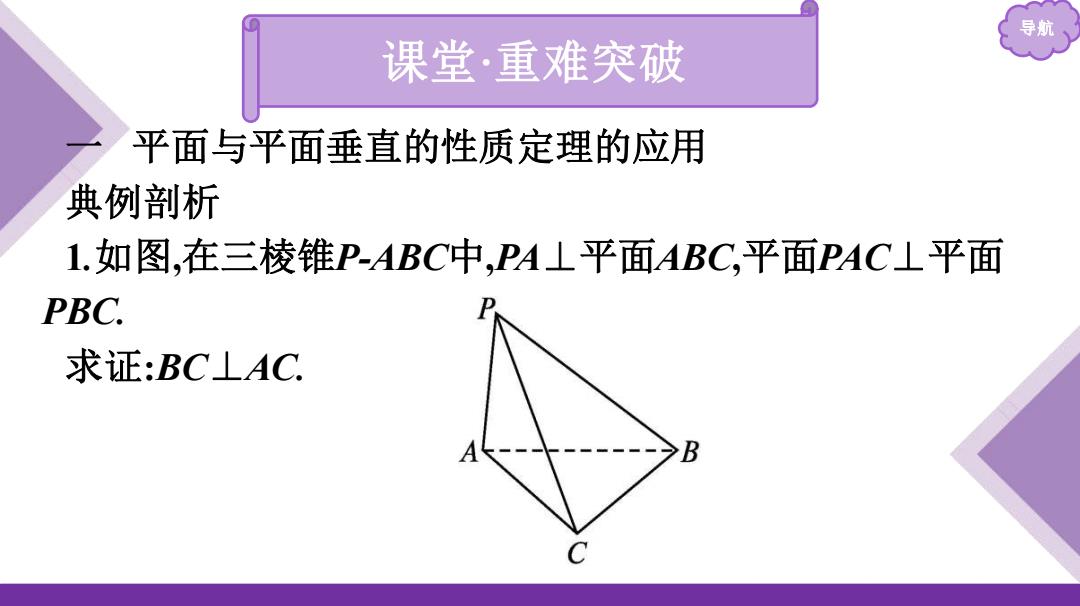
导航 课堂·重难突破 平面与平面垂直的性质定理的应用 典例剖析 1.如图,在三棱锥P-ABC中,PA⊥平面ABC,平面PAC⊥平面 PBC. 求证:BC⊥AC C
导航 课堂·重难突破 一 平面与平面垂直的性质定理的应用 典例剖析 1.如图,在三棱锥P-ABC中,PA⊥平面ABC,平面PAC⊥平面 PBC. 求证:BC⊥AC

导期 证明:如图,在平面PAC内作AD⊥PC于点D. .·平面PAC⊥平面PBC,ADc平面PAC,AD⊥PC,平面PAC∩ 平面PBC=PC,'.AD⊥平面PBC 又BCc平面PBC,'.AD⊥BC ,PA⊥平面ABC,BCC平面ABC, .PA⊥BC .AD∩PA=A,'.BC⊥平面PAC ,ACc平面PAC,..BC⊥AC
导航 证明:如图,在平面PAC内作AD⊥PC于点D. ∵平面PAC⊥平面PBC,AD⊂平面PAC,AD⊥PC,平面PAC∩ 平面PBC=PC,∴AD⊥平面PBC. 又BC⊂平面PBC,∴AD⊥BC. ∵PA⊥平面ABC,BC⊂平面ABC, ∴PA⊥BC. ∵AD∩PA=A,∴BC⊥平面PAC. ∵AC⊂平面PAC,∴BC⊥AC

导航 规律总结 1.证明或判定线面垂直的常用方法 ()直线与平面垂直的判定定理 (2)平面与平面垂直的性质定理, (3)若∥b,a⊥a,则b⊥a(a,b为直线,a为平面): (4)若a⊥a,a∥B,则a⊥(a为直线,a,P为平面). 2.利用两平面垂直的性质定理时,要将面面垂直转化为线面垂 直,方法是在其中一个面内作(找)与交线垂直的直线
导航 规律总结 1.证明或判定线面垂直的常用方法 (1)直线与平面垂直的判定定理. (2)平面与平面垂直的性质定理. (3)若a∥b,a⊥α,则b⊥α(a,b为直线,α为平面). (4)若a⊥α,α∥β,则a⊥β(a为直线,α,β为平面). 2.利用两平面垂直的性质定理时,要将面面垂直转化为线面垂 直,方法是在其中一个面内作(找)与交线垂直的直线
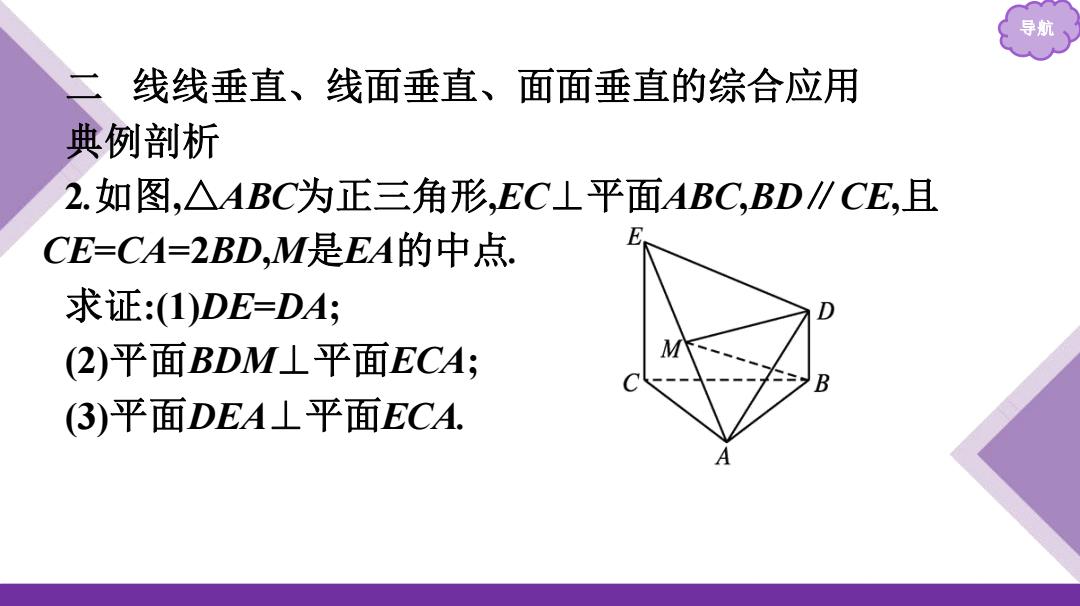
导航 二 线线垂直、线面垂直、面面垂直的综合应用 典例剖析 2.如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且 CE=CA=2BD,M是EA的中点. 求证:(1)DE=DA; (2)平面BDM⊥平面ECA; (3)平面DEA⊥平面ECA
导航 二 线线垂直、线面垂直、面面垂直的综合应用 典例剖析 2.如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且 CE=CA=2BD,M是EA的中点. 求证:(1)DE=DA; (2)平面BDM⊥平面ECA; (3)平面DEA⊥平面ECA

导 证明:(1)设BD=M,如图,作DF∥BC交CE于F,则CF=DB= 因为CE⊥平面ABC, 所以DE=VEF2+DFZ=V5a F 所以BC⊥CF,DF⊥EC, M 又因为DB⊥平面ABC, 所以DA=VDB2+AB2=V5a,所以DE=DA
导航 证明:(1)设BD=a,如图,作DF∥BC交CE于F,则CF=DB=a. 因为CE⊥平面ABC, 所以BC⊥CF,DF⊥EC, 又因为DB⊥平面ABC, 所以 DE= 𝑬𝑭𝟐 + 𝑫𝑭𝟐 = 𝟓a. 所以 DA= 𝑫𝑩𝟐 + 𝑨𝑩𝟐 = 𝟓a,所以 DE=DA