
全程设计 8.4.2 空间点、直线、 平面之间的 位置关系
8.4.2 空间点、直线、平面之间的 位置关系

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
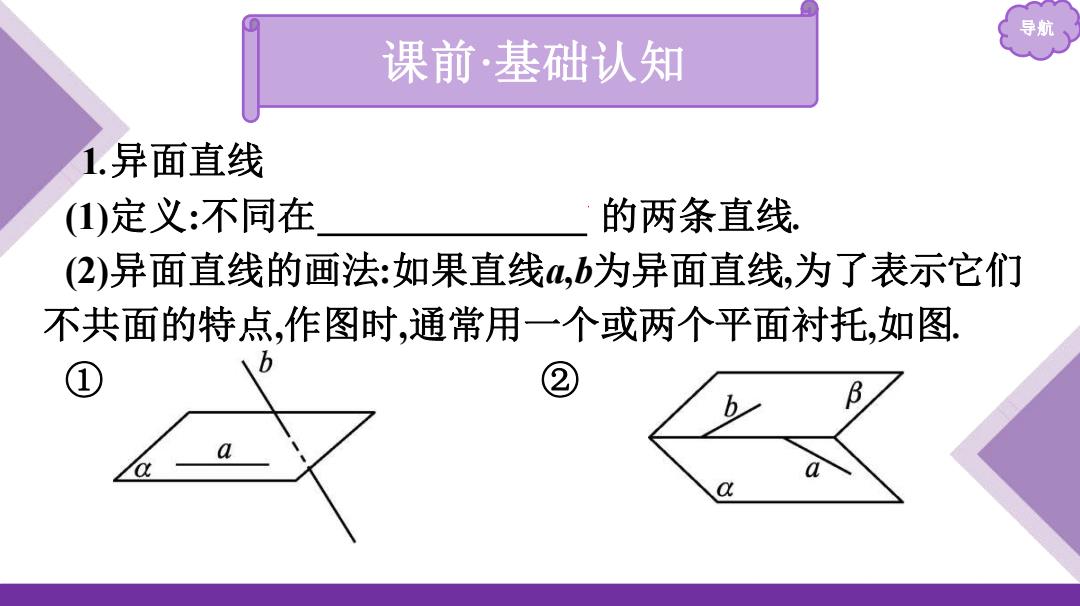
导航 课前·基础认知 1.异面直线 1)定义:不同在 的两条直线 (2)异面直线的画法:如果直线4,b为异面直线,为了表示它们 不共面的特点,作图时,通常用一个或两个平面衬托,如图! b
导航 课前·基础认知 1.异面直线 (1)定义:不同在 任何一个平面内的两条直线. (2)异面直线的画法:如果直线a,b为异面直线,为了表示它们 不共面的特点,作图时,通常用一个或两个平面衬托,如图. ① ②

导航 2.空间两条直线的位置关系 位置关系 特点 相交 在同一平面内,有且只有 公共点 平行 在同一平面内, 公共点 异面直线 不同在 内, 公共点 微思考1分别在两个平面内的两条直线一定是异面直线吗? 提示:不一定可能平行、相交或异面
导航 2.空间两条直线的位置关系 微思考1 分别在两个平面内的两条直线一定是异面直线吗? 提示:不一定.可能平行、相交或异面. 位置关系 特点 相交 在同一平面内,有且只有 一个 公共点 平行 在同一平面内, 没有 公共点 异面直线 不同在 任何一个平面 内, 没有 公共点
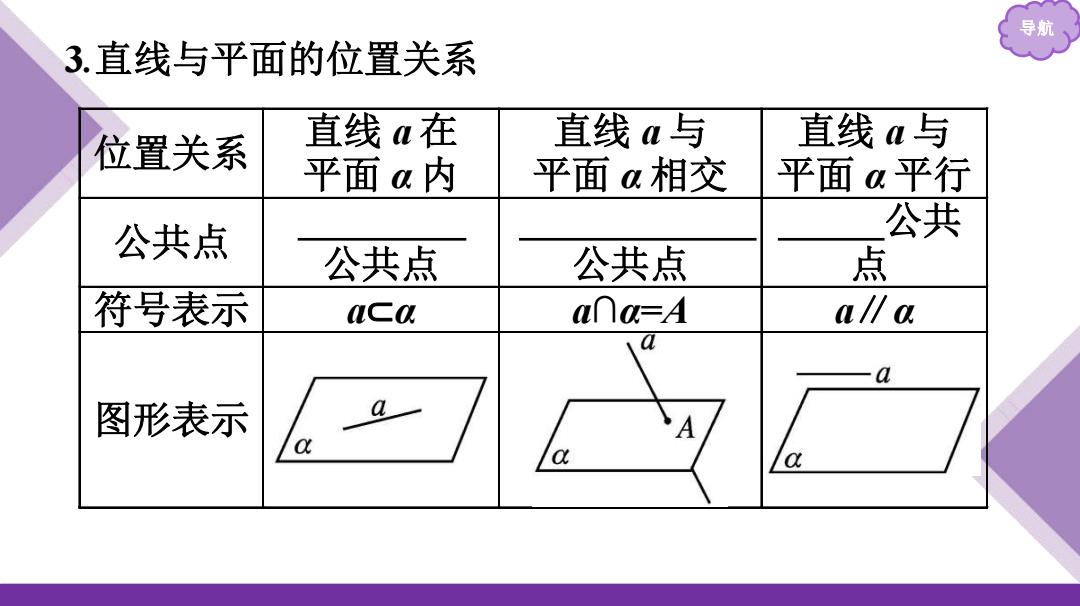
导航 3.直线与平面的位置关系 位置关系 直线a在 直线a与 直线a与 平面a内 平面a相交 平面a平行 公共点 公共 公共点 公共点 点 符号表示 aca a∩a=A a∥a -a 图形表示 a A a
导航 3 .直线与平面的位置关系 位置关系 直线 a 在 平面 α 内 直线 a 与 平面 α 相交 直线 a 与 平面 α 平行 公共点 有无数个 公共点 有且只有一个 公共点 没有 公共 点 符号表示 a ⊂ α a ∩ α =A a ∥ α 图形表示

导 微思考2“直线与平面不相交”与“直线与平面没有公共点” 是一回事吗? 提示:不是前者包括直线与平面平行及直线在平面内这 两种情况,而后者仅指直线与平面平行
导航 微思考2 “直线与平面不相交”与“直线与平面没有公共点” 是一回事吗? 提示:不是.前者包括直线与平面平行及直线在平面内这 两种情况,而后者仅指直线与平面平行
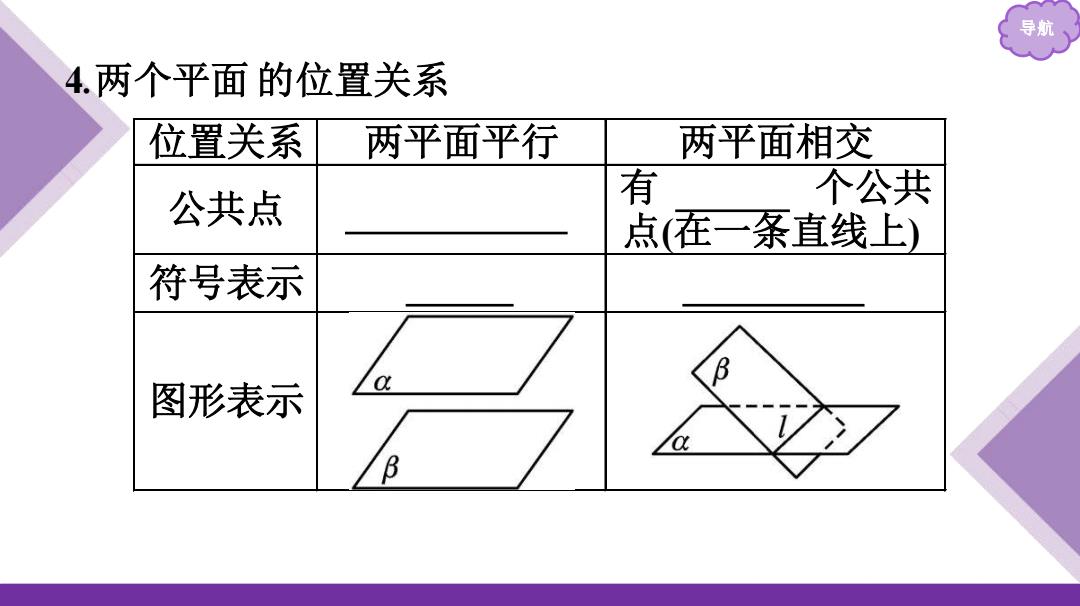
导航 4.两个平面的位置关系 位置关系 两平面平行 两平面相交 公共点 有 个公共 点(在一系直线上) 符号表示 B 图形表示 B
导航 位置关系 两平面平行 两平面相交 公共点 没有公共点 有 无数 个公共 点(在一条直线上) 符号表示 α ∥ β α ∩β=l 图形表示 4 .两个平面 的位置关系

导期 微探究 (1)若一个平面内的任意一条直线都与另一个平 面平行,那么这两个平面之间有什么位置关系? 提示:因为一个平面内任意一条直线都与另一个平面平 行,所以该平面与另一平面没有公共点,根据两平面平行的定 义知,这两个平面平行
导航 微探究 (1)若一个平面内的任意一条直线都与另一个平 面平行,那么这两个平面之间有什么位置关系? 提示:因为一个平面内任意一条直线都与另一个平面平 行,所以该平面与另一平面没有公共点,根据两平面平行的定 义知,这两个平面平行

导航 2)平面a内有无数条直线与平面平行,那么α∥B是否正确? 提示:不正确如图,设∩=l,则在平面a内可以有无数条与l 平行的直线41,42,,它们是一组平行线,这时a1,2,…都与平面 平行,但a不平行于B,而是a∩=l a a3 B
导航 (2)平面α内有无数条直线与平面β平行,那么α∥β是否正确? 提示:不正确.如图,设α∩β=l,则在平面α内可以有无数条与l 平行的直线a1 ,a2 ,…,它们是一组平行线,这时a1 ,a2 ,…都与平面 β平行,但α不平行于β,而是α∩β=l
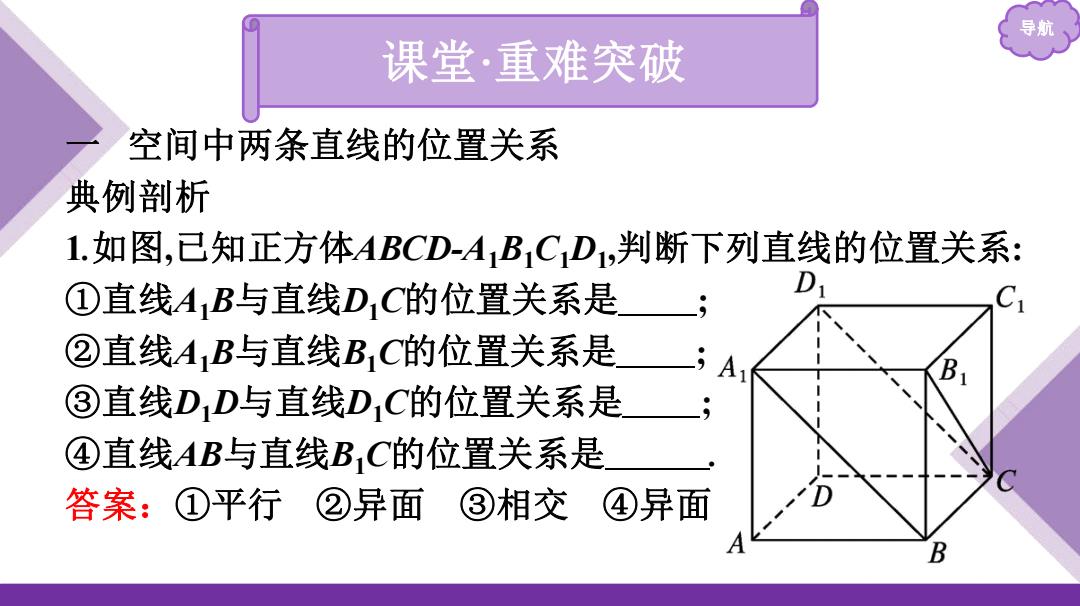
导航 课堂·重难突破 空间中两条直线的位置关系 典例剖析 1.如图,已知正方体ABCD-A1B1CD1,判断下列直线的位置关系: ①直线A,B与直线DC的位置关系是 D C ②直线A1B与直线BC的位置关系是 ③直线D1D与直线D,C的位置关系是 ④直线AB与直线B,C的位置关系是 答案:①平行②异面③相交 ④异面 B
导航 课堂·重难突破 一 空间中两条直线的位置关系 典例剖析 1.如图,已知正方体ABCD-A1B1C1D1 ,判断下列直线的位置关系: ①直线A1B与直线D1C的位置关系是 ; ②直线A1B与直线B1C的位置关系是 ; ③直线D1D与直线D1C的位置关系是 ; ④直线AB与直线B1C的位置关系是 . 答案:①平行 ②异面 ③相交 ④异面