
全程设计 第1课时 直线与平面垂直的判定定理
第1课时 直线与平面垂直的判定定理

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.直线与平面垂直的定义 如果直线l与平面a内的 定义 直线都垂直,我们就说直线l与平面α 互相垂直 记法 1⊥a 有关 直线1叫做平面a的 平面a叫 概念 做直线1的,它们唯一的公共点 P叫做
导航 课前·基础认知 1.直线与平面垂直的定义 定义 如果直线 l 与平面 α 内的 任意一条 直线都垂直,我们就说直线 l 与平面 α 互相垂直 记法 l⊥α 有关 概念 直线 l 叫做平面 α 的 垂线 ,平面 α 叫 做直线 l 的 垂面 ,它们唯一的公共点 P 叫做 垂足

导航 画法 画直线与平面垂直时,通常把直线画成 与表示平面的平行四边形的一边垂直 图示 性质 过一点垂直于已知平面的直线有且只有 一条 垂线 过一点作垂直于已知平面的直线,则该 段与 点与垂足间的线段,叫做这个点到该平 点面 面的垂线段,垂线段的长度叫做这个点 距 到该平面的距离
导航 画法 画直线与平面垂直时,通常把直线画成 与表示平面的平行四边形的一边垂直 图示 性质 过一点垂直于已知平面的直线有且只有 一条 垂线 段与 点面 距 过一点作垂直于已知平面的直线,则该 点与垂足间的线段,叫做这个点到该平 面的垂线段,垂线段的长度叫做这个点 到该平面的距离

导航 微思考1直线与平面垂直定义中的关键词“任意一条直线” 是否可以换成“所有直线“无数条直线”? 提示:定义中的“任意一条直线”与“所有直线”是等价的,但 是不能说成“无数条直线”,因为一条直线与某平面内无数条 平行直线垂直,该直线与这个平面不一定垂直
导航 微思考1 直线与平面垂直定义中的关键词“任意一条直线” 是否可以换成“所有直线”“无数条直线”? 提示:定义中的“任意一条直线”与“所有直线”是等价的,但 是不能说成“无数条直线”,因为一条直线与某平面内无数条 平行直线垂直,该直线与这个平面不一定垂直
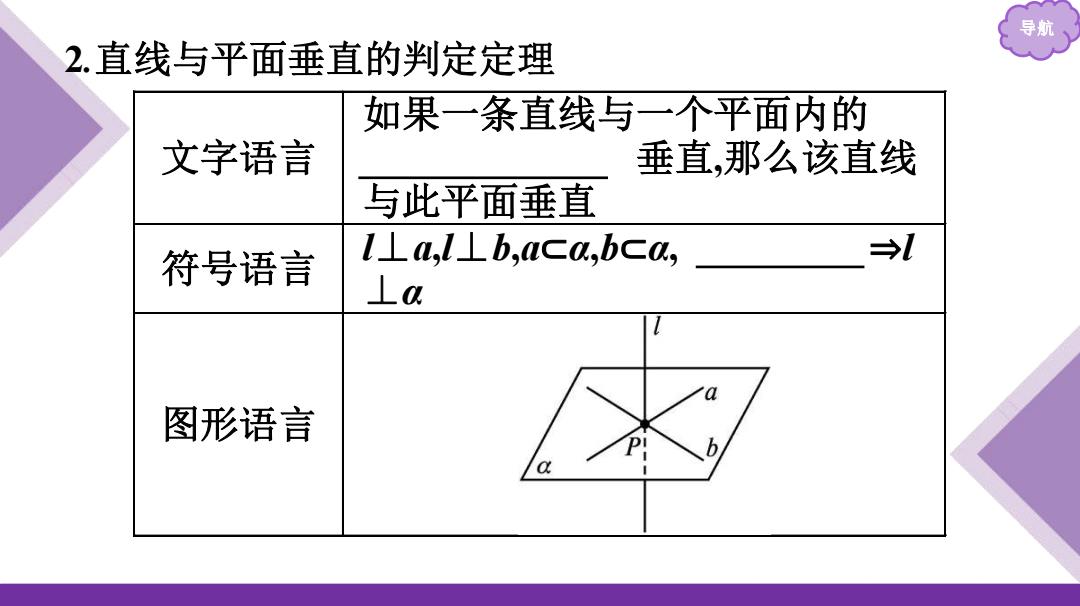
导航 2.直线与平面垂直的判定定理 如果一条直线与一个平面内的 文字语言 垂直,那么该直线 与此平面垂直 符号语言 l⊥a,l⊥b,aca,bca, →l ⊥a a 图形语言
导航 2 .直线与平面垂直的判定定理 文字语言 如果一条直线与一个平面内的 两条相交直线 垂直,那么该直线 与此平面垂直 符号语言 l⊥ a,l⊥ b,a ⊂ α,b ⊂ α, a ∩ b =P ⇒l ⊥α 图形语言
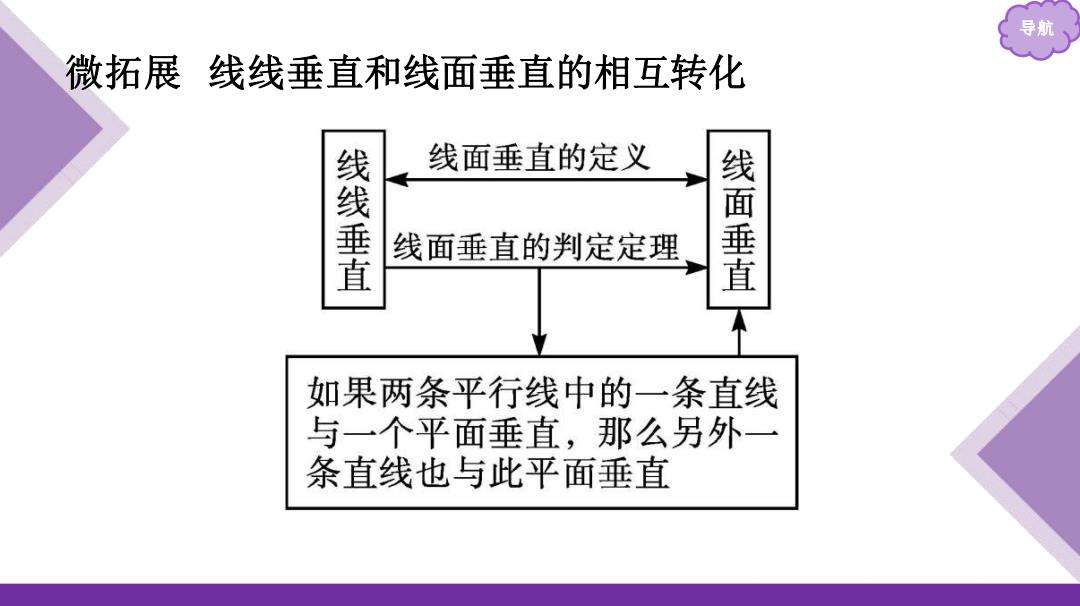
导航 微拓展线线垂直和线面垂直的相互转化 线面垂直的定义 线线垂直 线面垂直的判定定理 线面垂直 如果两条平行线中的一条直线 与一个平面垂直,那么另外一 条直线也与此平面垂直
导航 微拓展 线线垂直和线面垂直的相互转化

导航 3.直线和平面所成的角 有关概念 对应图形 斜 一条直线1与一个平面 ,但不 与这个平面a,如图中直线PA 足 斜线和平面的 ,如图中点A 过斜线上斜足以外的一点P向平面a 引 PO,过 O和A的 影 直线AO叫做斜线在这个平面上的射 影
导航 3 .直线和平面所成的 角 有关概念 对应图形 斜线 一条直线 l 与一个平面 α 相交 ,但不 与这个平面 α 垂直 ,如图中直线 PA 斜足 斜线和平面的 交点 ,如图中点 A 射影 过斜线上斜足以外的一点 P 向平面 α 引 垂线 PO,过 垂足 O 和 斜足 A 的 直线 AO 叫做斜线在这个平面上的射 影

导航 有关概念 对应图形 定义:平面的一条斜线和它在平 直线和 面上的射影所成的角 平面所 规定:一条直线垂直于平面,它 成的角 们所成的角是 ;一条直 线和平面平行或在平面内,它们 所成的角是 取值 范围
导航 有关概念 对应图形 直线和 平面所 成的角 定义:平面的一条斜线和它在平 面上的射影所成的角 规定:一条直线垂直于平面,它 们所成的角是 90° ;一条直 线和平面平行或在平面内,它们 所成的角是 0° 取值 范围 𝟎, 𝝅 𝟐

微思考2(1)若图中的∠POA是斜线PO与平面a所成的角 则需具备哪些条件? 提示:需要PA⊥a,A为垂足,OA为斜线PO的射影,这样 ∠POA就是斜线PO与平面a所成的角. (2)空间几何体中,如何确定直线与 平面所成的角? 提示:过斜线上一点向平面作垂线, 确定垂足位置,则射影确定,直线与平 面所成的角也确定
导航 微思考2 (1)若图中的∠POA是斜线PO与平面α所成的角, 则需具备哪些条件? 提示:需要PA⊥α,A为垂足,OA为斜线PO的射影,这样 ∠POA就是斜线PO与平面α所成的角. (2)空间几何体中,如何确定直线与 平面所成的角? 提示:过斜线上一点向平面作垂线, 确定垂足位置,则射影确定,直线与平 面所成的角也确定