
试卷代号:1009 座位■口 中央广播电视大学2011一2012学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本)试题 2012年1月 题 号 二 三 四 五 六 总分 分 数 得 分 评卷人 一、单项选择题(每小题3分,本题共15分) 1.若集合A的元素个数为10,则其幂集的元素个数为(). A.10 B.100 C.1024 D.1 2.设A={a,b},B={1,2},R1,R2,R3是A到B的二元关系,且R={,}, R2={,,),R=(,},则( )是从A到B的函数 A.R1和R2 B.R2 C.R, D.R,和R 3.设A={1,2,3,4,5,6,7,8},R是A上的整除关系,B一{2,4,6},则集合B的最大元、 最小元、上界、下界依次为(). A.8、2、8、2 B.无、2、无、2 C.6、2、6、2 D.8、1、6、1 4.若完全图G中有n个结点(n≥2),m条边,则当( )时,图G中存在欧拉回路, A.n为奇数 B.n为偶数 C.m为奇数 D.m为偶数 67
试卷代号 9座位号 中央广播电视大学 11 2学年度第一学期"开放本科"期末考试(半开卷) 离散数学(本)试题 2012 年1 |题号|一|二|三 l四|五|六|总分| |分数 I I I I I I I 题{每小题 3分,本题共 5分) I I I 1.若集合 A的元素个数为 0,则其幕集的元素个数为( A.10 B. 100 C. 1024 D. 1 2. {1 ,2} 且R ={,} , Rz= { , ,} 凡={ ,} )是从 A.R 和R C. R3 B.Rz D.R 和R 3. R是 A上的整除关系 {2 ,4 ,6} 合B 最小元、上界、下界依次为( ). A.8 、2 ,8 、2 C. U8 、1 、6 、1 4. 图G 个结 三~2) )时,图 G中存在欧拉回路. A.n C.m 为奇数D.m 偶数 67

5.已知图G的邻接矩阵为 (0001 1) 0 0001 0 0011 1 0101 1 1110 则G有(). A.6点,8边 B.6点,6边 C.5点,8边 D.5点,6边 得 分 评卷人 二、填空题(每小题3分,本题共15分) 6.设集合A={a},那么集合A的幂集是 7.若R:和R2是A上的对称关系,则R1UR,R1∩R2,R1一R2,R2一R,中对称关系有 个 8.设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去 条边后 使之变成树. 9.设连通平面图G的结点数为5,边数为6,则面数为 10.设个体域D={a,b},则谓词公式(Vx)(A(x)∧B(x))消去量词后的等值式为 得分 评卷人 三、逻辑公式翻译(每小题6分,本题共12分) 11.将语句“今天有联欢活动,明天有文艺晚会.”翻译成命题公式. 12.将语句“如果小王来,则小李去.”翻译成命题公式. 68
5. 图G 邻接矩阵为 00011 o 000 1 00011 1 0 1 0 1 1 1 1 1 0 ). A.6 ,8 C.5 ,8 |得分|评卷人| I I I B.6 ,6 D.5 ,6 二、填空题(每小题 3分,本题共 5分} 6. 集合 合A 事集 7. 是A 对称关 则R URz ,Rl n 对称 个. 8. 图G 有5 点度 总和为10 从G 删去 使之变成树. 9. 连通平 图G 为5 为6 则 面 10. 设个体域D= {a 则 谓 词 Vx) (A (x) (x)) 去 量 词 后 得分|评卷人 三、逻辑公式翻译(每小题6分,本题共 2分) 1. 将语 联欢 天有 艺 晚 题公 12. 小李 68

得分 评卷人 四、判断说明题(每小题7分,本题共14分) 判断下列各题正误,并说明理由· 13.若偏序集的哈斯图如图一所示,则集合A的最大元为a,极小元不存在. a 图一 14.P∧(P+Q)VP为永假式. 分 评卷人 五、计算题(每小题12分,本题共36分)】 15.设集合A=(1,2,3,4},R={|x,y∈A;x-yl=1或x-y=0),试 (1)写出R的有序对表示; (2)画出R的关系图; (3)说明R满足自反性,不满足传递性, 16.设图G=,V={1,2,,v4,5},E={(1,2),(U1,3),(v2,4),(3,5), (4,5)},试 (1)画出G的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出图G的补图的图形 17.求P→Q∧R的合取范式与主析取范式. 得 分 评卷人 六、证明题(本题共8分) 18.设连通无向图G有14条边,3个4度顶点,4个3度顶点,其它顶点的度数均小于3, 试说明G中可能有的顶点数. 69
|得分|评卷人| I I I 四、判断说明题{每小题 7分,本题共 14分) 判断下列各题正误,并说明理由. 13. 偏序集 一所 合A 大元 极小元 存在 /气 14. -, P A (P -,Q)VP 永假 |得分|评卷人| I I I 五、计算题{每小题 2分,本题共 6分} 15. 合A= {l ,2 ,3 yεA =1 或x-y=O} (1)写出 R的有序对表示; (2) 出R (3) 明R 满足 不满足传 16. 't } , E = {(VI' Vz ) , (VI' V3 ) , (吨 (叫, , (叭, ,试 (1)画出 G的图形表示 (2) 邻接 (3) (4) 图G 17. 求P 八R 合取 析取范 |得分|评卷人| I I I 六、证明题{本题共 8分) 18. 通无 图G 有14 ,3 个4 ,4 个3 于3 试说明 G中可能有的顶点数. 69

试卷代号:1009 中央广播电视大学2011一2012学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本)试题答案及评分标准 (供参考) 2012年1月 一、单项选择题(每小题3分,本题共15分】 1.C 2.C 3.B 4.A 5.D 二、填空题(每小题3分,本题共15分)】 6.{,{a} 7.4 8.1 9.3 10.(A(a)AB(6))∧(A(a)B(b) 三、逻辑公式翻译(每小题6分,本题共12分) 11.设P:今天有联欢活动,Q:明天有文艺晚会, (2分) P∧Q. (6分) 12.设P:小王来,Q:小李去 (2分) P→Q (6分) 四、判断说明题(每小题7分,本题共14分)】 13.错误. (3分) 对于集合A的任意元素x,均有∈R(或xRa),所以a是集合A中的最大元.(5分) 但按照极小元的定义,在集合A中b,c,d均是极小元. (7分) 14.错误, (3分) PA(P→nQ)VP是由PA(P+Q)与P组成的析取式, 如果P的值为真,则PA(P一Q)VP为真, (5分) 如果P的值为假,则P与P+Q为真,即P∧(P·Q)为真, 70
试卷代号 0 0 中央广播电视大学 2 0 11 2 0 2学年度第一学期"开放本科"期末考试(半开卷) 离散数学(本)试题答案及评分标准 (供参考〉 2012 年1 -、单项选择题{每小题 3分,本题共 5分} I. C 2.C 3. B 4.A 5.0 二、填空题{每小题3分.本题共 5分} 6. {正当 {a}} 7.4 8.1 9.3 10. (A(a) 八B(b» 八(A(a) 八B(b» 三、逻辑公式翻译{每小题 6分,本题共 2分} 1. 天有联欢 12. 小李 P• Q. (2 (6 (2 (6 四、判断说明题{每小题 7分,本题共 14分} 13. (3 对于集合 A的任意元素工,均有 ε R ,所以 a是集合 A中的最大元. (5 但按照极小元的定义,在集合 A中 d均是极小元. (7 14. (3 ""PA (P•""Q) V 由""PA (P "" 与P 如果 为真 ..., "" (5 如果 ..., "" ..., "" 70
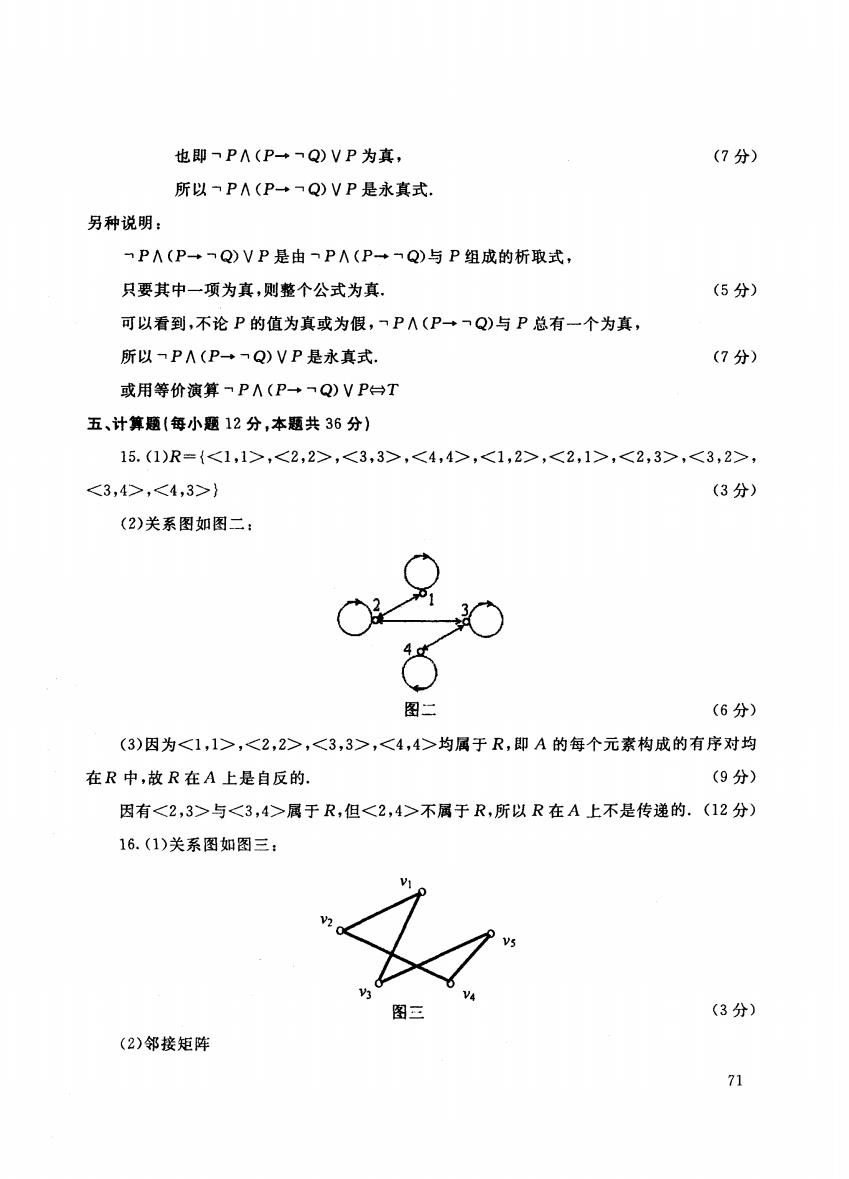
也即PA(PQ)VP为真, (7分) 所以一PA(P+Q)VP是永真式 另种说明: 一P∧(P+Q)VP是由一P∧(P+一Q)与P组成的析取式, 只要其中一项为真,则整个公式为真, (5分) 可以看到,不论P的值为真或为假,一P∧(P→一Q)与P总有一个为真, 所以P∧(P→Q)VP是永真式, (7分) 或用等价演算P∧(P+Q)VP台T 五、计算题(每小题12分,本题共36分) 15.(1)R={,,,,,,,, ,} (3分) (2)关系图如图二: 图二 (6分) (3)因为,,,均属于R,即A的每个元素构成的有序对均 在R中,故R在A上是自反的. (9分) 因有与属于R,但不属于R,所以R在A上不是传递的.(12分) 16.(1)关系图如图三: 图三 (3分】 (2)邻接矩阵 71
也即 "" "" P为真. (7 所以 "" (P• ""Q) V 是永 另种说明 ""PA(P→""Q)VP 由""PA(P→""Q) 取式 只要其中一项为真,则整个公式为真. (5 可以看到,不论 P的值为真或为假 ""PA (P→""Q) 总有一 所以 ..., "" P是永真式. (7 或用等价演算"" "" 五、计算题{每小题 2分,本题共 6分) 15. (l)R = {. ..... .. .} (2) 系 图 (3 图二二 (3) 为... 即A 构成 R中,故 R在 A上是自反的. (9 因有 >与 3, >属于 ,但 >不属于 .所以 R在A上不是传递的. (1 2分) 16. (1)关系图如图三 V2 (2) 图三 V4 Vs (3 71

[01100] 1001 0 10001 (6分) 01001 00110 (3)deg(o1)=2 deg(v2)=2 deg(v3)=2 deg(va)=2 (9分) deg(vs)=2 (4)补图如图四 图四 (12分) 17.P→(R∧Q) 台PV(RAQ) (4分) 台(PVQ)∧(PVR) (合取范式) (6分) P+(R∧Q) 台PV(R∧Q) 台(PA(QVQ)V(RAQ) (7分) 曰(P∧Q)V(P∧Q)V(RAQ) (8分) 曰(P∧Q)A(RVR))V(PAQ)V(RAQ) (9分) 台(PAQ∧R)V(PAQ∧R)V(PAQ)V(RAQ) (10分) =(PA-QA-R)V(-PA-QAR)V(PAQ)∧(RVR))V(R∧Q) 台(P∧QAR)V(PQAR)V(PAQA-R)V(P∧Q∧R)V(RAQ) 台(PA-QA-R)V(PA-QAR)V(P∧Q∧R)V 72
O 1 1 O O 1 O O 1 O 1 O O O 1 (6 O 1 O O 1 LO O 1 1 O (3) deg ( VI ) = 2 deg(V2) =2 deg(叫)=2 deg(叫)=2 (9 deg(V5)=2 (4) V2 主二 图四 (1 2 (4 (6 (7 估分〉 (9 (1 (合取范式) 件(--, --, V(--, V(R 1\Q) 件« --, P 1\ --, Q) 1\ (--, RVR» V( --, 八Q)V(R 八Q) 件( --, p八--, Q八 --, V(--, --,Q 八R) V (--, 件( --, p八 --, I\ --, (--, PI\--, Q八 V« --, 八Q) 1\ ( --, R VR» V (R 八Q) 件( --, P 1\ --, Q1\ --, R) V( --, P 1\ --, Q1\R) V( --, P 1\Q1\ --, R) V( --, P 1\ 八R) V(R AQ) 17. →(R 件--, R八 件(--, PV Q) --, PV R) →(R 件--, R八 件( --, P 1\ ( --, Q VQ» V (R --' --, Q八 --, V(--, --, Q1\R) V( --, P 1\ --, V 72

(-PAQAR)V((-PVP)A(RAQ)) (P∧QAR)V(P∧QAR)V(PAQ∧R)V (-PAQAR)V(PARAQ) (主析取范式) (12分) 说明:此题解法步骤多样,若能按正确步骤求得结果,均可给分 六、证明题(本题共8分) 18.证明:可利用数列可图化及握手定理解答 顶点度数和为2×14=28, (2分) 28一(3×4+4×3)=4,则知其他顶点度数和为4, (4分) 对于有限图,若无零度顶点,则除4度及3度顶点外,可能的顶点情况有: 2个2度点; 1个2度点和2个1度点; 4个1度点; (6分) 即对应图的顶点数分别至少为9、10、11. (8分) 73
(-, V (( -, P V P) 1\ (R 件( -, P 1\ -, Q 1\ -, R) V ( -, P 1\ -, V ( -, I\ -, R ) V (-'P I\ 八R)V(P 八R 1\Q) (主析取范式) (12 说明 此题解法步骤多样,若能按正确步骤求得结果,均可给分. 六、证明题(本题共8分} 18. 化及 解答 顶点度数和为 8, (2 28 一(3X4+4X3)=4 其他 为4 (4 对于有限图,若无零度顶点,则除4度及 3度顶点外,可能的顶点情况有: 个2 个2 和2 个1 度点 个1 (6 即对应图的顶点数分别至少为9、 0、 1 1. (8 73