
试卷代号:1009 座位号■■ 中央广播电视大学2012一2013学年度第二学期“开放本科”期末考试(半开卷) 离散数学(本)试题 2013年7月 题 号 二 三 四 五 六 总分 分 数 得 分 评卷人 一、单项选择题(每小题3分,本题共15分】 1.若集合A={a,b},则下列表述正确的是(). A.0∈A B.{a}∈A C.{a,b}∈A D.{a}∈A 2.设A={1,2,3,4,5,6},B={1,2,3},A到B的关系R={(x,y〉|x∈A,y∈B,x=y2}, 则R=(). A.{,} B.{,) C.{,} D.{,} 3.n阶无向完全图K.的边数及每个结点的度数分别是( ) A.n(n-1)/2,n-1 B.n-1:n C.n(n-1),n-1 D.n(n-1),n 4.设无向完全图K.有n个结点(n≥2),m条边,当( )时,K中存在欧拉回路 A.m为奇数 B.n为偶数 C.n为奇数 D.m为偶数 5.设个体域为整数集,则公式Vx3y(x十y=0)的解释可为(). A.存在一整数x有整数y满足x十y=0 B.对任一整数x存在整数y满足x十y=0 C.存在一整数x对任意整数y满足x十y=0 D.任一整数x对任意整数y满足x十y=0 61
试卷代号 0 0 座位号 中央广播电视大学 3学年度第二学期"开放本科"期末考试(半开卷) 离散数学(本)试题 2013 年7 |题号|一|二|三|四|五|六|总分| |分数 I / I I I I I |得分|评卷人| 一、单项选择题{每小题 3分,本题共 5分} I I I 1.若集合 ,的,则下列表述正确的是( ). A. 0εA B. {a}EA C. {a ,b} D. {a}CA 2. {I , 2, 3, 4, 5, 6}, B = {1, 2 , 3} A到 B的关系 y勺, ). A. { , } B. { , } C. {, } D. {,} 3.n 边数及每个 数分 ). A. n(n-l)/2 ,n-l c. n(n-l) ,n - l B. n-l ,n D. n(n-l) ,n 4. 设元 )时 .中存在欧拉回路. A.m 数B.n c. 偶数 5. 体域 数集 "I 丑 y 释可 ). A. 在一整数 满足 B.对任一整数Z存在整数y满足 c.存在一整数z对任意整数y满足 D. 任意 满足 61

得分 评卷人 二、填空题(每小题3分,本题共15分) 6.设集合A={1,2,3,4},B={3,4,5,6},C={5,6,7,8},则A∩BUC等 于 7.设A={a,b},B={1,2},C={4,5},从A到B的函数f={,},从B到 C的函数g={,),则gf等于 8.设G是一个图,结点集合为V,边集合为E,则G的结点度数之和 为」 9.设G是具有n个结点m条边k个面的连通平面图,则n十k一m等于 10.设个体域D={1,2,3,4},A(x)为“x等于3”,则谓词公式(3x)A(x)的真值 为 得 分 评卷人 三、逻辑公式翻译(每小题6分,本题共12分)】 11.将语句“他们明天去旅游,仅当明天天晴.”翻译成命题公式. 12.将语句“小王是个学生,小李是个职员,而小张是个军人.”翻译成命题公式 得分 评卷人 四、判断说明题(每小题7分,本题共14分) 判断下列各题正误,并说明理由. 13.设A={1,2,3},R={,,,},则R是等价关系. 14.谓词公式(3x)P(x,y)→(H)Q(x,y,x)中3x量词的辖域为P(x,y)→(Vz)Q(x, y,z). 62
得分 i评卷人 二、填空题{每小题 3分,本题共 5分} 6. 合A = {l, 2, 3, 4} , B = {3 , 4, 5, 6} , C= {5 , 6, 7, 8} 则AnBUC 7. ,B = {I, 2},C = {4 从A 到B { ,} of 8. 设G 结 点 集 合 为E 则G 结 点 9. 设G 边h - m 10. 设个 域D= {1 ,2 ,3 ,4} 则 谓 得分|评卷人 三、逻辑公式翻译{每小题 6分,本题共 2分) 1. 将语 天去 当 明 天天 题公式 12. 小李 个职 军人 命题 |得分|评卷人| I I I 四、判断说明题(每小题 7分,本题共 4分) 判断下列各题正误,并说明理由. 13. A = {I , 2, 3},R = { , ,, 2, },则 R是等价关系. 14. 谓词公式 z)Q(x ,z) 中3x (x , y )• ( Vz)Q(x , y ,z ) . 62
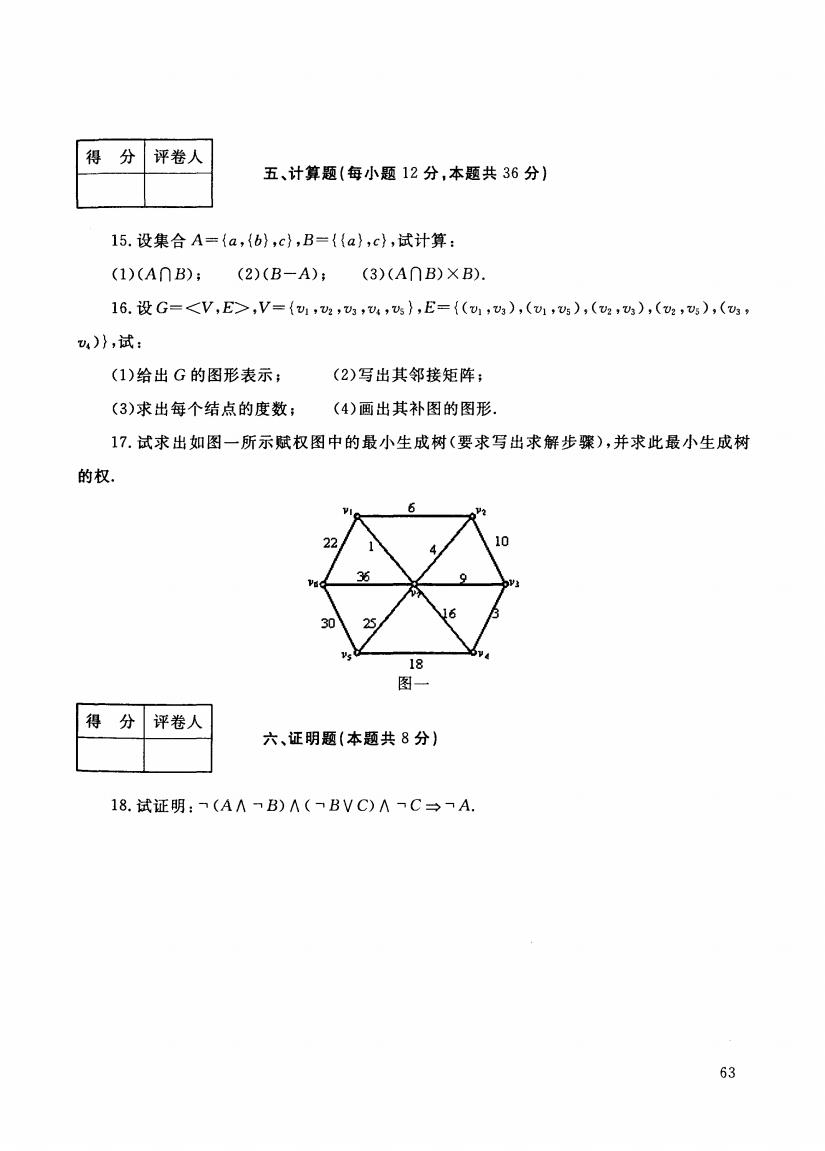
得分 评卷人 五、计算题(每小题12分,本题共36分) 15.设集合A={a,{b},c},B={a},c},试计算: (1)(A∩B); (2)(B-A): (3)(A∩B)XB) 16.设G=,V={U1,2,3,4,},E={(1,3),(1,05),(2,),(2,5),(3, v4)},试: (1)给出G的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出其补图的图形. 17.试求出如图一所示赋权图中的最小生成树(要求写出求解步骤),并求此最小生成树 的权 6 30 25 18 图 得 分 评卷人 六、证明题(本题共8分)】 18.试证明:(A∧B)A(BVC)∧C→A. 63
|得分|评卷人| I I I 五、计算题(每小题 2分,本题共 6分} 15. (1 )(A n B ) ; (2)(B-A); (3)(A门B) XB). 16. j ' 叫, V5 } ,E = {(VI , V 3 ) , (VI' V5 ) , ( V2 , V 3 ) , ( V2 , V 5 ) , ( V3 , 叫) } ,试 (1)给出 G的图形表示; (2) 其邻接 (3) (4) 图 的 17. 一所 小生成树 ,并求此最小生成树 的权. l'd 18 图一 ,1'j |得分|评卷人| Ll I 六、证明题(本题共 8分) 18. --, (A I\ --, --, B V C) 1\ --, C =字 --' 63

试卷代号:1009 中央广播电视大学2012一2013学年度第二学期“开放本科”期末考试(半开卷) 离散数学(本)试题答案及评分标准 (供参考) 2013年7月 一、单项选择题(每小题3分,本题共15分)】 1.D 2.B 3.A 4.C 5.B 二、填空题(每小题3分,本题共15分) 6.{3,4,5,6,7,8} 7.{,} 8.2!E1(或“边数的两倍”) 9.2 10.真(或T,或1) 三、逻辑公式翻译(每小题6分,本题共12分)】 11.设P:他们明天去旅游,Q:明天天晴. (2分)》 则命题公式为:PQ (6分) 12.设P:小王是个学生,Q:小李是个职员,R:小张是个军人. (2分) 则命题公式为:P∧Q∧R (6分) 四、判断说明题(每小题7分,本题共14分)】 13.错误。 (3分) R不是等价关系,因R中不包含,故不满足自反性. (7分) 14.错误 (3分) 因为紧接于量词之后最小的子公式称为量词的辖域, 所以3x量词的辖域为P(x,y). (7分)》 五、计算题(每小题12分,本题共36分) 15.(1)(A∩B)={c}: (4分) 64
试卷代号 中央广播电视大学 3学年度第二学期"开放本科"期末考试(半开卷) 离散数学(本)试题答案及评分标准 (供参考) 2013 年7 一、单项选择题(每小题 3分,本题共 5分} l. D 2.B 3.A 4.C 5. B 二、填空题(每小题 3分,本题共 5分) 6. {3,4 ,5 ,6 ,7 ,8} 7. { ,} 8. 21EI (或"边数的两倍") 9.2 10. 1) 三、逻辑公式翻译(每小题6分,本题共 2分} 1. 天去旅游 天 晴 则命题公式为 • Q . 12. 是个学生 李是个职 则命题公式为 四、判断说明题(每小题 7分,本题共 4分) 13. 错误 因R 含 故不 14. 因为紧接于量词之后最小的子公式称为量词的辖域, 所以 量词 辖域 五、计算题(每小题 2分,本题共 6分) 15. (l )(A n B> = {c}; 64 (2 (6 (2 (6 (3 (7 (3 (7 (4
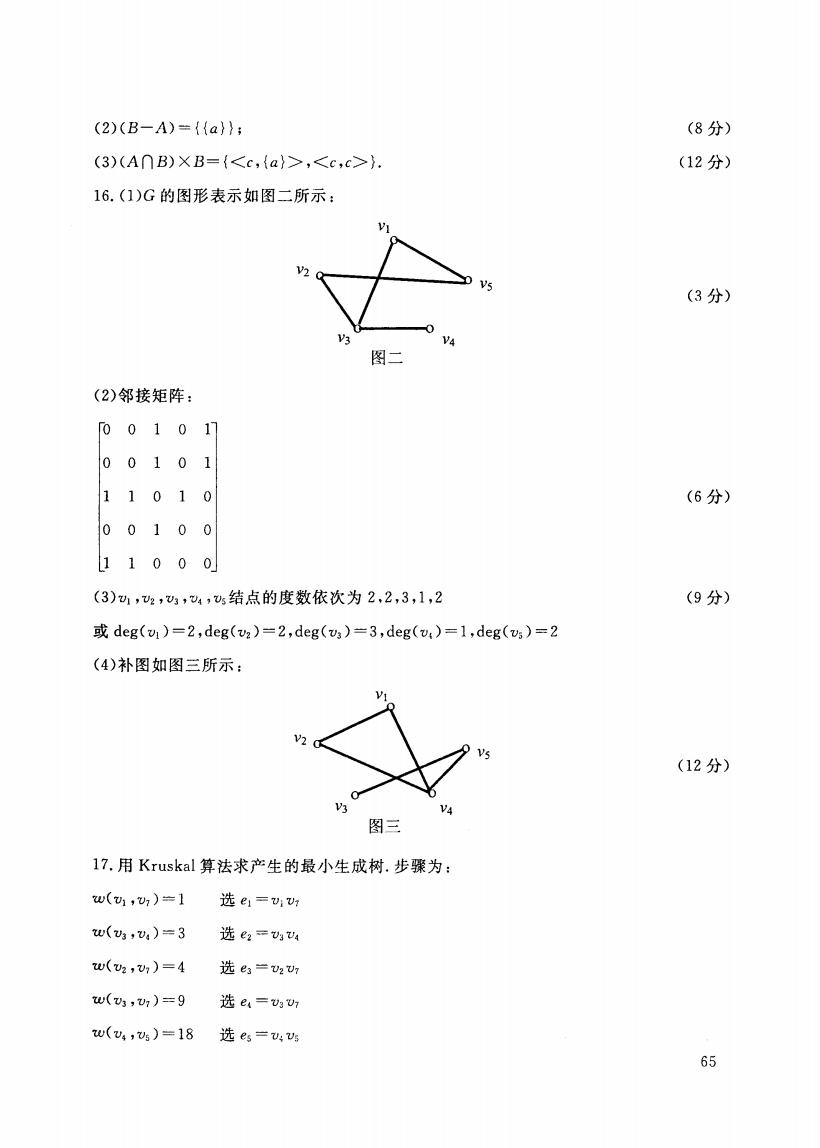
(2)(B-A)={a}: (8分) (3)(A∩B)XB={,). (12分) 16.(1)G的图形表示如图二所示: VI V2 (3分) 图二 (2)邻接矩阵: 0010 17 00101 11010 (6分) 0 0 100 1000 (3)1,2,,4,s结点的度数依次为2,2,3,1,2 (9分) deg(v)=2,deg(v2)=2,deg(va)=3,deg(v)=1,deg(vs)=2 (4)补图如图三所示: V2 (12分) 图三 17.用Kruskal算法求产生的最小生成树.步骤为: w(u1,w,)=1 选e1=:r w(3,v4)=3 选e2=v4 U(2,,)=4 选e3=v2 w(3,v)=9 选e(=Ugv7 w(u4,5)=18 选es=u:s 65
(2)(B-A) = {{a}}; (3)(An B) XB= { , }. 16. (1 的 图 VI (8 (1 V2 V5 (3 V3 图二 V4 (2) 邻接矩 阵 b 0 1 0 1 o 0 101 1 1 010 00100 1 1 000 (3)'0 1 结点 1, VI) = 2 , deg('02) = 2 , deg('03 ) = 3 , deg('04 ) = 1 , deg('05) = 2 (4) 三所 VI (6 (9 ν2 V5 (1 V3 图兰 V4 17. 用Kruskal 成树 W(VI ,v7)=1 =Vi '07 W(V3 叫 叫 W(V2 ,'07 ) =4 ='02'07 W( '0 =9 ='03'07 W(V ,vs)=18 选es '0 65

w(v1,V6)=22选e6=U16 (6分) 最小生成树如图四所示: (9分) s D 18 图四 最小生成树的权为:w(T)=22+1+4+9+3+18=57. (12分) 如果采用破圈法,可参照评分 六、证明题(本题共8分) 18.证明: (1)(A∧7B) P (1分) (2)-AVB T(1)E (3分) (3)(BVC) P (4分) (4)C 心 (5分) (5)B T(3)(4)1 (6分) (6)7A T(2)(5)I (8分) 说明: 1.因证明过程中,公式引用的次序可以不同,一般引用前提正确得1分,利用两个公式得 出有效结论得1或2分,最后得出结论得2或1分 2.可以用真值表验证, 66
P T (1)E P P T(3)(4 )I T(2)(5 )I W(VJ' 选e6 =Vj V6 最小生成树如图四所示: 18 图四 最小生成树的权为 如果采用破圈法,可参照评分. 六、证明题{本题共 8分) 18. (1) --, (A --' R) (2) --,A VB (3)( --, B VC) (4) --, C (5) --, B (6) --, A ,l' j (6 (9 (1 (1分) (3 (4 (5 (6 (8 说明 1.因证明过程中,公式引用的次序可以不同,一般引用前提正确得 1分,利用两个公式得 出有效结论得 2分,最后得出结论得 1分. 2. 66