
试卷代号:1009 座位■■ 中央广播电视大学2013-一2014学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本)试题 2014年1月 题 号 一 二 三 四 五 六 总分 分 数 得分 评卷人 一、单项选择题(每小题3分,本题共15分)】 1.若集合A={a,b,c》,则下列表述正确的是(). A.{a}∈A B.(a)CA C.0∈A D.{a,b,c}∈A 2.设A={1,2},B={1,2,3,4,5},A到B的关系R={(x,y》1x∈A,y∈B,x十1=y},则 R=(). A.{,} B.{,,,,} C.{,} D.{,} 3.无向图G的边数为12,则图G的结点的度数之和是( ) A.24 B.12 C.6 D.18 4.设连通平面图G有v个结点,e条边,r个面,则( ) A.v十e-r=2 B.r+v-e=2 C.v十e-r=4 D.+e-r=-4 5.设个体域D是整数集合,则命题Vx3y(x·y=y)的真值是( A.不确定 B.F C.T D.以上说法都不是 65
试卷代号 座位号 中央广播电视大学 3一 4学年度第一学期"开放本科"期未考试(半开卷) 离散数学(本)试题 2014 年1 !题号|一|二|三|四|五|六|总分| |分数 I I I I I I I I I 项选 每小 本题 1.若集合 {a c} 则下 ). A. {a} B. {a}CA C.0εA D. {a c} 2. A = {1 , 2} ,B = {1 2, 3, 4,时, A到 B的关系 ε B ,则 R=( ). A. {,} B. { , ,, ,} c. {,} D. { , } 3. 图G 边数 tl 图G 度数 ). A.24 C.6 B. 12 D.18 4. 通平 图G 个结 条边 ). A.v十e-r=2 C. v+e-r=4 B.r+v-e=2 D. v+e-r=-4 5. 个体域D 数集合 ). A. 不确定B.F CT 65

得分 评卷人 二、填空题(每小题3分,本题共15分) 6.设集合A={1,2,3},B={3,4,5},C={5,6,7},则AUB-C等于 7.设A={1,2},B={a,b},C={3,4,5},从A到B的函数f={,},从B 到C的函数g={,},则Ran(gf)等于 8.若图G=,其中V={a,b,c,d},E={(a,b),(a,d),(b,c),(b,d)》,则该图中的 割边为」 9.设G是欧拉图,则G的奇数度数的结点数为 个 10.设个体域D={2,4,6},A(x)为“x是偶数”,则谓词公式(x)A(x)的真值 为 得分 评卷人 三、逻辑公式翻译(每小题6分,本题共12分)】 11.将语句“我学英语,并且学法语.”翻译成命题公式 12.将语句“除非小王来,否则小李不去.”翻译成命题公式. 得 分 评卷人 四、判断说明题(每小题7分,本题共14分) 判断下列各题正误,并说明理由, 13.空集⑦的幂集也是空集. 14.(3x)(P(x)-→Q(y)∧R(z))中的约束变元为y. 得分 评卷人 五、计算题(每小题12分,本题共36分)】 15.设集合A={1,2,3},R={,,},S={,}试 计算: (1)R·S; (2)R-1;(3)r(R). 66
得分|评卷人 二、填空题{每小题 3分,本题共 5分} 6. 设集合 {l 3, 4, 时, {5 , 6, 7} ,则 B一 C等于 7. 3, 4, I, >, 2, }, C的函数 Of) 8. {a ,b, c, d },E = {(a ,(a ,d) ,(b ,(b ,d)} 割边为 9. 设G 是欧拉 则G 奇数 为一 10. 设个 体 域 词 公 V' |得分|评卷人| I I I 三、逻辑公式翻译{每小题 6分,本题共 2分} 1. 学英语 且学法 命题公 12. 非小 否则小 题公 |得分|评卷人| I I I 四、判断说明题{每小题 7分,本题共 4分} 判断下列各题正误,并说明理由. 13. 事集 14. (丑 x AR(z» 变元 |得分|评卷人| I I I 五、计算题{每小题 2分,本题共 6分} 15. A = {l, 2, 3},R = { , , }, 5= { , } 计算 (l)R • 5; (2)R- 1 ; (3)r(R). 66

16.图G=,其中V={a,b,c,d},E={(a,b),(a,c),(a,d),(b,c),(c,d)},对应 边的权值依次为6、5、2、3及8,试: (1)画出G的图形: (2)写出G的邻接矩阵; (3)求出G权最小的生成树及其权值. 17.试画一棵带权为1,2,3,3,4的最优二叉树,并计算该最优二叉树的权. 得分 评卷人 六、证明题(本题共8分) 18.试证明:P→Q→P→(PΛQ). 67
16. ,E= {(a ,b) , (a ,c) , (a ,d ), (b , c) , (c 边的权值依次为 6、 5、 2、 3及 8,试 (1)画出 G的图形 (2) 出G 邻接矩 (3) 出G 最小 17. 棵带 为1 ,2 ,3 ,3 ,4 优二 二叉 |得分|评卷人| I I I 六、证明题{本题共 18. 67

试卷代号:1009 中央广播电视大学2013一2014学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本)试题答案及评分标准 (供参考) 2014年1月 一、单项选择题(每小题3分,本题共15分) 1.B 2.D 3.A 4.B 5.c 二、填空题(每小题3分,本题共15分)》 6.{1,2,3,4} 7.{3,4} 8.(b,c) 9.0 10.真(或T,或1) 三、逻辑公式翻译(每小题6分,本题共12分) 11.设P我学英语,Q:我学法语, (2分) 则命题公式为:P∧Q, (6分) 12.设P:小王来,Q:小李去. (2分) 则命题公式为:Q→P. (6分) 或P+一Q 四、判断说明题(每小题7分,本题共14分) 13.错误. 3分) 空集的幂集为{☑}. (7分) 14.错误, (3分) (3x)(P(x)+Q(y)∧R(z))中的约束变元为x. (7分) 五、计算题(每小题12分,本题共36分) 15.(1)R·S=={,,}; (4分) 68
试卷代号 0 0 中央广播电视大学 4学年度第一学期"开放本科"期末考试{半开卷) 离散数学(本)试题答案及评分标准 (供参考〉 2014 年1 一、单项选择题{每小题 3分,本题共 5分) l. B 2.D 3.A 4.B 5. C 二、填空题{每小题 3分,本题共 5分} 6. {1 ,2 ,3 ,4} 7. {3 ,4} 8. (h ,c) 9.0 10. 或T 1) 三、逻辑公式翻译{每小题6分,本题共 2分} 1 1. 设P: 英语 学法 则命题公式为 I\ Q. 12. 则命题公式为 或-,P→-, 四、判断说明题{每小题 7分,本题共 4分} 13. 空集的事集为{臼} . 14. (丑 (P(x) 为x. 五、计算题{每小题 2分,本题共 6分} 15. (1)R · S=={, ,}; 68 (2 (6 (2 (6 (7 (3 (7 (4
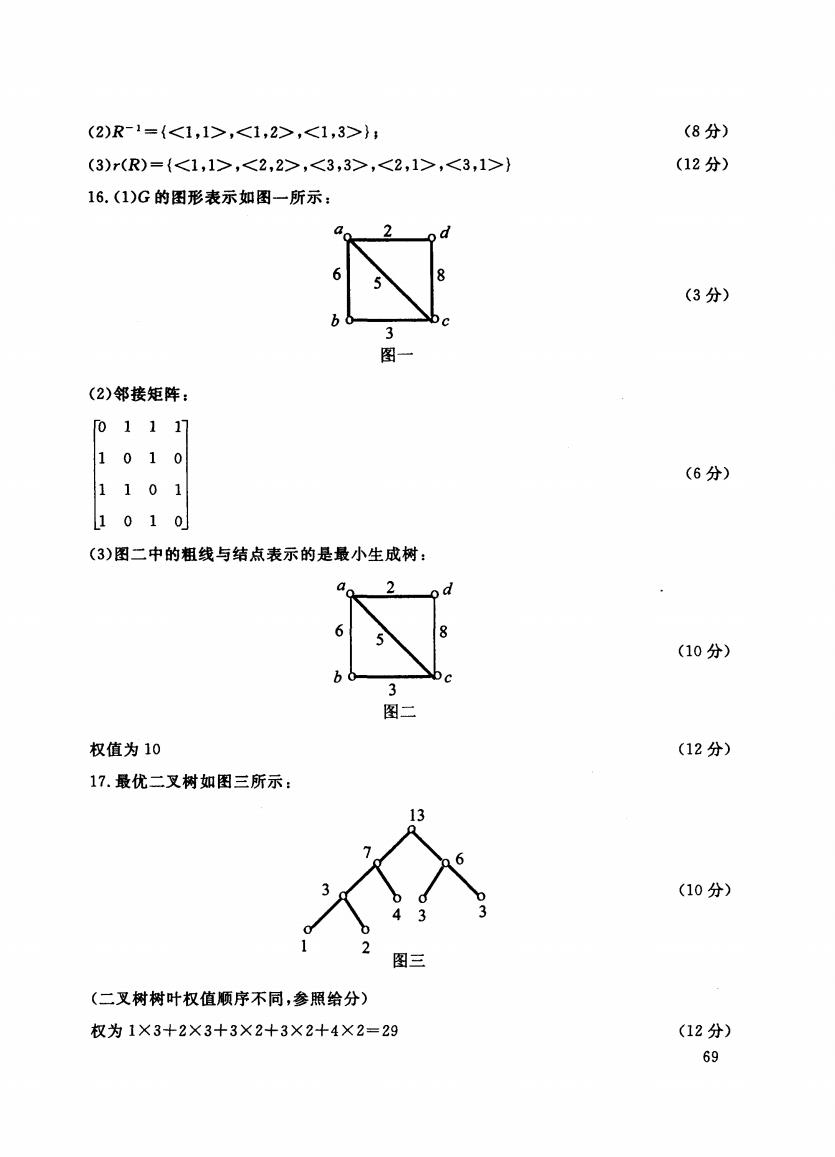
(2)R-1={,,}: (8分) (3)r(R)={,,,,} (12分) 16.(1)G的图形表示如图一所示: 0 2 d 6 8 5 (3分) 3 图一 (2)邻接矩阵: 01117 1010 (6分) 1101 1010 (3)图二中的粗线与结点表示的是最小生成树: a 6 5 (10分) b 3 图二 权值为10 (12分) 17.最优二叉树如图三所示: 13 7 3 ● (10分) 图三 (二叉树树叶权值顺序不同,参照给分) 权为1×3+2×3+3×2+3×2+4×2=29 (12分) 69
(2)R- 1 = {, , }I (3)r(R) = {, , , , } (8 (1 16. (l) 示如 一所 G6b d8c (3 图一 (2) 接矩 b 1 1 1 101 0 1 101 1 0 1 0 (6 (3) 是最小生成树 d8c (1 权值为 17. 优二 三所 (1 2 13 (1 (二叉树树叶权值顺序不同,参照给分〉 权为 (1 69

六、证明题(本题共8分) 18.证明: (1)P+Q P (1分) (2)P P(附加前提) (3分) (3)Q T(1)(2)I (5分) (4)PΛQ T(2)(3)I (7分) (5)P→(PΛQ) CP规则 (8分) 另证: 设P+(P∧Q)为F, (1分) 则P为T,PAQ为F, (3分) 所以P为T,Q为F, (5分) 从而P→Q也为F (7分) 所以P→Q→P→(P∧Q) (8分) 说明:1.因证明过程中,公式引用的次序可以不同,一般引用前提正确得1分,利用两个公 式得出有效结论得1或2分,最后得出结论得2或1分. 2.可以用真值表验证. 70
六、证明题{本题共 8分} 18. (l)P• Q (2)P (3)Q (4)PAQ (5)P• (P A Q) 另证 )为 F 所以 从而 Q也为 所以 Q=争 P P( 前提 T (l)(2)l T(2)(3 )l CP (l分〉 (3 (5 (7 (8 (l分〉 (3 (5 (7 (8 说明:1.因证明过程中,公式引用的次序可以不同,一般引用前提正确得1分,利用两个公 式得出有效结论得 2分,最后得出结论得 1分. 2. 表验 70