
试卷代号:1009 座位号■■ 国家开放大学(中央广播电视大学)2014年秋季学期“开放本科”期末考试 离散数学(本)试题(半开卷) 2015年1月 题 号 二 三 四 五 六 总 分 分 数 得分 评卷人 一、单项选择题(每小题3分,本题共15分) 1.若集合A={b,c,d},则下列表述正确的是(). A.{b,c,d}∈A B.A∈{c,d} C.(b,c,d)CA D.(b,c)CA 011001 10010 2.已知无向图G的邻接矩阵为 10011 ,则G有( 0110 1 0 011 0 A.6点,10边 B.5点,12边 C.6点,5边 D.5点,6边 3.无向图G是个棵树,结点数为10,则G的边数是(). A.9 B.10 C.11 D.12 4.设A(x):x是人,B(x):x是工人,则命题“有人是工人”可符号化为(), A.(Yx)(A(x)AB(x)) B.(x)(A(x)→B(x) C.(3x)(A(x)AB(z)) D.(3x)(A(x)B(x) 5.下面的推理正确的是(). A.(1)(x)F(x)+G(x) 前提引人B.(1)(Hx)(F(x)+G(x) 前提引入 (2)F(y)→G(y) US(1). (2)F(y)→G(y) US(1). C.(1)(3x)F(x)→G(x) 前提引人D.(1)(3x)(F(x)→G(x) 前提引人 (2)F(y)→G(y) US(1). (2)F(y)+G(x) ES(1). 80
试卷代号 :1009 座位号 80 国家开放大学(中央广播电视大学)2014 年秋季学期"开放本科"期末考试 离散数学(本) 试题(半开卷) 2015 E 一、单项选择题{每小题 分,本题共 15 分} 1.若集合 A= {b d} 则下列表述正确的是( ). A. {b d} εA B.AC{c ,d} C. {b ,c.d}CA D. 怡,c} CA Ò 1 1 0 0 10010 已知元向图 的邻接矩阵为 11 0 0 1 11 ,则 有( ) o 1 101 00110 A.6 点, 10 B.5 点, 12 C.6 点, D.5 点, 3. 无向图 是个棵树,结点数为 10 ,Þltl 的边数是( ). A.9 B. 10 C.11 D.12 4. A(x) :x 是人 B(x) :x 是工人,则命题"有人是工人"可符号化为( ). A. ( 't/ x) (A(x) ^ B(x)) B. .., (\1'x)(A(x)• B(x)) c. ( 3 x)(A(x) B(x)) D. .., ( 3 x)(A(x) 八.., B(x)) 5. 下面的推理正确的是( A. (1)(\1' x) F(x)• G(x) 前提引人 B. (1)(\1'x)(F(x)• G(x)) (2)F(y)• G(y) US (l). (2)F(y)• G(y) C. (1)( 3x)F(x)• G(x) 前提引人 D. (1)( 3x)(F(x)• G(x)) (2)F(y)• G(y) US( 1). (2)F(y)• G(x) 前提引人 US( 1). 前提引人 ES(1)

得分 评卷人 二、填空题(每小题3分,本题共15分) 6.设A={a,b,c},B={1,2,3},作f:A→B,则不同的函数个数为 7.任一无向图中,度数为奇数的结点的个数为· 8.设G是汉密尔顿图,S是其结点集的一个子集,若S的元素个数为6,则在G-S中的连 通分支数不超过 9.设G是有8个结点的连通图,结点的度数之和为28,则可从G中删去 条边后 使之变成树. 10.设个体域D={1,2},则谓词公式(x)P(x)V(3x)Q(x)消去量词后的等值式 为 得分 评卷人 三、逻辑公式翻译(每小题6分,本题共12分) 11.将语句“小张和小李都可以完成这项工作”翻译成命题公式. 12.将语句“a是偶数当且仅当a能被2整除.”翻译成命题公式. 得 分 评卷人 四、判断说明题(每小题7分,本题共14分)】 判断下列各题正误,并说明理由, 13.存在集合A与B,使得A∈B与A二B同时成立. 14.完全图Ks是平面图. 81
|得分|评卷人| | 二、填空题{每小题 分,本题共 15 分} 6. A= ,c} ,B= {1 3} ,作 !:A 则不同的函数个数为一一-一一- 7. 任一元向图中,度数为奇数的结点的个数为一一一-- 8. 是汉密尔顿图, 是其结点集的一个子集,若 的元素个数为 ,则在 G-5 中的连 通分支数不超过--一一一 9. 是有 个结点的连通图,结点的度数之和为 28 ,则可从 中删去 条边后 使之变成树. 10. 设个体域 D= {1, 2} 则谓词公式 Cltx)P(x) V (3x)Q(x) 消去量词后的等值式 |得分 评卷人| | 三、逻辑公式翻译(每小题 分,本题共 12 分) 1.将语句"小张和小李都可以完成这项工作"翻译成命题公式. 12. 将语句"α 是偶数当且仅当 能被 整除"翻译成命题公式. 四、判断说明题(每小题 分,本题共 14 分) 判断下列各题正误,并说明理由. 13. 存在集合 B. 使得 AεB 与 ACB 同时成立. 14. 完全图 Ks 是平面图. 81

得分 评卷人 五、计算题(每小题12分,本题共36分)】 15.设A={2,3,6,12,24,36},B为A的子集,其中B={6,12},R是A上的整除关 系,试: (1)写出R的关系表达式; (2)说明R为偏序关系; (3)画出关系R的哈斯图: (4)求出B的最大元素、极大元素、上确界. 16.设图G=,V={,2,3,4,},E={(v,2),(1,3),(,5),(,), (2,4),(2,v5),(3,4),(3,u),(04,5)},试: (1)画出G的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出图G的补图的图形 17.求P→(QAR)的合取范式与主合取范式. 得 分 评卷人 六、证明题(本题共8分)】 18.对任意集合A,B和C,若有C≠⑦,则有:A二B的充分必要条件是C×A二C×B. 82
五、计算题{每小题 12 分,本题共 36 分) 15. = {2 , 3 , 6 , 12 , 24 , 36} , 的子集,其中 B={6 12} 上的整除关 系,试: (1)写出 的关系表达式; (2) 说明 为偏序关系; (3) 画出关系 的哈斯图; (4) 求出 的最大元素、极大元素、上确界. 16. 设图 G= V={Vj' V3 V5 } , E = { ( Vj ) , (Vj , V3 ) , (V, 'Vs ) , (屿 V3) , (V2 V4) (V2 V5)'( V4) , ( V3 , Vs ) , (V4 ,V5 ) } ,试; (1)画出 的图形表示; (2) 写出其邻接矩阵; (3) 求出每个结点的度数; . (4) 画出图 的补图的图形. 17. (Q R) 的合取范式与主合取范式. 六、证明题{本题共 分} 18. 对任意集合 ,若有 ,则有 :ACB 的充分必要条件是 CXACCXB. 82

试卷代号:1009 国家开放大学(中央广播电视大学)2014年秋季学期“开放本科”期末考试 离散数学(本)试题答案及评分标准(半开卷) (供参考) 2015年1月 一、单项选择题(每小题3分,本题共15分) 1.D 2.D 3.A 4.C 5.B 二、填空题(每小题3分,本题共15分) 6.27 7.偶数 8.6 9.7 10.(P(1)∧P(2))V(Q(1)VQ(2) 三、逻辑公式翻译(每小题6分,本题共12分) 11.设P:小张可以完成这项工作,Q:小李可以完成这项工作. (2分) 则命题公式为:P∧Q. (6分) 12.设P:a是偶数,Q:a能被2整除, (2分) 则命题公式为:P←+Q (6分) 四、判断说明题(每小题7分,本题共14分) 13.正确、 (3分) 例:设A={a},B={a,{a} (5分) 则有A∈B且A二B. (7分) 说明:举出符合条件的例均给分 14.错误. (3分) 完全图Ks是有5个结点10条边,因3×5一6,,,,,,,, 83
试卷代号 :1009 国家开放大学(中央广播电视大学 )2014 年秋季学期"开放本科"期末考试 离散数学(本) 试题答案及评分标准(半开卷) (供参考) 一、单项选择题(每小题 分,本题共 15 分) l. D 2.D 3. A 二、填空题{每小题 分,本题共 15 分} 6.27 7. 偶数 8.6 9. 7 10. (P (1) P(2)) V (Q(1) VQ(2)) 三、逻辑公式翻译{每小题 分,本题共 12 分} 4.C 1.设 P: 小张可以完成这项工作 Q: 小李可以完成这项工作. 则命题公式为 :P Q. 12. P:a 是偶数 Q: 能被 整除. 则命题公式为 :p.-..Q. 四、判断说明题{每小题 分,本题共 14 分) 5. B 2015 (2 分〉 (6 分) (2 分) (6 分〉 13. 正确 (3 分) 例:设 A={ B= {a}} (5 分〉 则有 AεB ACB. (7 分) 说明:举出符合条件的例均给分. 14. 错误 (3 分) 完全图 Ks 是有 个结点 10 条边,因 3X5-6 , , , , , , , , 83
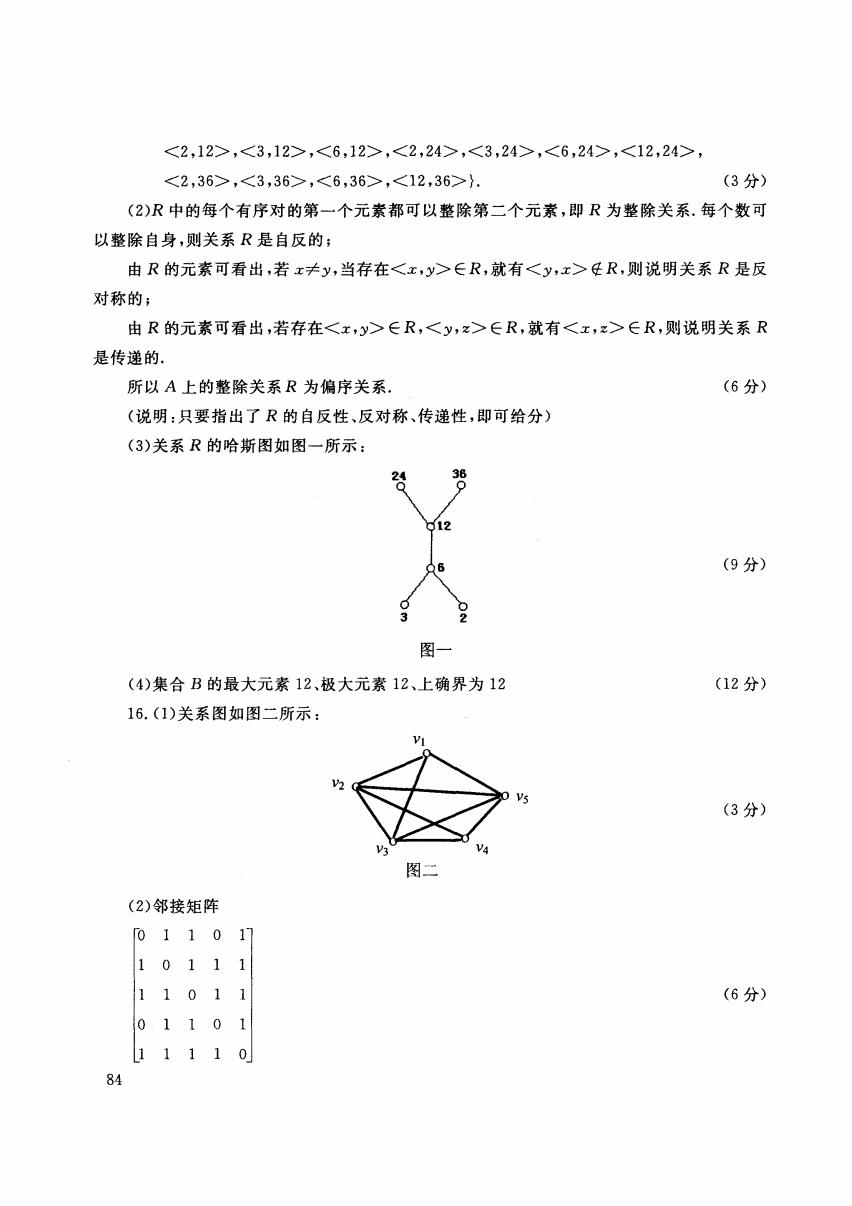
,,,,,,, ,,,}. (3分) (2)R中的每个有序对的第一个元素都可以整除第二个元素,即R为整除关系.每个数可 以整除自身,则关系R是自反的; 由R的元素可看出,若x≠y,当存在∈R,就有任R,则说明关系R是反 对称的; 由R的元素可看出,若存在∈R,∈R,就有∈R,则说明关系R 是传递的, 所以A上的整除关系R为偏序关系. (6分) (说明:只要指出了R的自反性、反对称、传递性,即可给分) (3)关系R的哈斯图如图一所示: 12 06 (9分) 图一 (4)集合B的最大元素12、极大元素12、上确界为12 (12分) 16.(1)关系图如图二所示: (3分) V3 图二 (2)邻接矩阵 011011 10111 11011 (6分) 01101 11110 84
, , , , , , , , , ,}. (3 分〉 (2)R 中的每个有序对的第一个元素都可以整除第二个元素,即 为整除关系.每个数可 以整除自身,则关系 是自反的; 的元素可看出,若 当存在 就有 f!: 则说明关系 是反 对称的; 的元素可看出,若存在ER 就有 则说明关系 是传递的. 84 所以 上的整除关系 为偏序关系. (说明:只要指出了 的自反性、反对称、传递性,即可给分) (3) 关系 的哈斯图如图一所示: 24 36 3 2 图一 (4) 集合 的最大元素 12 、极大元素 12 、上确界为 12 16. (1)关系图如图二所示: (2) 邻接矩阵 o 1 101 10111 1 101 1 o 1 101 11110 V2 Vl 图二 Vs (6 分) (9 分) (1 分) (3 分) (6 分)

(3)deg(v1)=3 deg(2)=4 deg(v3)=4 deg(v)=3 deg(vs)=4 (9分) (4)补图如图三所示: Q V20 0v5 (12分) 50 图三 17.P→(Q∧R) PV(Q∧R) (2分) (PVQ)A(PVR)合取范式 (5分) (-PVQ)V(R∧-R)A(PVR) (7分) =(-PVQ)V(RAR)∧(-PVR)V(QA→Q) (9分) (PVQVR)A(PVQV-R)A(-PVRVQ)A(-PVRV-Q) (11分) ÷-PVQVR)∧(-PVQV-R)A(PV-QVR) 主合取范式 (12分) 六、证明题(本题共8分) 18.证明: 已知C≠0,即存在c∈C, 设A三B,则对任意∈CXA,有c∈C,a∈A, (1分) 可得c∈C,a∈B, (2分) 即有∈CXB, (3分) 所以CXA二CXB. (4分) 再设CXA二CXB, 则对任意a∈A,由∈CXA可得∈CXB, (5分) 即有c∈C,a∈B, (6分) 所以A二B, (7分) 得证. (8分) 85
(3)deg(Vl)=3 deg( vz) =4 deg(V3) =4 deg( )=3 deg( Vs) =4 (4) 补图如图三所示: 17. (Q R) 。..., PV (Q^R) V20 V30 。(..., PV Q) 八(..., PV R) 合取范式 。(..., PVQ) V (R八...,R)八(..., PV R) Vl \ 图二 (..., p V Q) V (R ^...,R) (-.P V R) V (Q ^ ...,Q) o Vs V4 (..., P V QV R) (..., V QV ...,R)八(..., PV RVQ) (..., V R V ...,Q) 。(..., PVQVR) (..., V Q V ...,R) ^ (...,p V ...,Q V R) 六、证明题(本题共 分} 18. 证明 已知 ,即存在 cεC ACB 则对任意 CXA cε εA 可得 cε aEB 即有 εCXB 所以 CXACCXB. 再设 CXACCXB 主合取范式 则对任意 aεA ,由 ECXA 可得 εCXB 即有 cε εB 所以 ACB 得证. (9 分〉 (1 分) (2 分) (5 分) (7 分) (9 分) (11 分) (1 2 分) (1分) (2 分) (3 分) (4 分) (5 分) (6 分) (7分) (8 分) 85