
试卷代号:1009 座位号■■ 国家开放大学(中央广播电视大学)2015年春季学期“开放本科”期末考试 离散数学(本)试题(半开卷)】 2015年7月 题 号 二 三 四 五 六 总 分 分 数 得 分 评卷人 一、单项选择题(每小题3分,本题共15分) 1.若集合A={1,2,3},则下列表述正确的是(). A.{1,2,3}∈A B.AC{1,2} C.{1,2,3}二A D.{1,2}∈A 2.已知无向图G有10条边,则G的结点度数之和为(). A.10 B.20 C.30 D.5 3.无向图G是棵树,边数为10,则G的结点数是( A.5 B.10 C.9 D.11 4.设A(x):x是金属,B(x):x是金子,则命题“有的金属是金子”可符号化为(). A.(3 x)(A(x)AB(x)) B.(Hx)(A(x)→B(x) C.(Y x)(A(x)AB(z)) D.7(3x)(A(x)∧B(x)) 5.下面的推理正确的是( ) A.(1)(Hx)F(x)+G(x) 前提引人B.(1)(3x)F(x)+G(x) 前提引人 (2)F(y)→G(y) US(1) (2)F(y)+G(y) US(1) C.(1)(3x)(F(x)→G(x)) 前提引人D.(1)(]x)(F(x)+G(x)) 前提引人 (2)F(y)+G(y) ES(1) (2)F(y)+G(x) ES(1) 89
试卷代号 :1009 座位号仁口 国家开放大学(中央广播电视大学)2015 年春季学期"开放本科"期末考试 离散数学(本) 试题(半开卷} 2015 一、单项选择题{每小题 分,本题共 15 分} 1.若集合 A= {l, 3} 则下列表述正确的是( ). A. {1 ,2 3}εA B. AC{l ,2} c. {l, 2 , 3 } cA D. {l, 2}εA 2. 已知无向图 10 条边,则 的结点度数之和为( ). A.10 B.20 C.30 D.5 3. 元向图 是棵树,边数为 10 ,则 的结点数是( ). A.5 B.10 C. 9 D. 11 4. A(x) :x 是金属 B(x) :x 是金子,则命题"有的金属是金子"可符号化为( ). A. ( 3 x)(A(x) B(x)) c. ( V x) (A(x) B(x)) 5. 下面的推理正确的是( ). A. (1)( V x)F(x)• G(x) (2)F(y)• G(y) B.寸 (V x)(A(x)• B(x)) D. 寸(丑 x)(A(x) ^ -, B(x)) 前提引人 B. (1)( 3 x)F(x)• G(x) US(1) (2)F(y)• G(y) 前提引人 US(1) C. (1)( 3 x)(F(x)• G(x)) 前提引人 D. (1) ( 3 x)(F(x)• G(x)) 前提引入 (2)F(y)• G(y) ES(1) (2)F(y)• G(x) ES(I) 89

得分 评卷人 二、填空题(每小题3分,本题共15分) 6.设A={1,2},B={a,b,c},作f:A→B,则不同的函数个数为 7.有n个结点的无向完全图的边数为 8.设无向图G中存在欧拉回路,则G的奇数度数的结点数为 个. 9.设G是有8个结点的连通图,结点的度数之和为24,则可从G中删去 条边后使之变成树, 10.设个体域D={a,b,c},则谓词公式(Hx)A(x)消去量词后的等值式为 得 分 评卷人 三、逻辑公式翻译(每小题6分,本题共12分) 11.将语句“学生的主要任务是学习”翻译成命题公式. 12.将语句“我们下午2点或者去礼堂看电影或者去教室看书.”翻译成命题公式· 得 分 评卷人 四、判断说明题(判断各题正误,并说明理由。每小题7分,本题共 14分) 13.不存在集合A与B,使得A∈B与A二B同时成立. 14.完全图K4(如下图)是平面图. 得 分 评卷人 五、计算题(每小题12分,本题共36分)】 15.设偏序集的哈斯图如下图所示,B为A的子集,其中B={a,b,c},试 (1)写出R的关系表达式: (2)画出关系R的关系图; 90
|得分|评卷人| | 二、填空题{每小题 分,本题共 15 分} 6. A= {1 , 2} ,B= {a 叶,作 /:A 则不同的函数个数为 7. 个结点的无向完全图的边数为 8. 设元向图 中存在欧拉回路,则 的奇数度数的结点数为 个. 9. 是有 个结点的连通,图,结点的度数之和为 24 ,则可从 中删去 条边后使之变成树. 10. 设个体域 D={a ,c} 则谓词公式(V x)A(x) 消去量词后的等值式为 三、逻辑公式翻译{每小题 分,本题共 12 分} 1.将语句"学生的主要任务是学习"翻译成命题公式. 12. 将语句"我们下午 点或者去礼堂看电影或者去教室看书"翻译成命题公式. |得分|评卷人| | 四、判断说明题{判断备题正误,并说明理由。每小题 分,本题共 14 分} 13. 不存在集合 使得 AεB ACB 同时成立. 14. 完全图 如下图〉是平面图. |得分|评卷人| | 五、计算题{每小题 12 分,本题共 36 分} 90 15. 设偏序集 的哈斯图如下图所示 的子集,其中 B= {a ,c}, (1)写出 的关系表达式; (2) 画出关系 的关系图;

(3)求出B的最大元素、极小元素、上界. d b 16.设图G=,V={v1,2,34,5},E={(01,2),(0,),(U,5),(v2,u), (,s)},试 (1)画出G的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出图G的补图的图形, 17.求P→(Q∧R)的析取范式与主合取范式. 得分 评卷人 六、证明题(本题共8分】 18.设A,B,C均为任意集合,试证明:A∩(B-C)=(A∩B)-(A∩C). 91
(3) 求出 的最大元素、极小元素、上界. d b C 1U((((1 E U U U U U U U U U |得分|评卷人| | 六、证明题{本题共 分} 18. A.B.C 均为任意集合,试证明 :A (B-C)=(AnB) (An C). 91

试卷代号:1009 国家开放大学(中央广播电视大学)2015年春季学期“开放本科”期末考试 离散数学(本) 试题答案及评分标准(半开卷) (供参考) 2015年7月 一、单项选择题(每小题3分,本题共15分】 1.C 2.B 3.D 4.A 5.C 二、填空题(每小题3分,本题共15分)】 6.9 7.n(n-1)/2 8.0 9.5 10.A(a)∧A(b)∧A(c) 三、逻辑公式翻译(每小题6分,本题共12分) 11.设P:学生的主要任务是学习. (2分) 则命题公式为:P. (6分) 12.设P:我们下午2点去礼堂看电影, Q:我们下午2点去教室看书· (2分) 则命题公式为:一(P+Q) (6分) 注:或者(P∧Q)V(PA-Q) 四、判断说明题(每小题7分,本题共14分) 13.错误. (3分) 例:设A={a},B={a,{a} (5分) 则有A∈B且A二B. (7分) 说明:举出符合条件的反例均给分· 14.正确. (3分) 完全图K,是平面图, (5分) 92
试卷代号 :1009 国家开放大学(中央广播电视大学 )2015 年春季学期"开放本科"期末考试 离散数学(本) 试题答案及评分标准(半开卷) (供参考) -、单项选择题{每小题 分,本题共 15 分} l. C 2. B 3. D 二、填空题{每小题 分,本题共 15 分} 6.9 7.n(n 1)/2 8.0 9.5 10. A(a) A(b) A(c) 三、逻辑公式翻译{每小题 分,本题共 12 分} 1.设 P: 学生的主要任务是学习. 则命题公式为 :P. 12. P: 我们下午 点去礼堂看电影, 也我们下午 点去教室看书. 则命题公式为 :--, (p......Q). 注:或者 (-, Q) V (P ^ -,Q) 四、判断说明题(每小题 分,本题共 14 分} 13. 错误. 92 例:设 A={a} B= 忡,{ a} } 则有 AεB ACB. 说明:举出符合条件的反例均给分- 14. 正确. 完全图 K4 是平面图, 4.A 5. C 2015 (2 分〉 (6 分) (2 分) (6 分) (3 分) (5 分) (7分〉 (3 分) (5 分)
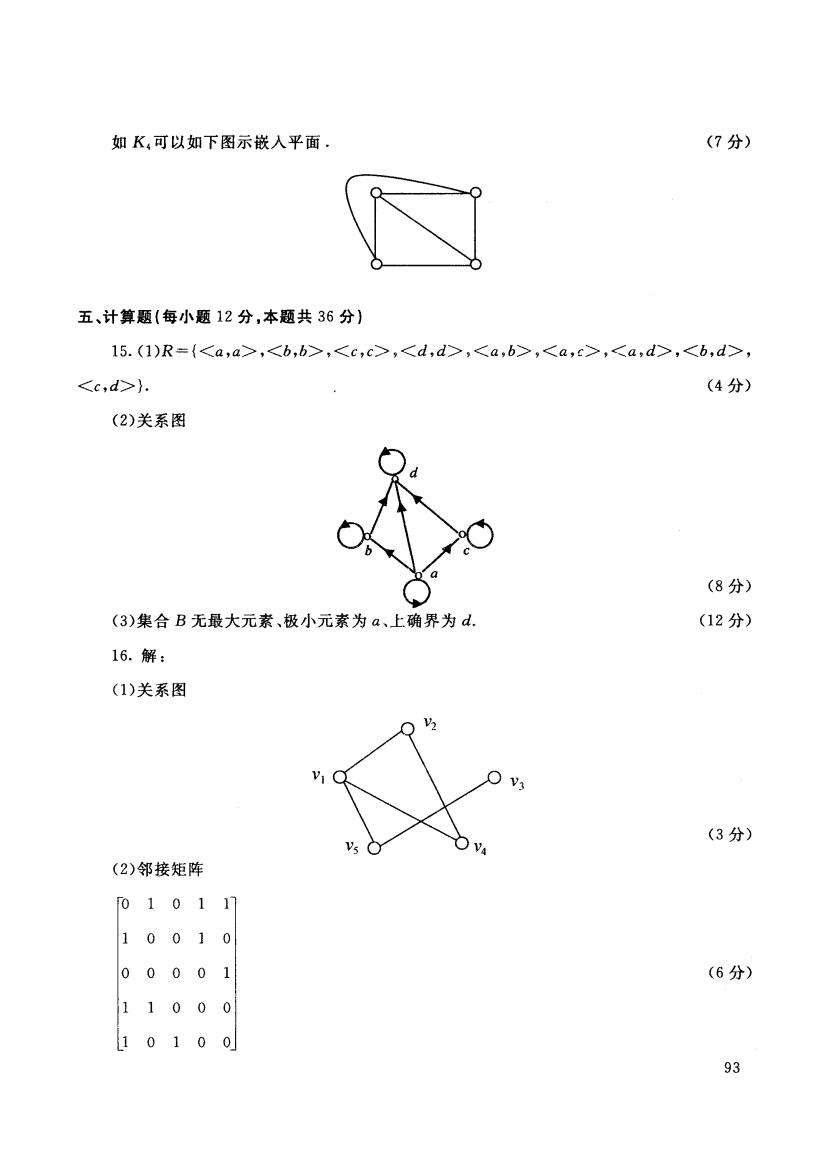
如K,可以如下图示嵌入平面. (7分) 五、计算题(每小题12分,本题共36分) 15.(1)R={,,,,,,,, }. (4分) (2)关系图 (8分) (3)集合B无最大元素、极小元素为a、上确界为d. (12分) 16.解: (1)关系图 (3分) (2)邻接矩阵 010117 0 1001 000.01 (6分) 1100 0 10100 93
K4 可以如下图示嵌入平面. (7 分〉 五、计算题{每小题 12 分,本题共 36 分) 15. (l )R={ . c>. , }. (2) 关系图 (3) 集合 元最大元素、极小元素为 、上确界为 d. 16. 解: (1)关系图 (2) 邻接矩阵 o 1 0 1 1 10010 o 0 0 0 1 1 1 000 II 0 1 0 0 V1 ν3 (4 分) (8 分) (1 2 分) (3 分〉 (6 分) 93

(3)deg(v1)=3 deg(v2)=2 deg(v3)=1 deg(v)=2 deg(vs )=2 (9分) (4)补图 (12分) 17.P-(QAR) PV(Q∧R)析取范式 (2分) PVQ)A(PVR) (5分) ÷(PVQ)V(RAR)∧(=PVR) (7分) (-PVQ)V(RA-R)A(-PVR)V(QA-Q) (9分) (PVQVR)A(-PVQV-R)A(-PVRVQ)A(-PVRV-Q) (11分) (-PVQVR)∧(-PVQV-R)∧(-PV-QVR) 主合取范式 (12分) 六、证明题(本题共8分)】 18.证明: 设S=A∩(B-C),T=(A∩B)-(A∩C) 若x∈S,则x∈A且x∈B一C,即x∈A,并且x∈B且xgC, (2分) 所以x∈(A∩B)且x(A∩C),得x∈T, (3分) 所以S三T. (4分) 反之,若x∈T,则x∈(A∩B)且xE(A∩C), (5分) 即x∈A,x∈B,且xgC,则得x∈B一C, (6分) 即得x∈A∩(B一C),即x∈S,所以T二S. (7分) 因此T=S. (8分) 另,可以用恒等式替换的方法证明, 94
(3)deg( Vl) = 3 deg( V2) =2 deg( )=1 deg( )=2 deg( )=2 (4) 00 170 (Q 八 R) ~PV (Q^ 的析取范式 (-.P V Q) 八(...., PV R) V1 (...., P V Q) V (R ^ ....,R) ^ (-,P V R) 。(-,PVQ) V (R 八-,R).^ (--,P V R) V (Q ^ -,Q) V3 (, V QV R) ^ (....,P V QV -,R) ^ (...,PV RV Q) ^ (-,P V R V ....,Q) (-,P V QV R) 八(-、PVQV -,R)八(-, PV ...., QVR) 主合取范式 六、证明题(本题共 分} 18。证明 94 S=An (B- C) , T=(A B) -(A C) , xES zεA xEB-C xEA 并且 xEB e;C , 所以 xE (Anm ~(A C) ,得 zε 所以 SCT. 反之,若 xET xE (An B) e; (AnC) , zξ A xEB e; 则得 zε B-C 即得 zε Ar (B-C) ,所以 TCS. 因此 T=S. 另,可以用恒等式替换的方法证明. (9 分) (1 分) (2 分) (5 分) (7 分) (9 分〉 (1 分) (1 分) (2 分) (3 分) (4 分〉 (5 分) (6 分) (7 分〉 (8 分)