
第2课时补集 课后·训练提升 基础巩固 1.若全集U={0,1,2,3},且Cu4={2;,则集合A的真子集共有( A.3个 B.5个 C.7个 D.8个 解析:由题意,得A={0,1,3},故A的真子集有231=7(个) 答案:C 2.己知全集U=R集合A={-1,0,1},B={xx2-2x=0},则图中的阴影部分表示的集合 为() A.{-1} B.{2} C.{1,2} D.{0,2} 解析:由已知,得B={0,2} 图中阴影部分对应的集合为B∩(CuA)={0,2}∩{xx≠-1,且x0,且≠1}={2} 答案B 3.已知全集U={x-11. 又A是U的子集, 所以12) 解析:,CRB={xx≤1或x≥2},又AU(RB)=R
第 2 课时 补集 课后· 基础巩固 1.若全集 U={0,1,2,3},且∁UA={2},则集合 A 的真子集共有( ) A.3 个 B.5 个 C.7 个 D.8 个 解析:由题意,得 A={0,1,3},故 A 的真子集有 2 3 -1=7(个). 答案:C 2.已知全集 U=R,集合 A={-1,0,1},B={x|x2 -2x=0},则图中的阴影部分表示的集合 为( ) A.{-1} B.{2} C.{1,2} D.{0,2} 解析:由已知,得 B={0,2}. 图中阴影部分对应的集合为 B∩(∁UA)={0,2}∩{x|x≠-1,且 x≠0,且 x≠1}={2}. 答案:B 3.已知全集 U={x|-11. 又 A 是 U 的子集, 所以 12} 解析:∵∁RB={x|x≤1 或 x≥2},又 A∪(∁RB)=R

.a≥2. 答案C 6.设S={1,2,3,4},且M={x∈Sr2-5x+p=0}.若CsM={1,4},则p=」 解析:S={1,2,3,4),CsM={1,4} ∴.M={2,3},即2,3是方程x2-5x+p=0的两根, p=2×3=6. 答案:6 7.设全集U=R,集合A={xx≥0},B={yy≥1},则CA与CuB的包含关系 是 解析:CA={xr<0},CB={yy<1}={xr<1} 故CUASCUB(或CUAECUB), 答案:CUASCUB(或CUAECuB) 8.设M,P是两个非空集合,定义M与P的差集为:MP={xx∈M,且xEP},则集合 M-(M-P)= 解析:根据定义“x∈M且xEP等价于“x∈M∩(CP)” 为此引入全集U,则MP=M∩(CP) 于是有M-(M-P)=M-[Mn(CuP)]=Mn{CU[Mn(CuP]}=Mn{(CuM)U [Cu(CUP)])=Mn[(CUM)U P]=[MO(CUM)]U(MOP)=U(MOP)=MOP.() M-P(M-(MIP) 答案:MnP 9.设U=R,已知集合A={x-5<x<5},B={x0≤x<7}, 求:(1)AnB;(2)AUB:(3)AU(CvB) (4)Bn(CUA);(5)(CUA)(CUB). 解:如图① (1)AnB={x0≤x<5} (2)AUB={x-5<x<7}. 图① 图② (3)如图② CuB={xr<0或x≥T}, .AU(CuB)={xx<5或x≥7} (4)如图③
∴a≥2. 答案:C 6.设 S={1,2,3,4},且 M={x∈S|x2 -5x+p=0}.若∁SM={1,4},则 p= . 解析:∵S={1,2,3,4},∁SM={1,4}, ∴M={2,3},即 2,3 是方程 x 2 -5x+p=0 的两根, ∴p=2×3=6. 答案:6 7.设全集 U=R,集合 A={x|x≥0},B={y|y≥1},则∁UA 与∁UB 的包含关系 是 . 解析:∁UA={x|x<0},∁UB={y|y<1}={x|x<1}. 故∁UA⫋∁UB(或∁UA⊆∁UB). 答案:∁UA⫋∁UB(或∁UA⊆∁UB) 8.设 M,P 是两个非空集合,定义 M 与 P 的差集为:M-P={x|x∈M,且 x∉P},则集合 M-(M-P)= . 解析:根据定义“x∈M,且 x∉P”等价于“x∈M∩(∁UP)”. 为此引入全集 U,则 M-P=M∩(∁UP). 于是有 M-(M-P)=M-[M∩(∁UP)]=M∩{∁U[M∩(∁UP)]}=M∩{(∁UM)∪ [∁U(∁UP)]}=M∩[(∁UM)∪P]=[M∩(∁UM)]∪(M∩P)=⌀∪(M∩P)=M∩P.(如图) 答案:M∩P 9.设 U=R,已知集合 A={x|-5<x<5},B={x|0≤x<7}, 求:(1)A∩B;(2)A∪B;(3)A∪(∁UB); (4)B∩(∁UA);(5)(∁UA)∩(∁UB). 解:如图①. (1)A∩B={x|0≤x<5}. (2)A∪B={x|-5<x<7}. 图① 图② (3)如图②. ∁UB={x|x<0 或 x≥7}, ∴A∪(∁UB)={x|x<5 或 x≥7}. (4)如图③

CuA 图③ CA={xr≤-5或x≥5},Bn(CuA)={x5≤x1; 2a-3≤-a, 当C≠o时,则2a-3>2,解得a∈o. -a<5, 综上,a的取值范围为(1,+oo), 拓展提高 1.已知全集U(U≠a),子集M,N,P,且M=CN,N=CP,则M与P的关系是() A.M=CuP B.M=P C.M厍P D.PSM 解析:P=C(CuP)=CN=M 答案B 2.若全集U={1,2,3,4,5,6},M={2,3},N={1,4},则集合{5,6}等于() A.MUN B.MON C.(CUM)U(CUN)D.(CUMn(CUN) 解析::全集U={1,2,3,4,5,6},M={2,3},N={1,4}, .MUN={1,2,3,4} ..(CUM)n(CUN)=CU(MUN)=(5,6). 故选D 答案D 3.己知全集U={1,2,3,4,5},集合A={xx2-3x+2=0},B={xx=2a,a∈A},则集合C(AU B)中的元素个数为()
图③ ∁UA={x|x≤-5 或 x≥5},B∩(∁UA)={x|5≤x1; 当 C≠⌀时,则{ 2𝑎-3 ≤ -𝑎, 2𝑎-3 > 2, -𝑎 < 5, 解得 a∈⌀. 综上,a 的取值范围为(1,+∞). 拓展提高 1.已知全集 U(U≠⌀),子集 M,N,P,且 M=∁UN,N=∁UP,则 M 与 P 的关系是( ) A.M=∁UP B.M=P C.M⫋P D.P⫋M 解析:P=∁U(∁UP)=∁UN=M. 答案:B 2.若全集 U={1,2,3,4,5,6},M={2,3},N={1,4},则集合{5,6}等于( ) A.M∪N B.M∩N C.(∁UM)∪(∁UN) D.(∁UM)∩(∁UN) 解析:∵全集 U={1,2,3,4,5,6},M={2,3},N={1,4}, ∴M∪N={1,2,3,4}, ∴(∁UM)∩(∁UN)=∁U(M∪N)={5,6}. 故选 D. 答案:D 3.已知全集 U={1,2,3,4,5},集合 A={x|x2 -3x+2=0},B={x|x=2a,a∈A},则集合∁U(A∪ B)中的元素个数为( )
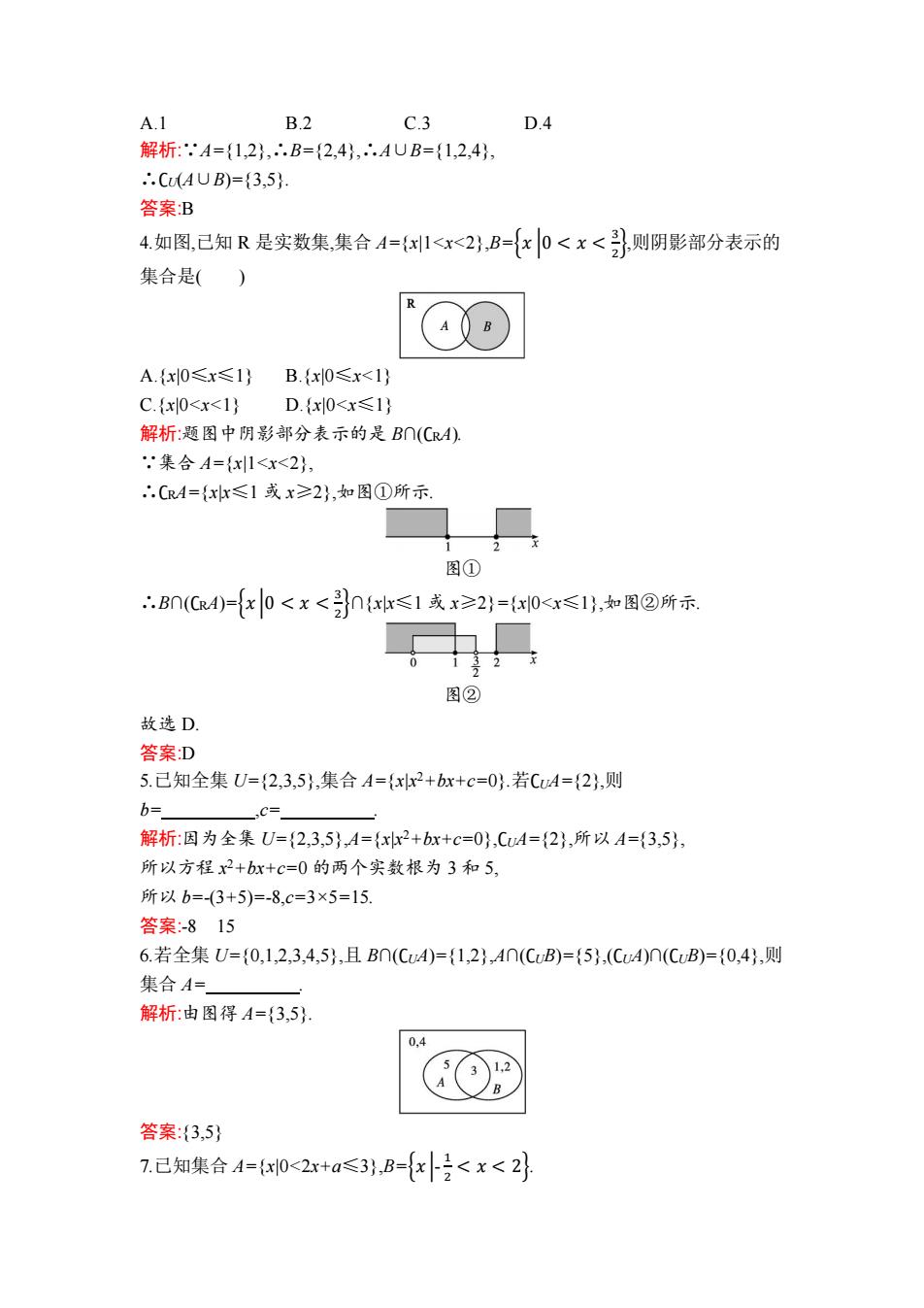
A.1 B.2 C.3 D.4 解析:A={1,2},.B={2,4},∴.AUB={1,2,4}, .CAUB)={3,5} 答案B 4.如图,已知R是实数集,集合A={1<<2},B={x|0<x<引}则阴影部分表示的 集合是() A.{x0≤x≤1}B.{x0≤x<1} C.{x0<x<1} D.{x|0<x≤1} 解析:题图中阴影部分表示的是B∩(CRA) 集合A={x1<x<2}, ∴.CRA={xx≤1或x≥2},如图①所示 图① ∴Bn(C4)={x]0<x<}nx≤1或x≥2}={x0<x≤1},知图②所示 图② 故选D. 答案D 5.己知全集U={2,3,5},集合A={xr2+bx+c=0}.若CA={2,则 b= ,C= 解析:因为全集U={2,3,5},A={xx2+bx+c=0},C4={2},所以A={3,5}, 所以方程x2+bx+C=0的两个实数根为3和5, 所以b=-(3+5)=-8,c=3×5=15 答案:-815 6.若全集U={0,1,2,3,4,5},且Bn(CA)={1,2},A∩(CB)={5},(C4A)n(CuB)={0,4},则 集合A= 解析:由图得A={3,5} 0,4 答案:{3,5} 7.已知集合A={x0<2x+a≤3},B={x2<x<2}
A.1 B.2 C.3 D.4 解析:∵A={1,2},∴B={2,4},∴A∪B={1,2,4}, ∴∁U(A∪B)={3,5}. 答案:B 4.如图,已知 R 是实数集,集合 A={x|1<x<2},B={𝑥 |0 < 𝑥 < 3 2 },则阴影部分表示的 集合是( ) A.{x|0≤x≤1} B.{x|0≤x<1} C.{x|0<x<1} D.{x|0<x≤1} 解析:题图中阴影部分表示的是 B∩(∁RA). ∵集合 A={x|1<x<2}, ∴∁RA={x|x≤1 或 x≥2},如图①所示. 图① ∴B∩(∁RA)={𝑥 |0 < 𝑥 < 3 2 }∩{x|x≤1 或 x≥2}={x|0<x≤1},如图②所示. 图② 故选 D. 答案:D 5.已知全集 U={2,3,5},集合 A={x|x2+bx+c=0}.若∁UA={2},则 b= ,c= . 解析:因为全集 U={2,3,5},A={x|x2+bx+c=0},∁UA={2},所以 A={3,5}, 所以方程 x 2+bx+c=0 的两个实数根为 3 和 5, 所以 b=-(3+5)=-8,c=3×5=15. 答案:-8 15 6.若全集 U={0,1,2,3,4,5},且 B∩(∁UA)={1,2},A∩(∁UB)={5},(∁UA)∩(∁UB)={0,4},则 集合 A= . 解析:由图得 A={3,5}. 答案:{3,5} 7.已知集合 A={x|0<2x+a≤3},B={𝑥 |- 1 2 < 𝑥 < 2}

(I)当a=1时,求(CRB)UA; (2)若A∩B=A,求实数a的取值范围 解(0当a=1时4=0<2x+1≤3)-x≤1 :B=x<x<2, ∴CB={xk≤或x≥2 ∴.(CRB)UA={xx≤1或x≥2} (2)若A∩B=A,则A二B. :4=x0<2x+a≤3)=<x≤受, :信≥解得1a≤L 3-0<2, .实数a的取值范围是{a-1<a≤I} 挑战创新 设集合A={x2x2+ax+2=0},B={xx2+3x+2a=0},A∩B={2. (I)求a的值及集合A,B: (2)设全集I=AUB,求(CA)U(CB): (3)写出(C4)U(CB)的所有子集 解1)国为AnB={2,所以2×22+2a+2=0,解得a=-5,所以A=位2},B={-5,2}. 2)国为I={5,2},所以CA={-5},CB=得所以(CAU(CB)={5,引 (3CAU(CB)的所有子集为@,{-5},{5,引
(1)当 a=1 时,求(∁RB)∪A; (2)若 A∩B=A,求实数 a 的取值范围. 解:(1)当 a=1 时,A={x|0<2x+1≤3}= x|- 1 2 <x≤1 . ∵B={𝑥 |- 1 2 < 𝑥 < 2}, ∴∁RB={𝑥 |𝑥 ≤ - 1 2 或𝑥 ≥ 2}. ∴(∁RB)∪A={x|x≤1 或 x≥2}. (2)若 A∩B=A,则 A⊆B. ∵A={x|0<2x+a≤3}= x|- 𝑎 2 < 𝑥 ≤ 3-𝑎 2 , ∴{ - 𝑎 2 ≥ - 1 2 , 3-𝑎 2 < 2, 解得-1<a≤1, ∴实数 a 的取值范围是{a|-1<a≤1}. 挑战创新 设集合 A={x|2x 2+ax+2=0},B={x|x2+3x+2a=0},A∩B={2}. (1)求 a 的值及集合 A,B; (2)设全集 I=A∪B,求(∁IA)∪(∁IB); (3)写出(∁IA)∪(∁IB)的所有子集. 解:(1)因为 A∩B={2},所以 2×2 2+2a+2=0,解得 a=-5,所以 A={ 1 2 ,2},B={-5,2}. (2)因为 I={-5, 1 2 ,2},所以∁IA={-5},∁IB={ 1 2 },所以(∁IA)∪(∁IB)={-5, 1 2 }. (3)(∁IA)∪(∁IB)的所有子集为⌀,{ 1 2 },{-5},{-5, 1 2 }