
第2课时 函数的最大(小)值 课后·图象 基础巩固 1,x>0 1.函数x)=0,x=0,的最大值和最小值分别是( -1,x<0 A.0,-1 B.1,-1 C.1,0 D.没有最大值和最小值 解析:函数x)的函数值只有三个:1,0,-1, 所以函数x)的最大值为1,最小值为-1. 答案B 2.函数x)=1在区间2,81上的最小值与最大值分别为() A片 B31 D后时 解析:x)=二在区间[2,8]上单调递减, 当x=8时,xmm合 当x=2时rmx号 答案:A 3.函数gx)=x2-4x+3在区间(1,4]上的值域是() A.[-1,+o) B.[0,3] C.(-1,3] D.[-1,3] 解析:,gx)=(x-2)2-1, 当x=2时gx)min=-l 当x=4时g(x)max=3, g(x)在区间(1,4]上的值域为[-1,3] 答案D 4.函数x)=在区间[1,+o)内() A有最大值,无最小值 B.有最小值无最大值 C.有最大值,也有最小值 D.无最大值,也无最小值 解析:结合函数x)=二在区间[1,+0)内的图像可知,函数x)有最大值,无最小值
第 2 课时 函数的最大(小)值 课后· 基础巩固 1.函数 f(x)={ 1,𝑥 > 0, 0,𝑥 = 0, -1,𝑥 < 0 的最大值和最小值分别是( ) A.0,-1 B.1,-1 C.1,0 D.没有最大值和最小值 解析:函数 f(x)的函数值只有三个:1,0,-1, 所以函数 f(x)的最大值为 1,最小值为-1. 答案:B 2.函数 f(x)= 1 𝑥在区间[2,8]上的最小值与最大值分别为( ) A. 1 8 , 1 2 B. 1 3 ,1 C. 1 9 , 1 3 D. 1 8 , 1 3 解析:∵f(x)= 1 𝑥在区间[2,8]上单调递减, ∴当 x=8 时,f(x)min= 1 8 ; 当 x=2 时,f(x)max= 1 2 . 答案:A 3.函数 g(x)=x2 -4x+3 在区间(1,4]上的值域是( ) A.[-1,+∞) B.[0,3] C.(-1,3] D.[-1,3] 解析:∵g(x)=(x-2)2 -1, 当 x=2 时,g(x)min=-1; 当 x=4 时,g(x)max=3, ∴g(x)在区间(1,4]上的值域为[-1,3]. 答案:D 4.函数 f(x)= 1 𝑥在区间[1,+∞)内( ) A.有最大值,无最小值 B.有最小值,无最大值 C.有最大值,也有最小值 D.无最大值,也无最小值 解析:结合函数 f(x)= 1 𝑥在区间[1,+∞)内的图像可知,函数 f(x)有最大值,无最小值

答案:A 5.某公司在甲、乙两地同时销售一种品牌车,销售x辆该品牌车的利润(单位:万 元)分别为L1=-x2+21x和L2=2x.若该公司在两地共销售15辆,则能获得的最大利 润为() A.90万元 B.60万元 C.120万元 D.120.25万元 解析:设公司在甲地销售x辆,则在乙地销售(15-x)辆 公司获利为L=2421x+215-x)=-r2+19x+30=(x.)+30+1g 当x=9或10时,L最大为120万元 答案:C 6.若函数x)=x2+a在区间[1,4]上的最大值是18,则函数x)的最小值 是 解析:由题意知[1,4]是函数儿x)的递增区间, 所以4)=42+a=18,解得a=2 所以x)的最小值是1)=12+2=3. 答案:3 7.若函数y=ax+1(a>0)在区间[1,3]上的最大值为4,则a= 解析:,a>0,∴.函数y=ar+1在区间[1,3]上是增函数,max=3a+1=4,解得a=1. 答案:1 8.函数y= x+1x∈31的最小值为 最大值为 -x-1,x∈(-1,4] 解析:由题意可知,当x∈[-3,-1]时min=-2;当x∈(-1,4]时min=-5,故函数的最小值 为-5.同理可得,函数的最大值为0. 答案-50 x2-x,0≤x≤2, 9.己知函数x) x>2 求函数x)的最大值、最小值, 解:作出x)的图像如图,由图像可知,当x=2时x)取最大值为2;当x=1时,x)取最 小值为子 故x)的最大值为2,最小值为
答案:A 5.某公司在甲、乙两地同时销售一种品牌车,销售 x 辆该品牌车的利润(单位:万 元)分别为 L1=-x 2+21x 和 L2=2x.若该公司在两地共销售 15 辆,则能获得的最大利 润为( ) A.90 万元 B.60 万元 C.120 万元 D.120.25 万元 解析:设公司在甲地销售 x 辆,则在乙地销售(15-x)辆, 公司获利为 L=-x 2+21x+2(15-x)=-x 2+19x+30=-(𝑥- 19 2 ) 2 +30+ 19 2 4 , 当 x=9 或 10 时,L 最大为 120 万元. 答案:C 6.若函数 f(x)=x2+a 在区间[1,4]上的最大值是 18,则函数 f(x)的最小值 是 . 解析:由题意知[1,4]是函数 f(x)的递增区间, 所以 f(4)=4 2+a=18,解得 a=2, 所以 f(x)的最小值是 f(1)=1 2+2=3. 答案:3 7.若函数 y=ax+1(a>0)在区间[1,3]上的最大值为 4,则 a= . 解析:∵a>0,∴函数 y=ax+1 在区间[1,3]上是增函数,∴ymax=3a+1=4,解得 a=1. 答案:1 8.函数 y={ 𝑥 + 1,𝑥∈[-3,-1], -𝑥-1,𝑥∈(-1,4] 的最小值为 ,最大值为 . 解析:由题意可知,当 x∈[-3,-1]时,ymin=-2;当 x∈(-1,4]时,ymin=-5,故函数的最小值 为-5.同理可得,函数的最大值为 0. 答案:-5 0 9.已知函数 f(x)={ 𝑥 2 -𝑥,0 ≤ 𝑥 ≤ 2, 2 𝑥-1 ,𝑥 > 2, 求函数 f(x)的最大值、最小值. 解:作出 f(x)的图像如图,由图像可知,当 x=2 时,f(x)取最大值为 2;当 x= 1 2时,f(x)取最 小值为- 1 4 . 故 f(x)的最大值为 2,最小值为- 1 4

10已知函数x∈B,5 (1)判断函数x)的单调性,并给出证明; (2)求函数x)的最大值和最小值 解(1)x)在区间[3,5]上是增函数 证明如下:任取x1,2∈[3,5],且x10 ∴x1)x2)0,即x1)x2) x)在区间[3,5上为增函数 (2)由(1)知,x)在区间[3,5]上为增函数, 则xhmx=5)=x)min=3)=号 拓展提高 1.若当0≤x≤2时,a<-x2+2x恒成立,则实数a的取值范围是( A.(-0,1] B.(-0,0] C.(-0,0) D.(0,+0 解析:令x)=-x2+2x 则x)=-x2+2x=-(x-1)2+1 .∴x∈[0,2],∴.xmim=f0)=2)=0. ∴.a<0. 答案:C 2.己知函数x)=4x2-x-8在区间(5,20)内既没有最大值也没有最小值,则实数k的 取值范围是( A.[160,+∞) B.(-0,40] C.(-0,40]U[160,+o) D.(-o0,20]U[80,+o) 解析:由于二次函数x)=4x2-x-8在区间(5,20)内既没有最大值也没有最小值,因 此函数x)=4x2-x-8在区间(5,20)内是单调函数.由于二次函数x)=4x2-r-8图像 的对称轴方程为x=因此≤5或≥20,解得≤40或k≥160. 答案:C 3.函数y=x+√2x-1的最值的情况为( A.最小值为,无最大值 B最大值为无最小值 C.最小值为号最大值为2 D.最大值为2,无最小值
10.已知函数 f(x)= 𝑥-1 𝑥+2 ,x∈[3,5]. (1)判断函数 f(x)的单调性,并给出证明; (2)求函数 f(x)的最大值和最小值. 解:(1)f(x)在区间[3,5]上是增函数. 证明如下:任取 x1,x2∈[3,5],且 x10, ∴f(x1)-f(x2)<0,即 f(x1)<f(x2), ∴f(x)在区间[3,5]上为增函数. (2)由(1)知,f(x)在区间[3,5]上为增函数, 则 f(x)max=f(5)= 4 7 ,f(x)min=f(3)= 2 5 . 拓展提高 1.若当 0≤x≤2 时,a<-x 2+2x 恒成立,则实数 a 的取值范围是( ) A.(-∞,1] B.(-∞,0] C.(-∞,0) D.(0,+∞) 解析:令 f(x)=-x 2+2x, 则 f(x)=-x 2+2x=-(x-1)2+1. ∵x∈[0,2],∴f(x)min=f(0)=f(2)=0. ∴a<0. 答案:C 2.已知函数 f(x)=4x 2 -kx-8 在区间(5,20)内既没有最大值也没有最小值,则实数 k 的 取值范围是( ) A.[160,+∞) B.(-∞,40] C.(-∞,40]∪[160,+∞) D.(-∞,20]∪[80,+∞) 解析:由于二次函数 f(x)=4x 2 -kx-8 在区间(5,20)内既没有最大值也没有最小值,因 此函数 f(x)=4x 2 -kx-8 在区间(5,20)内是单调函数.由于二次函数 f(x)=4x 2 -kx-8 图像 的对称轴方程为 x= 𝑘 8 ,因此𝑘 8 ≤5 或 𝑘 8 ≥20,解得 k≤40 或 k≥160. 答案:C 3.函数 y=x+√2𝑥-1的最值的情况为( ) A.最小值为1 2 ,无最大值 B.最大值为1 2 ,无最小值 C.最小值为1 2 ,最大值为 2 D.最大值为 2,无最小值

解析:“y=x+V2x在定义城位+∞内是增函数,函数的最小值为无最大值, 故选A. 答案:A 4.下列函数:①y=x+x②y=x-x③y=xx;④y=其中有最小值的函数有」 个 0,x0, y=xx|= -x2,x≤0, 无最小值 1,x>0, y=1x<0场ms月 答案2 5如图,在锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴影部分),其一 边长为x,则x= m 40m 解析:设矩形花园的另一边长为y,则名=0贮,即y=40x,矩形花园的面积S=x(40 40 40 x)=-x2+40x=-(x-20)2+400,当x=20m时,S最大 答案20 6.己知函数x)=x2-6x+8,x∈[1,ad,且x)的最小值为a),则实数a的取值范围 是 解析:如图可知x)在区间[1,a上单调递减 又x)的单调递减区间为(0,3] .1<a≤3 答案:(1,3] 7.某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需要增加投 入100元,最大月产量是400台.已知总收益满足函数Rx)=400xx2,其中x是仪 器的月产量(单位:台) (1)将利润单位:元)表示为月产量x(单位:台)的函数;
解析:∵y=x+√2𝑥-1在定义域[ 1 2 , + ∞)内是增函数,∴函数的最小值为1 2 ,无最大值, 故选 A. 答案:A 4.下列函数:①y=x+|x|;②y=x-|x|;③y=x|x|;④y= 𝑥 |𝑥| .其中有最小值的函数有 个. 解析:y=x+|x|={ 0,𝑥 0, 2𝑥,𝑥 ≤ 0, 无最小值; y=x|x|={ 𝑥 2 ,𝑥 > 0, -𝑥 2 ,𝑥 ≤ 0, 无最小值; y= 𝑥 |𝑥| = { 1,𝑥 > 0, -1,𝑥 < 0, ymin=-1. 答案:2 5.如图,在锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴影部分),其一 边长为 x,则 x= m. 解析:设矩形花园的另一边长为 y,则 𝑥 40 = 40-𝑦 40 ,即 y=40-x,矩形花园的面积 S=x(40- x)=-x 2+40x=-(x-20)2+400,当 x=20 m 时,S 最大. 答案:20 6.已知函数 f(x)=x2 -6x+8,x∈[1,a],且 f(x)的最小值为 f(a),则实数 a 的取值范围 是 . 解析:如图可知 f(x)在区间[1,a]上单调递减. 又∵f(x)的单调递减区间为(-∞,3], ∴1<a≤3. 答案:(1,3] 7.某公司生产一种电子仪器的固定成本为 20 000 元,每生产一台仪器需要增加投 入 100 元,最大月产量是 400 台.已知总收益满足函数 R(x)=400x- 1 2 x 2 ,其中 x 是仪 器的月产量(单位:台). (1)将利润 y(单位:元)表示为月产量 x(单位:台)的函数;
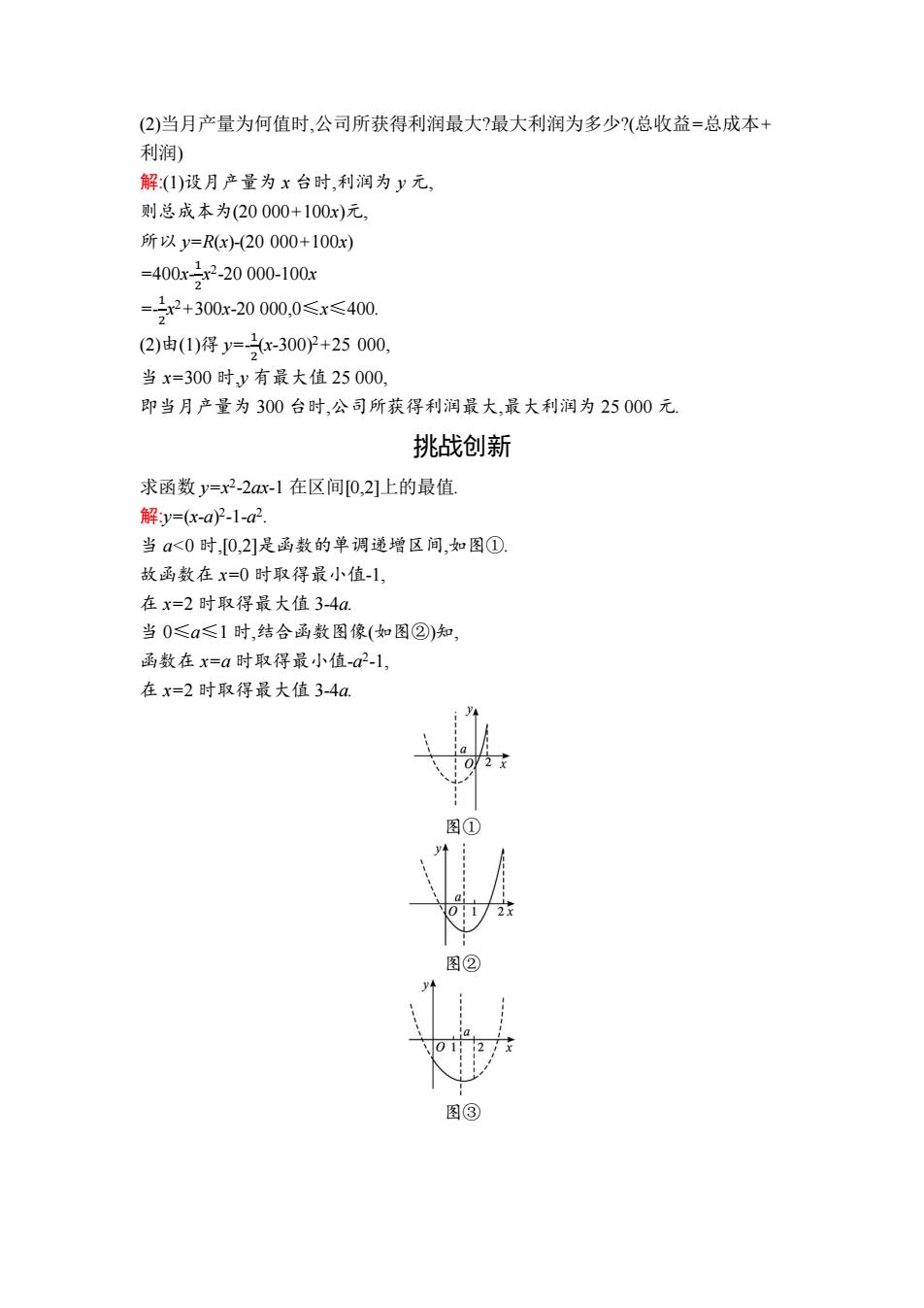
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少?(总收益=总成本+ 利润) 解(1)设月产量为x台时,利润为y元, 则总成本为(20000+100x)元, 所以y=R(x)-(20000+100x) =400x2x2-20000-100x =22+300x-2000,0≤x≤40, 2)由(1)得y=-300P+25000, 当x=300时y有最大值25000 即当月产量为300台时,公司所获得利润最大,最大利润为25000元 挑战创新 求函数y=x2-2ax-1在区间[0,2]上的最值. 解y=(x-a2-1-a2 当a<0时,[0,2]是函数的单调递增区间,如图①. 故函数在x=0时取得最小值-1, 在x=2时取得最大值3-4a. 当0≤a≤1时,结合函数图像(如图②)知, 函数在x=a时取得最小值-2-1, 在x=2时取得最大值3-4a. 图① 图② 图③
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少?(总收益=总成本+ 利润) 解:(1)设月产量为 x 台时,利润为 y 元, 则总成本为(20 000+100x)元, 所以 y=R(x)-(20 000+100x) =400x- 1 2 x 2 -20 000-100x =- 1 2 x 2+300x-20 000,0≤x≤400. (2)由(1)得 y=- 1 2 (x-300)2+25 000, 当 x=300 时,y 有最大值 25 000, 即当月产量为 300 台时,公司所获得利润最大,最大利润为 25 000 元. 挑战创新 求函数 y=x2 -2ax-1 在区间[0,2]上的最值. 解:y=(x-a) 2 -1-a 2 . 当 a<0 时,[0,2]是函数的单调递增区间,如图①. 故函数在 x=0 时取得最小值-1, 在 x=2 时取得最大值 3-4a. 当 0≤a≤1 时,结合函数图像(如图②)知, 函数在 x=a 时取得最小值-a 2 -1, 在 x=2 时取得最大值 3-4a. 图① 图② 图③

图④ 当12时,[0,2]是函数的单调递减区间,如图④. 函数在x=0时取得最大值-1, 在x=2时取得最小值3-4a
图④ 当 12 时,[0,2]是函数的单调递减区间,如图④. 函数在 x=0 时取得最大值-1, 在 x=2 时取得最小值 3-4a