
第4课时分段函数及其应用 课后·训练提升 基础巩固 1已知函数-+2女4共中侧装不不超过m的设大整数则从甲地到乙 地通话5.2min的话费是() A.3.71元 B.4.24元 C.4.77元 D.7.95元 解析:5.2)=1.06×(0.5×[5.2]+2)=1.06×(2.5+2)=4.77(元) 答案:C
第 4 课时 分段函数及其应用 课后· 基础巩固 1.已知函数 f(x)={ 𝑥-5,𝑥 ≥ 6, 𝑓(𝑥 + 2),𝑥 4, 其中[m]表示不超过 m 的最大整数,则从甲地到乙 地通话 5.2 min 的话费是( ) A.3.71 元 B.4.24 元 C.4.77 元 D.7.95 元 解析:f(5.2)=1.06×(0.5×[5.2]+2)=1.06×(2.5+2)=4.77(元). 答案:C
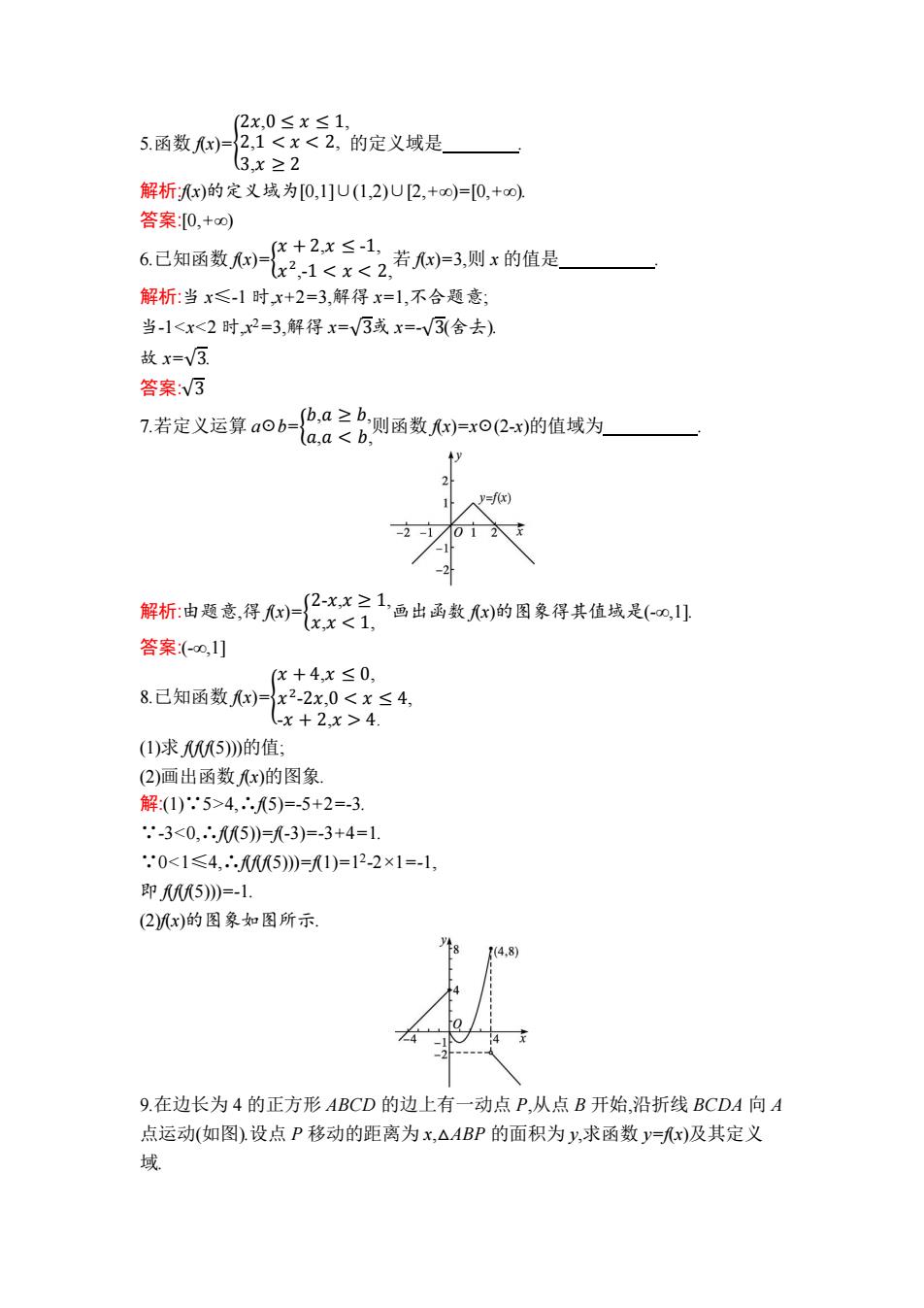
2x,0≤x≤1, 5.函数x)= 2,14. (1)求5))的值: (2)画出函数x)的图象 解(1).5>4,∴5)=-5+2=-3. -3<0,5)=-3)=-3+4=1. .0<1≤4,.5)》=1)=12-2×1=-1 即5))=-1. (2)(x)的图象如图所示. 8) 9.在边长为4的正方形ABCD的边上有一动点P,从点B开始,沿折线BCDA向A 点运动(如图).设点P移动的距离为x,△ABP的面积为y,求函数y=x)及其定义 域
5.函数 f(x)={ 2𝑥,0 ≤ 𝑥 ≤ 1, 2,1 4. (1)求 f(f(f(5)))的值; (2)画出函数 f(x)的图象. 解:(1)∵5>4,∴f(5)=-5+2=-3. ∵-3<0,∴f(f(5))=f(-3)=-3+4=1. ∵0<1≤4,∴f(f(f(5)))=f(1)=1 2 -2×1=-1, 即 f(f(f(5)))=-1. (2)f(x)的图象如图所示. 9.在边长为 4 的正方形 ABCD 的边上有一动点 P,从点 B 开始,沿折线 BCDA 向 A 点运动(如图).设点 P 移动的距离为 x,△ABP 的面积为 y,求函数 y=f(x)及其定义 域

解:如图,当点P在线段BC上,即0≤x≤4时y=之×4x=2x 当点P在线段CD上,即40 1.设x∈R定义符号函数sgnx=0,x=0,则( -1,x0,则a+1>1. a)=a+1), ∴√a=2(a+1-1), 解得a=∴(得)4)=2×4-1)=6,故选C 答案:C 3.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过103 的,按每立方米m元收费:用水超过10m3的,超过部分按每立方米2m元收费.某 职工某月缴水费16m元,则该职工这个月实际用水为() A.13m3 B.14m3 C.18m3 D.26m3
解:如图,当点 P 在线段 BC 上,即 0≤x≤4 时,y= 1 2 ×4x=2x; 当点 P 在线段 CD 上,即 4 0, 0,𝑥 = 0, -1,𝑥 0,则 a+1>1. ∵f(a)=f(a+1), ∴√𝑎=2(a+1-1), 解得 a= 1 4 ,∴f( 1 𝑎 )=f(4)=2×(4-1)=6,故选 C. 答案:C 3.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过 10 m3 的,按每立方米 m 元收费;用水超过 10 m3 的,超过部分按每立方米 2m 元收费.某 职工某月缴水费 16m 元,则该职工这个月实际用水为( ) A.13 m3 B.14 m3 C.18 m3 D.26 m3

解析:该单位职工每月应缴水费y与实际用水量x满足的关系式为 -6010 由y=16m,可知x>10. 令2mx-10m=16m,解得x=13(m3). 答案A 4.如图,函数图象是由两条射线及抛物线的一部分组成,则该函数的解析式 为 解析:当x≤1时,设x)=x+b,由0)=b=21)=k+b=1,得b=2,k=-1,即x)=x+2; 同理可得当x≥3时,x)=x-2,当1≤x≤3时,设x)=a(x-2}+2,a<0,又1)=a(1- 22+2=1,解得a=-1, 则x)=-(x-2)2+2=-x2+4x-2 (-x+2,x≤1, 所以x)=-x2+4x-2,1<x<3, x-2,x≥3. -x+2,x≤1 答案y=} -x2+4x-2,1<x<3, x-2,x≥3 5已知)=之0则不等式+x≤2的解集是 0,x<0, 解析:当x≥0时x)=1,代入xx)+x≤2,解得x≤1,即0≤x≤1;当x<0时x)=0,代 入x)+x≤2,解得x≤2,即x<0.综上可知x≤1. 答案:{xk≤I} 6分段丽数和-三0可以表示为分段商数仔经三务可表示为 x)=x+3-x-3)仿照上述式子,分段函数x) 6,x<6可表示为 (x,x≥6 x)= 解析:国为仔可表示为+3-3儿共分界点为3,从而式子中含 有x+3与x-3,并通过x-3引前面的“构造出需要的结果的形式.所以,对于分段函数 8共分界点为6数式子中痘合有x46与x6又当x6时=6故 6的前面应取“+”.因此x)=x+6+r-6) 答案x+6+x-6) 7.为鼓励节约用水,某市打算出台一项水费政策措施,规定:每季度每人用水量不超 过5t时,每吨水费收基本价1.3元;若超过5t而不超过6t,则超过部分水费加收
解析:该单位职工每月应缴水费 y 与实际用水量 x 满足的关系式为 y={ 𝑚𝑥,0 ≤ 𝑥 ≤ 10, 2𝑚𝑥-10𝑚,𝑥 > 10. 由 y=16m,可知 x>10. 令 2mx-10m=16m,解得 x=13(m3 ). 答案:A 4.如图,函数图象是由两条射线及抛物线的一部分组成,则该函数的解析式 为 . 解析:当 x≤1 时,设 f(x)=kx+b,由 f(0)=b=2,f(1)=k+b=1,得 b=2,k=-1,即 f(x)=-x+2; 同理可得当 x≥3 时,f(x)=x-2;当 1≤x≤3 时,设 f(x)=a(x-2)2+2,a 0, -𝑥,𝑥 ≤ 0 可以表示为 f(x)=|x|,分段函数 f(x)={ 𝑥,𝑥 ≤ 3, 3,𝑥 > 3 可表示为 f(x)= 1 2 (x+3-|x-3|).仿照上述式子,分段函数 f(x)={ 6,𝑥 3 可表示为 f(x)= 1 2 (x+3-|x-3|),其分界点为 3,从而式子中含 有 x+3 与 x-3,并通过|x-3|前面的“-”构造出需要的结果的形式.所以,对于分段函数 f(x)={ 6,𝑥 < 6, 𝑥,𝑥 ≥ 6, 其分界点为 6,故式子中应含有 x+6 与 x-6.又当 x<6 时,f(x)=6,故|x- 6|的前面应取“+”.因此 f(x)= 1 2 (x+6+|x-6|). 答案: 1 2 (x+6+|x-6|) 7.为鼓励节约用水,某市打算出台一项水费政策措施,规定:每季度每人用水量不超 过 5 t 时,每吨水费收基本价 1.3 元;若超过 5 t 而不超过 6 t,则超过部分水费加收

200%:若超过6t而不超过7t时,超过部分的水费加收400%.如果某人本季度实 际用水量为xtx≤7),试计算,本季度他应交多少水费? 解:用y表示本季度应交水费(单位:元)】 当00: (3)若直线y=a与x)的图象无交点,求实数a的取值范围. 解:若x≤-1,则x-30, x)=-(x-3)(x+1)=-2x+2; 若x>3,则x-3>0x+1>0 x)=(x-3)H(x+1)=-4 4,x≤-1, 故x)= -2x+2,-13. (1)当-10的解集为(-0,-1]U(-1,1)U⑦=(-0,1)】 (3)x)的图象如下:
200%;若超过 6 t 而不超过 7 t 时,超过部分的水费加收 400%.如果某人本季度实 际用水量为 x t(x≤7),试计算,本季度他应交多少水费? 解:用 y 表示本季度应交水费(单位:元). 当 00; (3)若直线 y=a 与 f(x)的图象无交点,求实数 a 的取值范围. 解:若 x≤-1,则 x-30, f(x)=-(x-3)-(x+1)=-2x+2; 若 x>3,则 x-3>0,x+1>0, f(x)=(x-3)-(x+1)=-4. 故 f(x)={ 4,𝑥 ≤ -1, -2𝑥 + 2,-1 3. (1)当-10,即{ 𝑥 ≤ -1, 4 > 0 ① 或{ -1 0 ② 或{ 𝑥 > 3, -4 > 0, ③ 解①得 x≤-1,解②得-10 的解集为(-∞,-1]∪(-1,1)∪⌀=(-∞,1). (3)f(x)的图象如下:

4-2024x -21 由图可知,当a∈(-o,-4)U(4,+oo)时,直线y=a与x)的图象无交点
由图可知,当 a∈(-∞,-4)∪(4,+∞)时,直线 y=a 与 f(x)的图象无交点