
第八章成对数据的统计分析 8.1成对数据的统计相关性 课后训练提升 基础巩固 1判断下图中的两个变量,具有较强相关关系的是( 答案B 解析:A,C是函数关系,D中的散点杂乱无章,无规律可言,看不出两个变量有什么 相关性 2.在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并 制作成散点图如图所示,根据该图,下列结论中正确的是() ↑脂肪含量(%) 35 30 25 20 15 10 5 1015202530354045505560年龄 A.人体脂肪含量与年龄正相关,且脂肪含量的中位数等于20% B.人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20% C.人体脂肪含量与年龄负相关,且脂肪含量的中位数等于20% D.人体脂肪含量与年龄负相关,且脂肪含量的中位数小于20% 答案B 解析:由散点图可知点的分布都集中在一条直线附近,由此可以判断两个变量具有 相关关系,点的分布从左下角到右上角区城,因此是正相关.由散点图可知共有10 个点,则中位数为最中间两点的纵坐标的平均数,因为两数均小于20%,所以脂肪 含量的中位数小于20% 3.(多选题)下列说法错误的是( A相关关系是函数关系 B.函数关系是相关关系 C.线性相关关系是一次函数关系 D.相关关系有两种,分别是线性相关关系和非线性相关关系
第八章 成对数据的统计分析 8.1 成对数据的统计相关性 课后· 基础巩固 1.判断下图中的两个变量,具有较强相关关系的是( ) 答案:B 解析:A,C 是函数关系,D 中的散点杂乱无章,无规律可言,看不出两个变量有什么 相关性. 2.在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并 制作成散点图如图所示,根据该图,下列结论中正确的是( ) A.人体脂肪含量与年龄正相关,且脂肪含量的中位数等于 20% B.人体脂肪含量与年龄正相关,且脂肪含量的中位数小于 20% C.人体脂肪含量与年龄负相关,且脂肪含量的中位数等于 20% D.人体脂肪含量与年龄负相关,且脂肪含量的中位数小于 20% 答案:B 解析:由散点图可知点的分布都集中在一条直线附近,由此可以判断两个变量具有 相关关系,点的分布从左下角到右上角区城,因此是正相关.由散点图可知共有 10 个点,则中位数为最中间两点的纵坐标的平均数,因为两数均小于 20%,所以脂肪 含量的中位数小于 20%. 3.(多选题)下列说法错误的是( ) A.相关关系是函数关系 B.函数关系是相关关系 C.线性相关关系是一次函数关系 D.相关关系有两种,分别是线性相关关系和非线性相关关系

答案:ABC 解析:函数关系和相关关系互不包含,A,B,C三项不正确:根据定义,相关关系有两 种,分别是线性相关关系和非线性相关关系D选项正确 4.己知xy是两个变量,下列四个散点图中,x,y呈负相关趋势的是() y 232 012345x A B 0012345 012345x C D 答案C 解析:对于A,散,点图中的点从左向右是上升的,且分布在一条直线附近,是正相关 关系; 对于B,散点图中的点不成带状分布,没有明显的相关关系; 对于C,散,点图中的点从左向右是下降的,且在一条直线附近,是负相关关系: 对于D,散点图中的,点不成带状分布,没有明显的相关关系 5.(多选题)对两个变量的样本相关系数r,下列说法错误的是() A.越大,成对样本数据的相关程度越强 B.越小,成对样本数据的相关程度越强 C.r趋近于0时,没有非线性相关系数 D.越接近于1时,成对样本数据的线性相关程度越弱 答案BCD 解析:对于A,越大,成对样本数据的相关程度越强,正确; 对于B,越小,成对样本数据的相关程度越弱,错误; 对于C,趋近于0时,成对样本数据的线性相关程度较弱,错误; 对于D,r越接近于1时,成对样本数据的线性相关程度越强,错误 6.下面各组变量之间具有线性相关关系的是 (填序号) ①高原含氧量与海拔高度, ②速度一定时,汽车行驶的路程和所用的时间; ③学生的成绩和学生的学号 答案:①
答案:ABC 解析:函数关系和相关关系互不包含,A,B,C 三项不正确;根据定义,相关关系有两 种,分别是线性相关关系和非线性相关关系.D 选项正确. 4.已知 x,y 是两个变量,下列四个散点图中,x,y 呈负相关趋势的是( ) 答案:C 解析:对于 A,散点图中的点从左向右是上升的,且分布在一条直线附近,是正相关 关系; 对于 B,散点图中的点不成带状分布,没有明显的相关关系; 对于 C,散点图中的点从左向右是下降的,且在一条直线附近,是负相关关系; 对于 D,散点图中的点不成带状分布,没有明显的相关关系. 5.(多选题)对两个变量的样本相关系数 r,下列说法错误的是( ) A.|r|越大,成对样本数据的相关程度越强 B.|r|越小,成对样本数据的相关程度越强 C.|r|趋近于 0 时,没有非线性相关系数 D.|r|越接近于 1 时,成对样本数据的线性相关程度越弱 答案:BCD 解析:对于 A,|r|越大,成对样本数据的相关程度越强,正确; 对于 B,|r|越小,成对样本数据的相关程度越弱,错误; 对于 C,|r|趋近于 0 时,成对样本数据的线性相关程度较弱,错误; 对于 D,|r|越接近于 1 时,成对样本数据的线性相关程度越强,错误. 6.下面各组变量之间具有线性相关关系的是 .(填序号) ①高原含氧量与海拔高度; ②速度一定时,汽车行驶的路程和所用的时间; ③学生的成绩和学生的学号. 答案:①

解析:由线性相关的定义可知①是线性相关关系」 7.有下列关系 ①人的年龄与他(她)拥有的财富之间的关系: ②学生与他(她)的学号之间的关系: ③森林中的同一种树木,其断面直径与高度之间的关系; ④曲线上的点与该点的坐标之间的关系 其中有相关关系的是 (填序号) 答案:①③ 解析:对于①,人的年龄与他(她)拥有的财富是一种不确定的相关关系;对于②,学 生与他(她)的学号之间的关系是一种确定的对应关系,不是相关关系;对于③,森林 中的同一种树木,其断面直径与高度之间的关系是一种不确定的关系,属于相关关 系;对于④,曲线上的点与该点的坐标之间的关系是一一对应关系,不是相关关系 综上,其中有相关关系的是①③ 8.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5)变量U 与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),n表示变量Y与X 之间的样本相关系数,”表示变量V与U之间的样本相关系数,则”1与n的大小 关系是 答案n0. 而由变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),可知 变量V与U之间负相关, 因此n<0. 故n与2的大小关系是n<n. 9.下面是水稻产量与施化肥量的一组观测数据 施化肥量 15 20 25 30 35 40 45 水稻产量 b20 330 360 410 460 470 480 (1)将上述数据制成散点图 (2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直 随施化肥量的增加而增长吗? 解(1)散,点图如图所示 水稻产量 500 400 300 200 100 1020304050→ 施化肥量
解析:由线性相关的定义可知①是线性相关关系. 7.有下列关系: ①人的年龄与他(她)拥有的财富之间的关系; ②学生与他(她)的学号之间的关系; ③森林中的同一种树木,其断面直径与高度之间的关系; ④曲线上的点与该点的坐标之间的关系. 其中有相关关系的是 .(填序号) 答案:①③ 解析:对于①,人的年龄与他(她)拥有的财富是一种不确定的相关关系;对于②,学 生与他(她)的学号之间的关系是一种确定的对应关系,不是相关关系;对于③,森林 中的同一种树木,其断面直径与高度之间的关系是一种不确定的关系,属于相关关 系;对于④,曲线上的点与该点的坐标之间的关系是一一对应关系,不是相关关系. 综上,其中有相关关系的是①③. 8.变量 X 与 Y 相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量 U 与 V 相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),r1 表示变量 Y 与 X 之间的样本相关系数,r2 表示变量 V 与 U 之间的样本相关系数,则 r1 与 r2 的大小 关系是 . 答案:r20. 而由变量 U 与 V 相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),可知 变量 V 与 U 之间负相关, 因此 r2<0. 故 r1 与 r2 的大小关系是 r2<r1. 9.下面是水稻产量与施化肥量的一组观测数据: 施化肥量 15 20 25 30 35 40 45 水稻产量 320 330 360 410 460 470 480 (1)将上述数据制成散点图; (2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直 随施化肥量的增加而增长吗? 解:(1)散点图如图所示:

(2)从图中发现数据点大致分布在一条直线附近,因此施化肥量和水稻产量近似成 线性相关关系,施化肥量由小到大时,水稻产量由小到大,但水稻产量不会一直随 施化肥量的增加而增长 拓展提高 1在一个数据组中,已知26ar是公0列的两倍,公c0r列是公0,卯的 1 1.2倍,试求这组数据的样本相关系数r(精确到0.001) 解r (- 设20r=a, i=1 则∑(x-x0r-)=1.2a, i=1 n (xr-x)2=2a. 故r0a=号0849, 2.某地10户家庭的年收入和年饮食支出的统计资料如表所示 年收入 10 万元 年饮食支 0.9 1.4 1.6 2.0 2.1 1.9 1.8 2. 2.3 出万元 根据表中数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相 关程度 解:先画出散点图,观察散点图,可以看出样本点都集中在一条直线的附近,由此可 以判断家庭的年收入和年饮食支出线性相关」 作散点图如图所示 2 012345678910元 根据样本相关系数的定义,可得 10 10 (x1-x(y1-) y-10元 ① 2y2102 11 1 10 10 10 国为元=65=183,名号=40627-=35.13,20=177, 代入①得
(2)从图中发现数据点大致分布在一条直线附近,因此施化肥量和水稻产量近似成 线性相关关系,施化肥量由小到大时,水稻产量由小到大,但水稻产量不会一直随 施化肥量的增加而增长. 拓展提高 1.在一个数据组中,已知 ∑ 𝑖=1 𝑛 (xi-x) 2 是 ∑ i=1 n (yi-𝑦) 2 的两倍, ∑ 𝑖=1 𝑛 (xi-𝑥)(yi-𝑦)是 ∑ 𝑖=1 𝑛 (yi-𝑦) 2 的 1.2 倍,试求这组数据的样本相关系数 r.(精确到 0.001) 解:r= ∑ 𝑖=1 𝑛 (xi -x)(yi -y) √ ∑ i=1 n (𝑥𝑖 -𝑥) 2√ ∑ 𝑖=1 𝑛 (𝑦𝑖 -𝑦) 2 , 设 ∑ 𝑖=1 𝑛 (yi-𝑦) 2=a, 则 ∑ 𝑖=1 𝑛 (xi-𝑥)(yi-𝑦)=1.2a, ∑ 𝑖=1 𝑛 (xi-𝑥) 2=2a, 故 r= 1.2𝑎 √2𝑎·√𝑎 = 1.2 √2 ≈0.849. 2.某地 10 户家庭的年收入和年饮食支出的统计资料如表所示. 年收入 x/万元 2 4 4 6 6 6 7 7 8 10 年饮食支 出 y/万元 0.9 1.4 1.6 2.0 2.1 1.9 1.8 2.1 2.2 2.3 根据表中数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相 关程度. 解:先画出散点图,观察散点图,可以看出样本点都集中在一条直线的附近,由此可 以判断家庭的年收入和年饮食支出线性相关. 作散点图如图所示. 根据样本相关系数的定义,可得 r= ∑ 𝑖=1 10 (xi -x)(yi -y) √ ∑ i=1 10 (𝑥𝑖 -𝑥) 2√ ∑ 𝑖=1 10 (𝑦𝑖 -𝑦) 2 = ∑ 𝑖=1 10 𝑥𝑖𝑦𝑖 -10𝑥 𝑦 √ ∑ 𝑖=1 10 𝑥𝑖 2 -10𝑥 2√ ∑ 𝑖=1 10 𝑦𝑖 2 -10𝑦 2 .① 因为𝑥=6,𝑦=1.83, ∑ 𝑖=1 10 𝑥𝑖 2=406, ∑ 𝑖=1 10 𝑦𝑖 2=35.13, ∑ 𝑖=1 10 xiyi=117.7, 代入①得
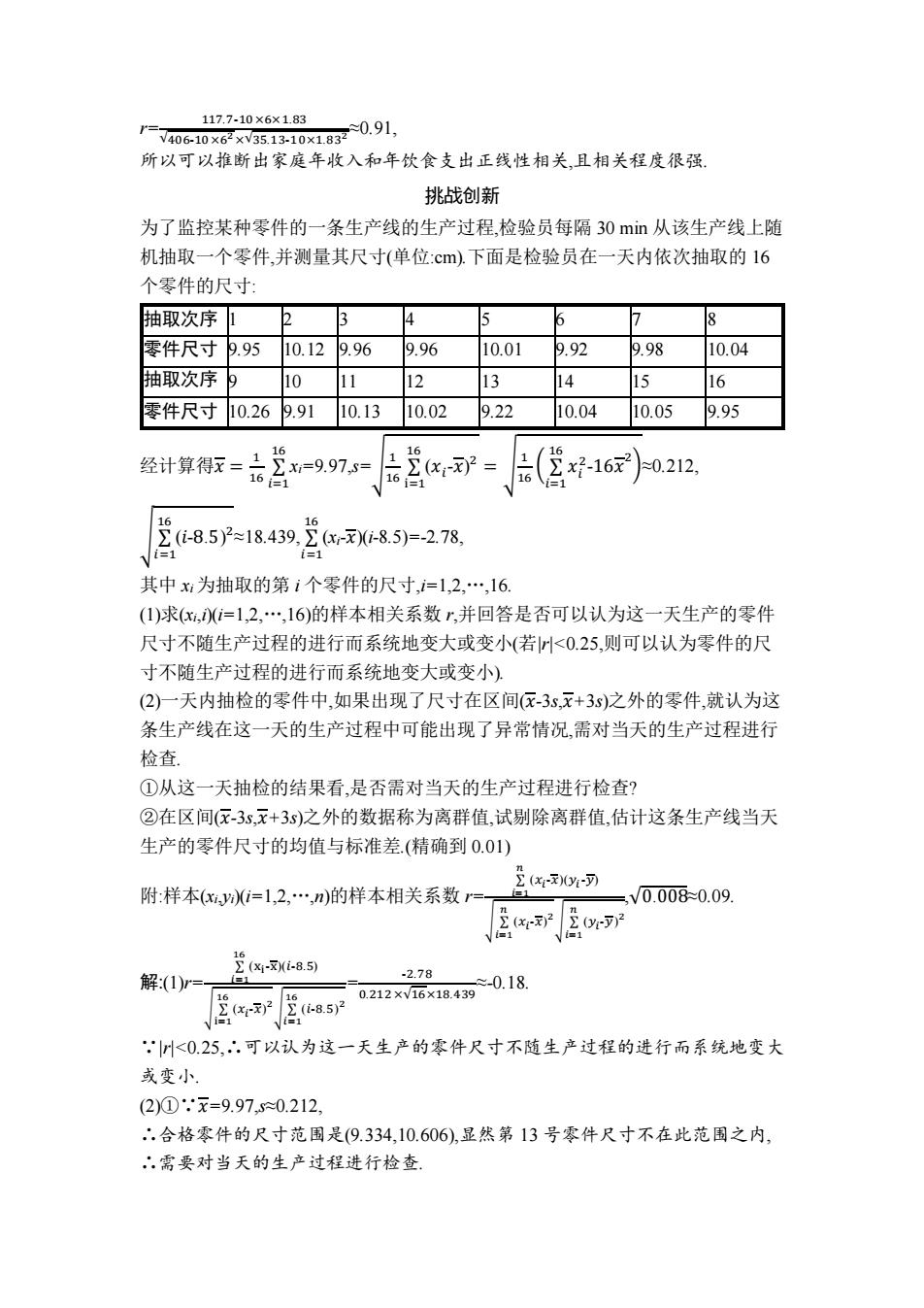
117.7-10×6×1.83 r7406-10x62x9513-10x1830.91, 所以可以推断出家庭年收入和年饮食支出正线性相关,且相关程度很强 挑战创新 为了监控某种零件的一条生产线的生产过程,检验员每隔30mi从该生产线上随 机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16 个零件的尺寸 抽取次序 2 3 8 零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04 抽取次序 10 11 12 13 14 15 16 零件尺寸 10.269.91 10.13 10.02 9.22 10.04 10.05 9.95 经计算得=六x-997, 2x=层(16022 16 16 (i-8.5)2≈18.439,Σ(rx)i-8.5)=-2.78 =1 =1 其中x为抽取的第i个零件的尺寸,i=1,2,…,16 (1)求(x,i=1,2,…,16)的样本相关系数r,并回答是否可以认为这一天生产的零件 尺寸不随生产过程的进行而系统地变大或变小(若<0.25,则可以认为零件的尺 寸不随生产过程的进行而系统地变大或变小)】 (2)一天内抽检的零件中,如果出现了尺寸在区间:-3s,x+3s)之外的零件,就认为这 条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行 检查 ①从这一天抽检的结果看,是否需对当天的生产过程进行检查? ②在区间(亿-3s,x+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天 生产的零件尺寸的均值与标准差.(精确到0.01) ∑(x-y1-列 附:样本(x,yi=1,2,…,n)的样本相关系数r √0.008≈0.09. (x- (y-)2 16 (x-x)(i-8.5) 解(1)r -2.78 ≈-0.18 16 0.212×√16×18.439 (t-8.5)2 川<0.25,.可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大 或变小 (2)①.x=9.970.212 ∴.合格零件的尺寸范围是(9.334,10.606),显然第13号零件尺寸不在此范围之内, .需要对当天的生产过程进行检查
r= 117.7-10 ×6×1.83 √406-10 ×6 2 ×√35.13-10×1.83 2 ≈0.91, 所以可以推断出家庭年收入和年饮食支出正线性相关,且相关程度很强. 挑战创新 为了监控某种零件的一条生产线的生产过程,检验员每隔 30 min 从该生产线上随 机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的 16 个零件的尺寸: 抽取次序 1 2 3 4 5 6 7 8 零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04 抽取次序 9 10 11 12 13 14 15 16 零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95 经计算得𝑥 = 1 16 ∑ 𝑖=1 16 xi=9.97,s=√ 1 16 ∑ i=1 16 (𝑥𝑖 -𝑥) 2 = √ 1 16 ( ∑ 𝑖=1 16 𝑥𝑖 2 -16𝑥 2 )≈0.212, √ ∑ 𝑖=1 16 (𝑖-8.5) 2 ≈18.439, ∑ 𝑖=1 16 (xi-𝑥)(i-8.5)=-2.78, 其中 xi 为抽取的第 i 个零件的尺寸,i=1,2,…,16. (1)求(xi,i)(i=1,2,…,16)的样本相关系数 r,并回答是否可以认为这一天生产的零件 尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺 寸不随生产过程的进行而系统地变大或变小). (2)一天内抽检的零件中,如果出现了尺寸在区间(𝑥-3s,𝑥+3s)之外的零件,就认为这 条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行 检查. ①从这一天抽检的结果看,是否需对当天的生产过程进行检查? ②在区间(𝑥-3s,𝑥+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天 生产的零件尺寸的均值与标准差.(精确到 0.01) 附:样本(xi,yi)(i=1,2,…,n)的样本相关系数 r= ∑ 𝑖=1 𝑛 (𝑥𝑖 -𝑥)(𝑦𝑖 -𝑦) √ ∑ 𝑖=1 𝑛 (𝑥𝑖 -𝑥) 2√ ∑ 𝑖=1 𝑛 (𝑦𝑖 -𝑦) 2 ,√0.008≈0.09. 解:(1)r= ∑ 𝑖=1 16 (xi -x)(𝑖-8.5) √ ∑ i=1 16 (𝑥𝑖 -𝑥) 2√ ∑ 𝑖=1 16 (𝑖-8.5) 2 = -2.78 0.212 ×√16×18.439 ≈-0.18. ∵|r|<0.25,∴可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大 或变小. (2)①∵𝑥=9.97,s≈0.212, ∴合格零件的尺寸范围是(9.334,10.606),显然第 13 号零件尺寸不在此范围之内, ∴需要对当天的生产过程进行检查

②别除离群值后,剩下数据的平均值为16×9.97-9.22)=10.02, 16 x=16×0.2122+16×9.972≈1591.134 =1 别除离群值后样本方差为×(1591.134-9.2-15×10.0220.008, ∴.剔除离群值后样本标准差为√0.0080.09
②剔除离群值后,剩下数据的平均值为 1 15 (16×9.97-9.22)=10.02, ∑ 𝑖=1 16 𝑥𝑖 2=16×0.2122+16×9.972≈1 591.134, ∴剔除离群值后样本方差为 1 15 ×(1 591.134-9.222 -15×10.022 )≈0.008, ∴剔除离群值后样本标准差为√0.008≈0.09