试卷代号:1009 座位号☐ 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本)试题 2009年1月 题 鸟 三 四 五 六 总 分 分 数 得 分 评卷人 一、单项选择题(每小题3分,本题共15分) 得分 1.若集合A={1,2},B={1,2,{1,2},则下列表述正确的是( A.ACB,且A∈B B.BCA,且A∈B C.ACB,且AEB D.A史B,且A∈B 得分 2.设有向图(a)、(b)、(c)与(d)如图一所示,则下列结论成立的是( (a) (b) (c) (d) 图一 A.(a)是强连通的 B.(b)是强连通的 C.(c)是强连通的 D.(d)是强连通的 得分 3.设图G的邻接矩阵为 0 11007 10 011 1 0000 01001 L0101 则G的边数为(). A.6 B.5 C.4 ).3 65
试卷代号:1009 座位号口口 中央广播电视大学2008-2009学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本) 试题 2009年 1月 题 夸- 四 五 六 总 分 分 数 得 分 评卷人 一、单项选择题(每小题 3分 .本题共 巧 分 ) }得州 卜若集合 A=(1,2),B=(1,2,(1,2)},则下列表述正确的是( A. ACB,且 AEB B. B(-A,且 AEB C. ACB,且 A任B D.A优B,且 AEB 匣亚口2·设有向图(。)、(。)、(。)与(、)如图一所示,则下列结论成立的是( 匡 · 日 · 囚 · 日 · 图 一 (b)是强连通的 (d)是强连通的 B. D 0州 卜 A. (a)是强连通的 C.(。)是强连通的 设图 G的邻接矩阵为 1 1 0 0 1 1 0 0 0 n U ﹄1] ︸ 1 0 0 1 1 0 1 0 则 G的边数为( A.6 C. 4 B. 5 D. 3

得分 无向简单图G是棵树,当且仅当( A,G连通且边数比结点数少1 B.G连通且结点数比边数少1 C.G的边数比结点数少1 D.G中没有回路 得分 5. 下列公式(·)为重言式. A.P∧aQ+PVQ B.(Q(PVQ))+(-QA(PVQ)) C.(P→(nQ+P))+(nP→(P+Q) D.(PV(P∧Q)+Q 得 分 评卷人 二、填空题(每小题3分,本题共15分) 得分 6. 命题公式P→(QVP)的真值是 得分 7.若图G=中具有一条汉密尔顿回路,则对于结点集V的每个非空子集 S,在G中删除S中的所有结点得到的连通分支数为W,则S中结点数{S引与W 满足的关系式为 得分 8.给定一个序列集合{000,001,01,10,0},若去掉其中的元素 ,则该序列集 合构成前缀码. 得分州 9.已知一棵无向树T中有8个结点,4度,3度,2度的分支点各一个,T的树叶数为 得分 10.(Hx)(P(x)+Q(x)VR(x,y)中的自由变元为 得 分 评卷人 三、逻辑公式翻译(每小题4分,本题共12分)】 得分列 11.将语句“他不去学校.”翻译成命题公式. 得分 12.将语句“他去旅游,仅当他有时间.”翻译成命题公式 得分 13.将语句“所有的人都学习努力.”翻译成命题公式。 66
1到口4·无向简单图G是棵树,当且仅当‘ A. G连通且边数比结点数少 C. G的边数 比结点数少 1 B. G连通且结点数比边数少 D. G中没有回路 匣王口5·二公式( ,为重言式 A. 一P八 ,Q'-' P V Q C. (P- (,Q-}P))H (,P- (P-Q) ) B. (Q- (P V Q))。 (,Q八(PVQ)) D.(,PV (PAQ))- Q 得 分 评卷人 二、填空题(每小题 3分,本题共 15分 ) 0州 } 0州 1 6.命题公式 尸~ (QV尸)的真值是 7.若图 G=中具有一条汉密尔顿回路,则对于结点集 V的每个非空子集 5,在 G中删除S中的所有结点得到的连通分支数为 W,则 5中结点数{引与 W 满足的关系式为 匣王口8·给定一个序列集合{000,001,01,10,0},若去掉其中的元素 ,则该序列集 合构成前缀码. 匣王口9·已知一棵无向树T中有8个结点,4度,3度,2度的分支点各一个,T的树叶数为 匣王口10. (V x) (P(x)-Q(x) V R(x,y),中的自由变元为 得 分 评卷人 三、逻辑公式翻译 (每小题 4分.本题共 12分 ) 11.将语句“他不去学校.”翻译成命题公式. 12.将语句“他去旅游 ,仅当他有时间.”翻译成命题公式. 13.将语句“所有的人都学习努力.”翻译成命题公式. - 洲 了人 - - 到 了人 - - 尸 了人 ︸ 户0 一 L ‘ - - L ﹄ 一 1 |卜 - 内匕

得分 评卷人 四、判断说明题(每小题7分,本题共14分)】 判断下列各题正误,并说明理由 得分 14.设N、R分别为自然数集与实数集,f:N-→R,f(x)=x+6,则f是单射. 得分 15.设G是一个有6个结点14条边的连通图,则G为平面图. 得分 评卷人 五、计算题(每小题12分,本题共36分) 得分 16.试求出(PVQ)→R的析取范式,合取范式,主合取范式. 得分 17.设A={a,b},1,2},B={a,b,1},1},试计算 (1)(A-B);(2)(AUB);(3)(AUB)-(A∩B). 得分 18.图G=,其中V={a,b,c,d,e},E={(a,b),(a,c),(a,e),(b,d),(b, e),(c,e),(c,d),(d,e)},对应边的权值依次为2、1、2、3、6、1、4及5,试 (1)画出G的图形; (2)写出G的邻接矩阵; (3)求出G权最小的生成树及其权值. 得分 评卷人 六、证明题(本题共8分) 得分 19.试证明集合等式A∩(BUC)=(A∩B)U(A∩C). 67
得 分 评卷人 四、判断说明题 (每小题 7分 .本题共 14分) 判断下列各题正误 ,并说 明理 由. 14州.} 0州 } 14.设 N,R分别为自然数集与实数集,f:N-R, f (x)=x十6,则 f是单射. 15.设 G是一个有 6个结点 14条边的连通图,则 G为平面图. 得 分 评卷人 五、计算题(每小题 12分.本题共 36分) 16.试求出(P V Q)-R的析取范式,合取范式,主合取范式. 17.设 A= Ha, b},1, 2},B={ a, b, {1},1},试计算 (1)(A一B);(2) (AUB);(3) (AUB)一 (AnB). 18.图 G=,其中V={ a, b,。,d, e},E={ (a, b), (a,。),(a,。),(b, d), (b, e), (c, e), (c, d), (d, e)},对应边的权值依次为2,1,2,3,6,1,4及 5,试 (1)画出 G的图形 ; (2)写出G的邻接矩阵; (3)求出G权最小的生成树及其权值. 画画 画 得 分 评卷人 六、证明题(本题共 8分) r4州 }19.试证明集合等式 An(BUC)=(AnB)U(AnC)

试卷代号:1009 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本)试题答案及评分标准 (供参考) 2009年1月 一、单项选择题(每小题3分,本题共15分) 1.A 2.D 3.B 4.A 5.C 二、填空题(每小题3分,本题共15分) 6.T(或填:1) 7.W≤IS 8.0 9.5 10.R(x,y)中的y 三、逻辑公式翻译(每小题4分,本题共12分) 11.设P:他去学校 (1分) P. (4分) 12.设P:他去旅游,Q:他有时间, (1分) P→Q. (4分) 13.设P(x):x是人,Q(x):x学习努力, (1分) (x)(P(x)+Q(x)). (4分) 四、判断说明题(每小题7分,本题共14分) 14.正确. (3分) 设x1,x2为自然数且x1≠x2,则有f(x)=x1十6≠x2+6=f(x2),故∫为单射. (7分) 15.错误. (3分) 不满足“设G是一个有v个结点e条边的连通简单平面图,若v≥3,则e≤3v一6”,(7分) 五、计算题(每小题12分,本题共36分》 16.(PVQ)+R台(PVQ)VR台(PAQ)VR(析取范式) (3分) 台(PVR)A(QVR)(合取范式) (6分) ((-PVR)V(QA-Q))A ((-QVR)V(PA-P)) 台(PVRVQ)A(PVRV-Q)∧(QVRVP)A(QVRV-P) 台(PVQVR)∧(PV-QVR)∧(PV-QVR)(主合取范式) (12分) 17.(1)(A-B)={{a,b},2} (4分) (2)(AUB)=({a,b},1,2,a,b,{1}} (8分) 68
试卷代号:1009 中央广播电视大学2008--2009学年度第一学期“开放本科”期末考试(半开卷) 离散数学(本) 试题答案及评分标准 (供参考) 2009年 1月 一、单项选择题(每小题 3分,本题共 15分) 1. A 2. D 3. B 4. A 5. C 二、填空题 (每小题 3分 ,本题共 15分) 6.T(或填 :1) 7. W<!Sl 8.0 9. 5 10. R(x,y)中的y 三、逻辑公式翻译(每小题 4分,本题共 12分) 11.设P:他去学校 (1分) 斤尸. (4分) 12.设P:他去旅游 ,Q:他有时间, (1分) P-,}Q. (4分) 13,设P(x);x是人 ,Q(、):二学习努力, (1分) (d x) (P(x)-Q(x)). (4分) 四、判断说明题(每小题 7分.本题共 14分) 14.正确. (3分) 设 XI , x:为自然数且 x, O:x2,则有 f(x,)=x1十6笋 x2+6=f(x2),故 f为单射. (7分) 15.错误. (3分) 不满足“设 G是一个有v个结点。条边的连通简单平面图,若 v) 3,则 。成3二一6". (7分) 五、计算题(每小题 12分,本题共36分) 16. (PV Q)-R a ,(PVQ)VRa (,PA -Q)VR(析取范式) (3分) a(-PVR)A (-QVR)(合取范式) (6分) }(<,PV R) V (Q八,Q))八 ((-QVR)V(P八,P)) a (,PVRVQ)八(,PVRV,Q) A (-QVRVP)A(一QVRV,P) a (-PVQVR)A(-PV -QVR)A (PV -QVR)(主合取范式) (12分) 17.(1) (A一B) ={{a, b},2} (4分) (2)(AUB)={{a,b},1,2,u,b,{1}} (8分) 68
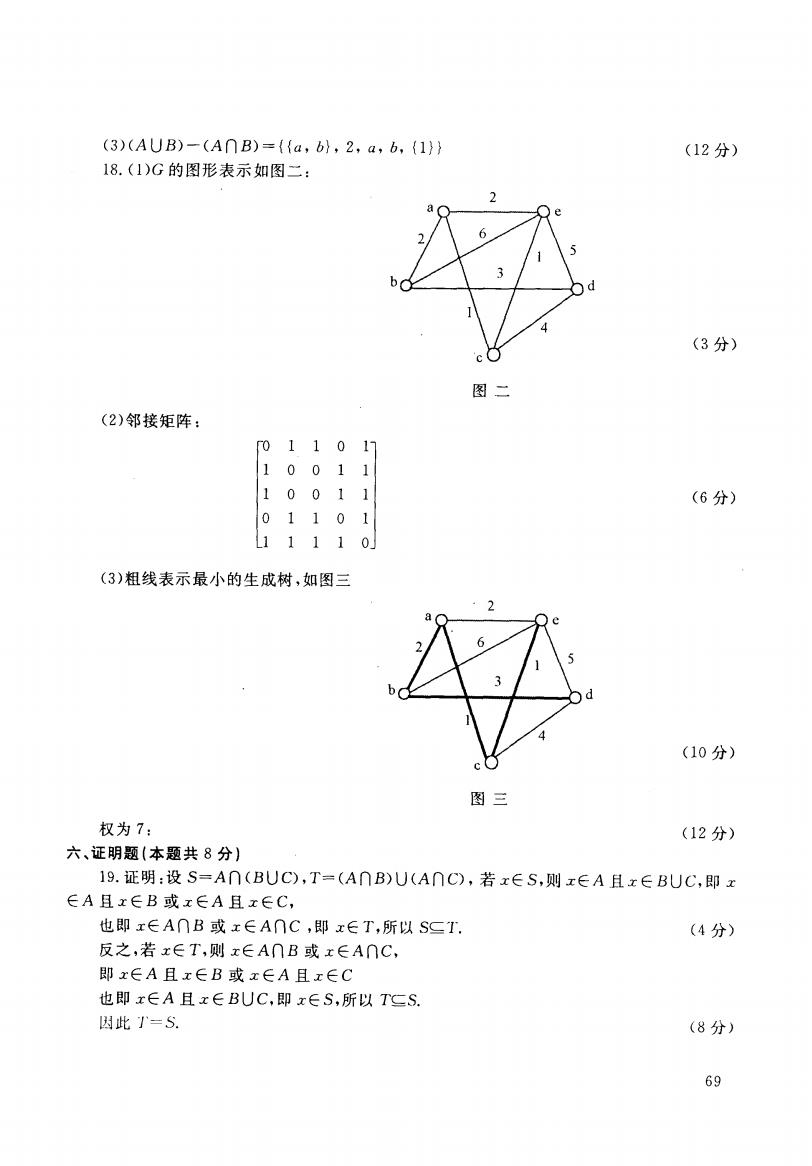
(3)(AUB)-(A∩B)={{a,b},2,a,b,{1}} (12分) 18.(1)G的图形表示如图二: 2 (3分) 图二 (2)邻接矩阵: 0 11017 100 11 1001 (6分) 01101 L11110 (3)粗线表示最小的生成树,如图三 (10分) 图三 权为7: (12分) 六、证明题(本题共8分) 19.证明:设S=A∩(BUC),T=(A∩B)U(A∩C),若x∈S,则x∈A且x∈BUC,即x ∈A且x∈B或x∈A且x∈C, 也即x∈A∩B或x∈A∩C,即x∈T,所以S二I. (4分) 反之,若x∈T,则x∈A∩B或x∈A∩C, 即x∈A且x∈B或x∈A且x∈C 也即x∈A且x∈BUC,即x∈S,所以T三S. 因此=S. (8分) 69
(3)(AUB)一(AnB)二{{a, b},2, a, b, {1}} 18. (1 )G的图形表示如图二 : (12分) (3分) 图 二 (2)邻接矩阵 : ﹃|| |l esle well ‘1| wees 11 11 1卫 1 ,.上 八曰 1 1 0 0 0 1 0 0 (6分) 1 1 0 1 1 1 (3)粗线表示最小的生成树 ,如图三 (10分) 图 三 权 为 7: 六、证明题 (本题共 8分) 19.证明 :设 S=An(BUC),T=(AnB)U(Anc) EA且xEB或 xEA且 xEC, 也即 xEAnB或 xEAnC ,即 xET,所以 SC 1'. 反之,若xET,则 xEAnB或 xEAnC, 即 xEA且 xEB或 xEA且 xEC 也即 xEA且 xEBUC,即 xES,所以 T9 S. 因此 了’=S. (12分 ) 若 XES,则 xEA且xEBUC,即 x (4分) (8分 ) 69