
《高等代数与解析几何(一)》课程教学大纲 大纲执笔人:韩艳英 大纲审核人:游兴中 课程编号:0701000205 英文名称:Advanced Algebra and Analytic Geometry 分:5 总学时:80。其中,讲授80 学时,实验0学时,上机0学时,实训0学时. 适用专业:数学与应用数学,信息与计算科学专业 先修课程:初等数学 一、课程性质与教学目的 本课程是数学专业和信息与计算科学专业一门重要的基础课,必修课。 本课程的教学目的是要求学生掌握高等代数与几何的基础知识,为进一步学习数学专业的其它 课程奠定基础。 《高代撕上与解折几何》是学的核心,出里积 。它的理论密切联系于数学的各个 领域,联系于科学技术的各个领域,构成它们的理论和方法基础。 无论学生要学任何后续理 工科课 程,也无论学生未来从事数学、科学的理论研究,或者未来从事实际技术工程工作,《高等代数与解析 几何》的基础都是至关重要的。通过本课程的教学,使学生不仅应把握代数与几何的基本概念,基 本理论,掌握基本思维方法,而且要能够应用这些基础知识进一步学习后续课程。本课程注重学生 对代数的基础概念、理论、和对矩阵、变换等的掌握,涵盖面较一般线性代数更加广泛和深入。 二、基本要求 本课程要求了解了解因式分解定理,并会利用它求最大公因式,了解有理系数多项式的概念, 行列式的概念,拉普拉斯定理,guass消元法,n维向量空间n维向量的概念,矩阵分块乘法的初等变 换方法,了解混合积,平面束,平面曲线的方程、曲面的方程、空间曲线的方程的概念,理解母线 平行于坐标轴的柱面方程的形式。了解椭球面,双曲面,抛物面的方程的一般形式。 理解一元多项式、整除的概念,掌握整除的性质。理解最大公因式及互素的概念,掌握最大公 因式求法。掌握重因式概念,能求重因式。理解多项式函数的概念,掌握复系数与实系数多项式的 因式分解。掌握有理系数多项式有理根的求法及用Eisenstein判别法判别有理数域上多项式的不可约 性。 掌握行列式的性质并能够熟练应用行列式的性质计算行列式,熟练掌握克兰姆法则解 方程组。理解向量组线性相关、线性无关的定义,掌握有关向量组线性相关、线性无关的有关性质 及判别法。正确理解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组 及秩。理解向量组等价的概念、向量组的秩与矩阵秩的关系。掌握齐次线性方程组有非零解的充要 条件及非齐次线性方程组有解的充要条件。会熟练求解齐次线性方程组的基础解系、通解及解空 间、以及非齐次线性方程组的通解,理解非齐次线性方程组的解的结构及通解的概念。 熟练掌握用行初等变换求线性方程组通解的方法。 正确理解矩阵的概念,了解一些特殊的矩阵及它们的性质。掌握矩阵的运算及运算规律,了解 矩阵乘积的行列式与秩。理解逆矩阵的概念,掌握逆矩阵的性质及矩阵可逆的条件。理解矩阵分块 的意义,能利用分块矩阵简化矩阵的运算。理解初等矩阵的概念,掌握初等矩阵与矩阵的初等变换 的对应关系,掌握用初等变换求一个可逆矩阵的逆矩阵方法。 掌握矢量的概念、运算,线性关系,分解,射影,数性积,矢性积
《高等代数与解析几何(一)》课程教学大纲 大纲执笔人:韩艳英 大纲审核人:游兴中 课程编号:0701000205 英文名称:Advanced Algebra and Analytic Geometry 学 分: 5 总 学 时:80。其中,讲授 80 学时,实验 0 学时,上机 0 学时,实训0 学时。 适用专业: 数学与应用数学,信息与计算科学专业 先修课程:初等数学 一、课程性质与教学目的 本课程是数学专业和信息与计算科学专业一门重要的基础课,必修课。 本课程的教学目的是要求学生掌握高等代数与几何的基础知识,为进一步学习数学专业的其它 课程奠定基础。《高等代数与解析几何》是数学的核心基础课程。它的理论密切联系于数学的各个 领域, 联系于科学技术的各个领域, 构成它们的理论和方法基础. 无论学生要学任何后续理工科课 程, 也无论学生未来从事数学、科学的理论研究, 或者未来从事实际技术工程工作, 《高等代数与解析 几何》的基础都是至关重要的。通过本课程的教学,使学生不仅应把握代数与几何的基本概念,基 本理论,掌握基本思维方法,而且要能够应用这些基础知识进一步学习后续课程。本课程注重学生 对代数的基础概念、理论、和对矩阵、变换等的掌握, 涵盖面较一般线性代数更加广泛和深入。 二、基本要求 本课程要求了解了解因式分解定理,并会利用它求最大公因式,了解有理系数多项式的概念, 行列式的概念,拉普拉斯定理,guass消元法,n维向量空间n维向量的概念,矩阵分块乘法的初等变 换方法,了解混合积,平面束,平面曲线的方程、曲面的方程、空间曲线的方程的概念,理解母线 平行于坐标轴的柱面方程的形式。了解椭球面,双曲面,抛物面的方程的一般形式。 理解一元多项式、整除的概念,掌握整除的性质。理解最大公因式及互素的概念,掌握最大公 因式求法。掌握重因式概念,能求重因式。理解多项式函数的概念,掌握复系数与实系数多项式的 因式分解。掌握有理系数多项式有理根的求法及用Eisenstein判别法判别有理数域上多项式的不可约 性。 掌握行列式的性质并能够熟练应用行列式的性质计算行列式,熟练掌握克兰姆法则解 方程组。理解向量组线性相关、线性无关的定义,掌握有关向量组线性相关、线性无关的有关性质 及判别法。正确理解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组 及秩。理解向量组等价的概念、向量组的秩与矩阵秩的关系。掌握齐次线性方程组有非零解的充要 条件及非齐次线性方程组有解的充要条件。会熟练求解齐次线性方程组的基础解系、通解及解空 间、以及非齐次线性方程组的通解,理解非齐次线性方程组的解的结构及通解的概念。 熟练掌握用行初等变换求线性方程组通解的方法。 正确理解矩阵的概念,了解一些特殊的矩阵及它们的性质。掌握矩阵的运算及运算规律,了解 矩阵乘积的行列式与秩。理解逆矩阵的概念,掌握逆矩阵的性质及矩阵可逆的条件。理解矩阵分块 的意义,能利用分块矩阵简化矩阵的运算。理解初等矩阵的概念,掌握初等矩阵与矩阵的初等变换 的对应关系,掌握用初等变换求一个可逆矩阵的逆矩阵方法。 掌握矢量的概念、运算,线性关系,分解,射影,数性积,矢性积

能熟练求出平面的方程,空间直线的方程,掌握平面与点的位置关系,两平面的相关位置,,直 线与平面的相关位置,空间两直线的相关位置,空间直线与点的位置关系,。理解柱面、锥面、旋 转曲面的概念及其方程的形式,掌握母线平行于坐标轴的柱面、锥面、旋转曲面的方程的求法。 三、重点与难点 重点内容:最大公因式及互素的概念,掌握最大公因式求法,多项式整除及利用因式分解定理, 求最大公因式,重因式的概念和计算,行列式的定义,利用行列式的性质和行列式展开定理计算行 列式,克兰姆法则,线性方程组解的判定及解的结构,向量组的线性相关性以及极大线性无关组的 计算,矩阵的乘积,初等矩阵,矩阵的逆,平面的方程,平面与点的位置关系,两平面的相关位 置,空间直线的方程,直线与平面的相关位置,空间两直线的相关位置,空间直线与点的位置关 系。 难点内容:行列式的计算,矩阵的秩的概念及计算,矩阵的逆的计算,分块矩阵,维向量空 间、向量的线性相关性,利用平面束解题,二次曲面的方程及图形 四、教学方法 以课堂讲授为主,结合课堂讨论教学,问题教学法,探究性教学法,并辅助有课后作业。 五、课程知识单元、知识点及学时分配 知识单元 知识点 序号 描述 序号 描述 课 1 勒域 23 元多项式及整除的概念 最大公因式 多项式 因式分解定理 5 重因式 多项式函数 6 复系数与夹整武分解及 排列,行列式的定义 行列式的性质和计算 行列式 行列式按 一行(列)展开 兰婚法则 消元 线性方程组 n维向量空间,向量的线性相关性 18 矩阵的秩 线性方程组有解的判别及解的结构 矩阵及其运算 矩阵乘积的行列式与秩 矩阵 矩阵的递 6 矩阵的分块及初等矩阵 矢量及其运算 矢量与坐标 两矢量的数性积, 平面曲线的方程、曲面的 5 轨迹与方程 母线平行于坐标轴的柱面方程 空间曲线的方程 6 平曲万程 6 2 平面与点的相关位置 两平面的相关 位置
能熟练求出平面的方程,空间直线的方程,掌握平面与点的位置关系,两平面的相关位置,,直 线与平面的相关位置,空间两直线的相关位置,空间直线与点的位置关系,。理解柱面、锥面、旋 转曲面的概念及其方程的形式,掌握母线平行于坐标轴的柱面、锥面、旋转曲面的方程的求法。 三、重点与难点 重点内容:最大公因式及互素的概念,掌握最大公因式求法,多项式整除及利用因式分解定理, 求最大公因式,重因式的概念和计算,行列式的定义,利用行列式的性质和行列式展开定理计算行 列式,克兰姆法则,线性方程组解的判定及解的结构,向量组的线性相关性以及极大线性无关组的 计算,矩阵的乘积,初等矩阵,矩阵的逆,平面的方程,平面与点的位置关系,两平面的相关位 置,空间直线的方程,直线与平面的相关位置,空间两直线的相关位置,空间直线与点的位置关 系。 难点内容:行列式的计算,矩阵的秩的概念及计算,矩阵的逆的计算,分块矩阵,n维向量空 间、向量的线性相关性,利用平面束解题,二次曲面的方程及图形。 四、教学方法 以课堂讲授为主,结合课堂讨论教学,问题教学法,探究性教学法,并辅助有课后作业。 五、课程知识单元、知识点及学时分配 知识单元 知识点 讲 序号 描述 序号 描述 课 1 多项式 1 数域 18 2 一元多项式及整除的概念 3 最大公因式 4 因式分解定理 5 重因式 多项式函数 6 复系数与实系数多项式的因式分解及 有理系数多项式 1 行列式 1 排列,行列式的定义 12 2 行列式的性质和计算 3 行列式按一行(列)展开 4 克兰姆法则 2 线性方程组 1 消元法 18 2 n维向量空间,向量的线性相关性 3 矩阵的秩 4 线性方程组有解的判别及解的结构 3 矩阵 1 矩阵及其运算 16 2 矩阵乘积的行列式与秩 3 矩阵的逆 4 矩阵的分块及初等矩阵 4 矢量与坐标 1 矢量及其运算 2 矢量的线性关系与矢量的分解,射影 4 3 两矢量的数性积,矢性积 5 轨迹与方程 1 平面曲线的方程、曲面的方程 2 母线平行于坐标轴的柱面方程 4 3 空间曲线的方程 6 平面与空间 直线 1 平面方程 6 2 平面与点的相关位置,两平面的相关 位置

知识单元 知识点 讲 序号 描述 序号 描述 3 空间直线的方程 直线与平面,直线与点及空间两直线 的相关位置 平面束 柱面、锥 面、旋转曲 柱面、锥面、旋转曲面 7 2 面与二次曲 椭球面、双曲面、抛物面 8 总计 80 六、实验、上机与实训教学条件及内容 无 七、作业要求 本课程要求学生必须独立做大量的题目才能更好地掌握所学内容,要求学生必须完成课本基本习 题,有能力的学生可适当完成一些补充题目。 八、考核方式与要求 1知识考核 占总成绩的80%,主要采用期末书面考试的方式评定。期未考试采用闭卷考试。 2.能力考核 占总成绩的20%,其中根据作业、质疑、课堂讨论和自由选题报告等能力、素质评定占20%。 九、教材与主要参考书 1.推荐教材: [1]北京大学数学系几何与代数教研室代数小组.高等代数.高等教育出版社,2003 [2]吕林根,许子道.解析几何 高等教育出版社,2001 2.主要参考书: [1]杨子胥.高等代数习题解.山东科学技术出版社,2001 [2]钱吉林.高等代数题解精粹.中央民族大学出版社,2002 [3]王萼芳.高等代数[00.高等教有出版社,2009
知识单元 知识点 讲 序号 描述 序号 描述 课 3 空间直线的方程 4 直线与平面,直线与点及空间两直线 的相关位置 5 平面束 7 柱面、锥 面、旋转曲 面与二次曲 面 1 柱面、锥面、旋转曲面 2 2 椭球面、双曲面、抛物面 8 总计 80 六、实验、上机与实训教学条件及内容 无 七、作业要求 本课程要求学生必须独立做大量的题目才能更好地掌握所学内容,要求学生必须完成课本基本习 题,有能力的学生可适当完成一些补充题目。 八、考核方式与要求 1.知识考核 占总成绩的80%,主要采用期末书面考试的方式评定。期末考试采用闭卷考试。 2.能力考核 占总成绩的20%,其中根据作业、质疑、课堂讨论和自由选题报告等能力、素质评定占20%。 九、教材与主要参考书 1.推荐教材: [1] 北京大学数学系几何与代数教研室代数小组.高等代数.高等教育出版社,2003 [2] 吕林根,许子道.解析几何 高等教育出版社,2001 2.主要参考书: [1] 杨子胥.高等代数习题解.山东科学技术出版社,2001 [2] 钱吉林.高等代数题解精粹.中央民族大学出版社,2002 [3] 王萼芳.高等代数[M].高等教育出版社,2009

《高等代数与解析几何(二)》课程教学大纲 大纲执笔人:韩艳英 大纲审核人:游兴中 课程编号:0701000195 英文名称:Advanced Algebra and Analytic Geometry 学 分:5 总学时:80 。其中,讲授80学时,实验0学时,上机0学时,实训0学 适用专业:数学与应用数学,信息与计算科学专业 先修课程:初等数学、高等代数与解析几何(一) 一、课程性质与教学目的 本课程是数学专业和信息与计算科学专业一门重要的基础课,必修课。 本课程的教学目的是要求学生掌握高等代数与几何的基础知识,为进一步学习数学专业的其它课 程奠定基础。《高等代数与解析几何》是数学的核心基础课程。它的理论密切联系于数学的各个领 域,联系于科学技术的各个领域,构成它们的理论和方法基础无论学生要学任何后续理工科课程,也 无论学生未来从事数学、科学的理论研究,或者未来从事实际技术工程工作 《高等代数与解析几 何》的基础都是至关重要的。通过本课程的教学,使学生不仅应把握代数与几何的基本概念,基本 理论,掌握基本思维方法,而且要能够应用这些基础知识进一步学习后续课程。本课程注重学生对 代数的基础概念、理论、和对矩阵、变换等的掌握,涵盖面较一般线性代数更加广泛和深入。 二、基本要求 本课程要求了解二次型秩的概念,了解二次型的标准形、规范形的概念,了解惯性定理。了解用 配方法化二次型为标准形的方法,了解线性空间同构的意义及基本性质,了解线性变换的值域、 核、秩与零度的概念,了解不变子空间概念,了解欧氏空间的定义及基本性质。了解正交变换的意 义。 掌握二次型及其矩阵表示,掌握用合同变换化二次型为标准形(或规范形)的方法。掌握二次型 和对应矩阵的正定性及其判别法。正确理解线性空间的概念,掌握其性质。理解维线性空间、维 数、基与坐标等概念。掌握基变换和坐标变换公式,会求过渡矩阵。了解线性子空间概念及子空间 的运算,掌握维数公式及子空间直和分解的条件。理解线性变换的定义及线性变换的运算等概念。 理解线性变换的矩阵概念,学握线性变换的运算与对应基下矩阵运算之间的关系,以及矩阵相似等 概念。理解特征值与特征向量概念,会求一个线性变换的特征值、特征向量。掌握矩阵相似于对角 形的条件,会求己给矩阵的相似标准形。理解有关线性变换的秩与零度的关系。理解不变子空间与 线性变换矩阵化简之间的关系。理解标准正交基的意义,掌握从已知基求标准正交基的方法。理解 正交变换与正交矩阵之间的关系,掌握正交矩阵的一些基本性质。理解欧氏空间中子空间正交的概 念及空间的正交分解。理解对称矩阵与对称变换的关系、对称矩阵的性质,会求对称矩阵在正交合 同意义下的标准形,用正交的线性替换化实二次型为标准形。 三、重点与难点 重点内容:用配方法化二次型为标准形的方法,掌握用合同变换化二次型为标准形(或规范形 的方法。正定二次型。线性空间的概念,性质,维数,基与坐标,基变换和坐标变换公式,过渡矩
《高等代数与解析几何(二)》课程教学大纲 大纲执笔人:韩艳英 大纲审核人:游兴中 课程编号:0701000195 英文名称:Advanced Algebra and Analytic Geometry 学 分: 5 总 学 时:80 。其中,讲授 80 学时,实验 0 学时,上机 0 学时,实训0 学 时。 适用专业: 数学与应用数学,信息与计算科学专业 先修课程:初等数学、高等代数与解析几何(一) 一、课程性质与教学目的 本课程是数学专业和信息与计算科学专业一门重要的基础课,必修课。 本课程的教学目的是要求学生掌握高等代数与几何的基础知识,为进一步学习数学专业的其它课 程奠定基础。《高等代数与解析几何》是数学的核心基础课程。它的理论密切联系于数学的各个领 域, 联系于科学技术的各个领域, 构成它们的理论和方法基础. 无论学生要学任何后续理工科课程, 也 无论学生未来从事数学、科学的理论研究, 或者未来从事实际技术工程工作, 《高等代数与解析几 何》的基础都是至关重要的。通过本课程的教学,使学生不仅应把握代数与几何的基本概念,基本 理论,掌握基本思维方法,而且要能够应用这些基础知识进一步学习后续课程。本课程注重学生对 代数的基础概念、理论、和对矩阵、变换等的掌握, 涵盖面较一般线性代数更加广泛和深入。 二、基本要求 本课程要求了解二次型秩的概念,了解二次型的标准形、规范形的概念,了解惯性定理。了解用 配方法化二次型为标准形的方法,了解线性空间同构的意义及基本性质,了解线性变换的值域、 核、秩与零度的概念,了解不变子空间概念,了解欧氏空间的定义及基本性质。了解正交变换的意 义。 掌握二次型及其矩阵表示,掌握用合同变换化二次型为标准形(或规范形)的方法。掌握二次型 和对应矩阵的正定性及其判别法。正确理解线性空间的概念,掌握其性质。理解n维线性空间、维 数、基与坐标等概念。掌握基变换和坐标变换公式,会求过渡矩阵。了解线性子空间概念及子空间 的运算,掌握维数公式及子空间直和分解的条件。理解线性变换的定义及线性变换的运算等概念。 理解线性变换的矩阵概念,掌握线性变换的运算与对应基下矩阵运算之间的关系,以及矩阵相似等 概念。理解特征值与特征向量概念,会求一个线性变换的特征值、特征向量。掌握矩阵相似于对角 形的条件,会求已给矩阵的相似标准形。理解有关线性变换的秩与零度的关系。理解不变子空间与 线性变换矩阵化简之间的关系。理解标准正交基的意义,掌握从已知基求标准正交基的方法。理解 正交变换与正交矩阵之间的关系,掌握正交矩阵的一些基本性质。理解欧氏空间中子空间正交的概 念及空间的正交分解。理解对称矩阵与对称变换的关系、对称矩阵的性质,会求对称矩阵在正交合 同意义下的标准形,用正交的线性替换化实二次型为标准形。 三、重点与难点 重点内容:用配方法化二次型为标准形的方法,掌握用合同变换化二次型为标准形(或规范形) 的方法。正定二次型。线性空间的概念,性质,维数,基与坐标,基变换和坐标变换公式,过渡矩
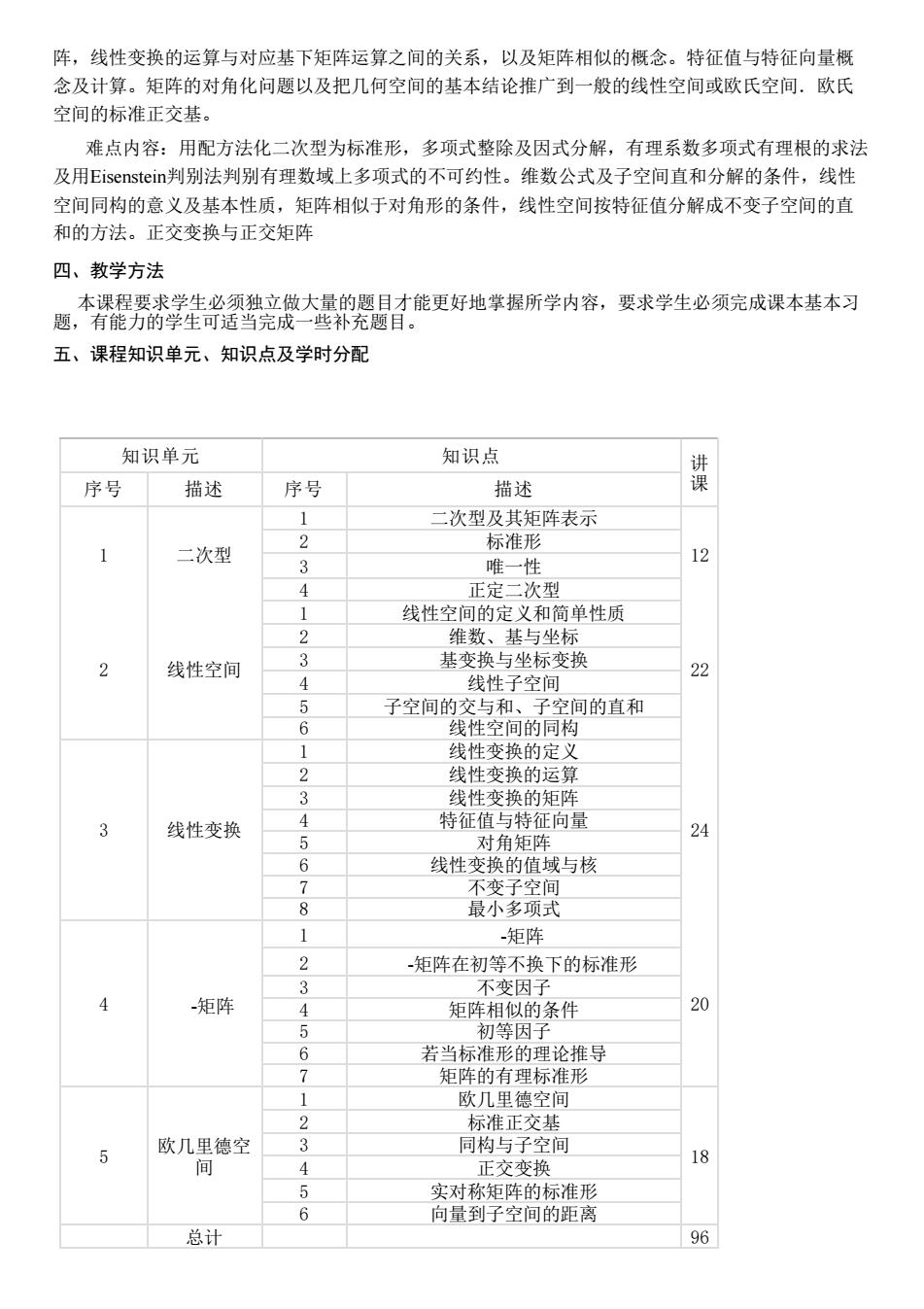
阵,线性变换的运算与对应基下矩阵运算之间的关系,以及矩阵相似的概念。特征值与特征向量概 念及计算。矩阵的对角化问题以及把几何空间的基本结论推广到一般的线性空间或欧氏空间.欧氏 空间的标准正交基。 难点内容:用配方法化二次型为标准形,多项式整除及因式分解,有理系数多项式有理根的求法 及用Eisenstein判别法判别有理数域上多项式的不可约性。维数公式及子空间直和分解的条件,线性 空间同构的意义及基本性质,矩阵相似于对角形的条件,线性空间按特征值分解成不变子空间的直 和的方法。正交变换与正交矩阵 四、教学方法 题,本学鞋等售亮设大漫盟能更好地苹提所学内容。要求学生必须完成课本基本习 五、课程知识单元、知识点及学时分配 知识单元 知识点 序号 描述 序号 描述 次型及其矩阵表示 二次型 标准形 3 唯一性 正定一次型 线性空间的定义和简单性质 维数、 基与坐标 2 线性空间 基变换与坐标变换 线性子空间 22 5 6 子 线性变换的矩阵 线性变换 特征值与特征向量 对角矩阵 24 线性变换的值域与核 矩阵 矩阵在初等不换下的标准形 不变因子 矩阵 矩阵相似的条件 90 初等因 若当标准形的理论推导 矩阵的有理标准形 欧几里德空间 标准正交基 欧几里德空 同构与子空间 间 正交变换 实对称矩阵的标准形 向量到子空间的距离 总计 96
阵,线性变换的运算与对应基下矩阵运算之间的关系,以及矩阵相似的概念。特征值与特征向量概 念及计算。矩阵的对角化问题以及把几何空间的基本结论推广到一般的线性空间或欧氏空间.欧氏 空间的标准正交基。 难点内容:用配方法化二次型为标准形,多项式整除及因式分解,有理系数多项式有理根的求法 及用Eisenstein判别法判别有理数域上多项式的不可约性。维数公式及子空间直和分解的条件,线性 空间同构的意义及基本性质,矩阵相似于对角形的条件,线性空间按特征值分解成不变子空间的直 和的方法。正交变换与正交矩阵 四、教学方法 本课程要求学生必须独立做大量的题目才能更好地掌握所学内容,要求学生必须完成课本基本习 题,有能力的学生可适当完成一些补充题目。 五、课程知识单元、知识点及学时分配 知识单元 知识点 讲 序号 描述 序号 描述 课 1 二次型 1 二次型及其矩阵表示 12 2 标准形 3 唯一性 4 正定二次型 2 线性空间 1 线性空间的定义和简单性质 22 2 维数、基与坐标 3 基变换与坐标变换 4 线性子空间 5 子空间的交与和、子空间的直和 6 线性空间的同构 3 线性变换 1 线性变换的定义 24 2 线性变换的运算 3 线性变换的矩阵 4 特征值与特征向量 5 对角矩阵 6 线性变换的值域与核 7 不变子空间 8 最小多项式 4 -矩阵 1 -矩阵 20 2 -矩阵在初等不换下的标准形 3 不变因子 4 矩阵相似的条件 5 初等因子 6 若当标准形的理论推导 7 矩阵的有理标准形 5 欧几里德空 间 1 欧几里德空间 18 2 标准正交基 3 同构与子空间 4 正交变换 5 实对称矩阵的标准形 6 向量到子空间的距离 总计 96

六、实验、上机与实训教学条件及内容 无 七、作业要求 要求必须完成课本基本习题,有能力的学生可适当完成一些补充题目。 八、考核方式与要求 1.知识考该 占总成绩的80%,主要采用期末书面考试的方式评定。期未考试采用闭卷考试。 2.能力考核 占总成绩的20%,其中根据作业、质疑、课堂讨论和自由选题报告等能力、素质评定占20%。 九、教材与主要参考书 1.推荐教材 [1]北京大学数学系几何与代数教研室代数小组.高等代数.高等教有出版社,2003 [2]吕林根,许子道.解析几何高等教育出版社,2001 2.主要参考书: [1]杨子胥.高等代数习题解.山东科学技术出版社,2001 [2]钱吉林.高等代数题解精粹.中央民族大学出版社,2002 [3)]王萼芳.高等代数M.高等教有出版社,2009
六、实验、上机与实训教学条件及内容 无 七、作业要求 要求必须完成课本基本习题,有能力的学生可适当完成一些补充题目。 八、考核方式与要求 1.知识考核 占总成绩的80%,主要采用期末书面考试的方式评定。期末考试采用闭卷考试。 2.能力考核 占总成绩的20%,其中根据作业、质疑、课堂讨论和自由选题报告等能力、素质评定占20%。 九、教材与主要参考书 1.推荐教材: [1] 北京大学数学系几何与代数教研室代数小组.高等代数.高等教育出版社,2003 [2] 吕林根,许子道.解析几何 高等教育出版社,2001 2.主要参考书: [1] 杨子胥.高等代数习题解.山东科学技术出版社,2001 [2] 钱吉林.高等代数题解精粹.中央民族大学出版社,2002 [3] 王萼芳.高等代数[M].高等教育出版社,2009