
第四章 矩阵的分解 本章我们主要讨论矩阵的四种分解:矩 阵的三角分解,QR分解,满秩分解,奇异 值分解。 4.1 矩阵的三角分解 4.1.1 三角分解及其存在唯一性问题 定义4.1设 A∈C"”,如果存在下三角矩阵 L∈C""和上三角矩阵 U∈C"" 使得A=LU, 则称A可以作三角分解。 This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

定理4.1设A∈Cm",则A有三角分解的充要条件 是A的各阶顺序主子式△,…△均不为零, 定理表明并不是每个可逆矩阵都可以作三角 分解。如 01 A= 10 不能作三角分解。 定理4.2设A∈C”,且A的前r个顺序主子式不为零, 即△k≠0(k=1,2,…,r),则A可以作三角分解, 证明:A= (A.A2A Az A,A2)(BABA2
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

上述定理只是充分条件,如: 00)=0011)_0011 12气11八01(12八0 矩阵的三角分解不唯一,如A=LU=(LD)(DU), 其中D为可逆的对角矩阵 定义4.2将L是单位下三角矩阵的LU三角分解 称为矩阵的Doolittle分解。将U是单位上三角 矩阵的LU三角分解称为矩阵的Crout分解。若 A=LDR,其中L是单位下三角矩阵,D是对角 矩阵,U是单位上三角矩阵,则称为A的LDR 分解。 This document is produced bytriaversion of PrinFah Visit www.printfash for more infomation
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

定理4.3设A为n阶非奇异矩阵,则A有唯一LDR分解 的充要条件是A的各阶顺序主子式△,…△均不为零. 此时,D=diag(d,d,,dn)的元素满足 4=△,4=Ak=2.…以 推论设A为n阶非奇异矩阵,则A有唯一的Doolittle分解或 Crout2分解的充要条件是A的各阶顺序主子式△,…△均不为零. 4.1.2三角分解的紧凑计算格式 计算Doolittle分解:以n=3为例 This documentis prduced byriaversion ofPrnh Visit www.prinashcfor more informion
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

47 4243 422 21 1 u22 23 a33 2412 3 12141 121412+u2 1243+423 1312411131412+132u22 13i413+132423+33 由a,=4,→4,=4,(j=1,2,3) 由a=4h1→41=24:41=4k1→41=4 141 由a22=242+42→42=a2-l2142a23=l214g+423→423=a23-h214 由aa=%14a+l→a--42 1422 由a3=131413+l32423+43→43=43-(3143+l2423)
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

定理4.4设A∈Cm"是Hermite.正定矩阵,则存在下 三角矩阵L∈Cx",使得A=LL,称为A的Cholesky分解。 以n=3为例 [a1a2 937 d 2 a23 121 l22 as a32 13112 1 k 42 11 =42141h2+1zf 1☑21l1+12l2 g141g1+122h+h2+ha月 This documentis prduced byria version ofPrnhVisit www.prinashcfor more informion
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

Ax=b→L(UX)=b三 Ly=b Ux=y 例.试用Doolittle分解求解方程组 2 -6 10 13 -19 19 -6 -3 -6Lx3] -30 2 5 -6 「1 0 04 42 413 3 -19 0 V22 2423 -6 -3 6 12 133」 This documentis produced bytril versinofPrVisit www.prinashmformore infomio
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information
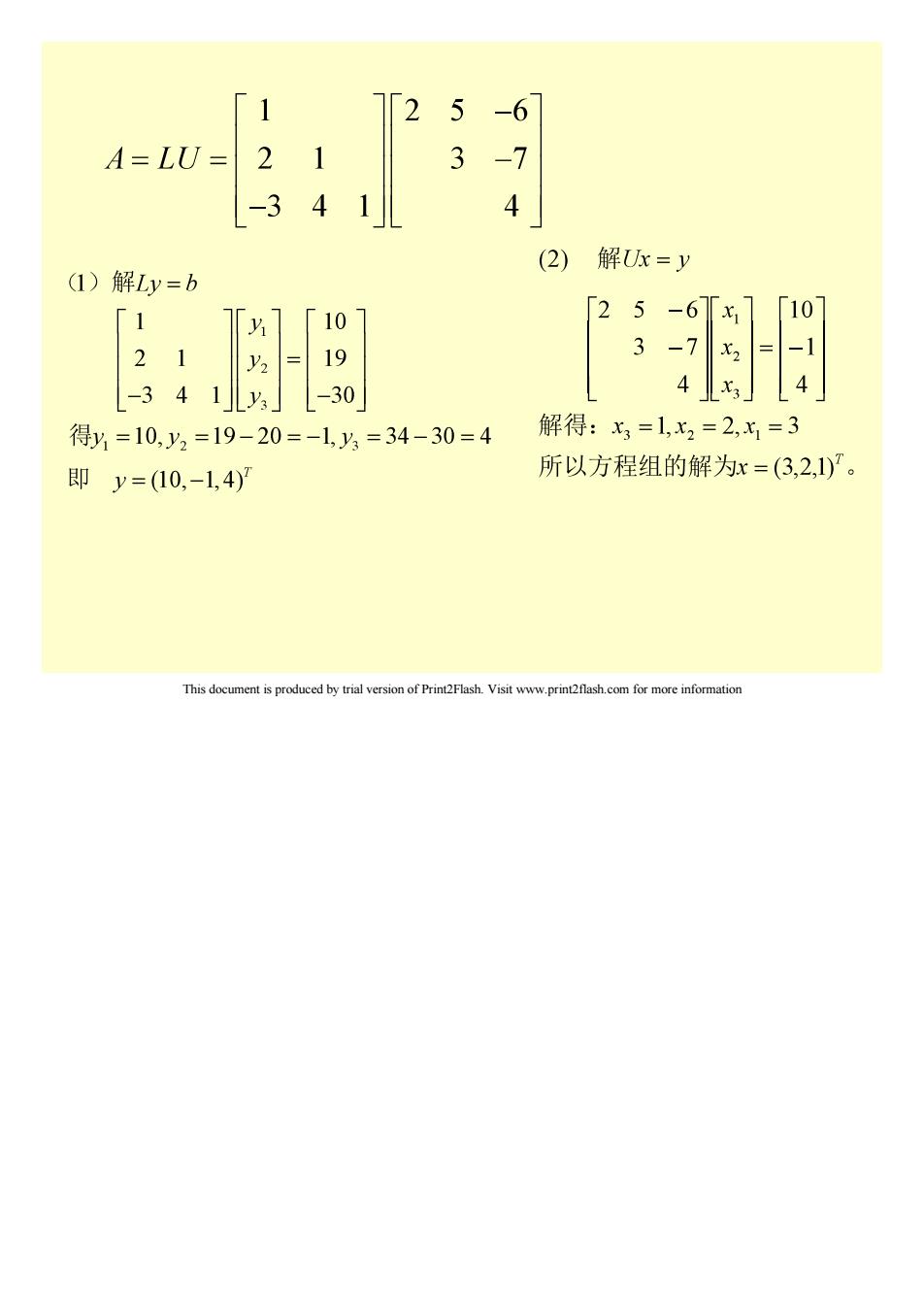
7「2 -6 A=LU= 21 3-7 -341 4 (2)解Ux=y (1)解Ly=b 1 7y1「10 21 y2 19 1-341y」-30」 得y=10,y2=19-20=-1,y=34-30=4 解得:x3=1,x2=2,x=3 即y=10,-1,4) 所以方程组的解为x=(3,2,1)。 This documentis prduced byria version ofPrnhVisit www.prinashcfor more informion
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

练习1:将A分解为A=LU,其中L为单位 下三角矩阵,U为上三角矩阵: 22 23 4= =LU 6 练习2:将A分解为A=L,其中L为正线 下三角矩阵。 This document is produced by trial version of Print2Flash Visit www.print2flash.com for more informatio
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

4.2矩阵的QR分解 定义:设A∈Cx”,如果存在n阶酉矩阵Q 和n阶上三角矩阵R,使得A=OR 则称之为A的QR分解或酉-三角分解。当 A∈Rx”时,称为A的正交三角分解。 定理4.5任意A∈Cmx”都可以作QR分解。 定理4.6设A∈C”,则A可唯一分解为 A=OR 其中Q是n阶酉矩阵,R∈C"是具有正对角元的 上三角矩阵
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information