
7D-6s Prediction of LC-VCOs'Tuning Curves with Period Calculation Technique Zhangwen Tang,Jie He,Hongyan Jian,Haiqing Zhang,Jie Zhang,and Hao Min ASIC System State Key Laboratory,Fudan University,Shanghai 200433,P.R.China Tel:+86-21-65642765*819Fax:+86-21-65644158 E-mail:(zwtang,jiehe,hyjian,hmin)@fudan.edu.cn Abstract-This paper describes a new prediction method of tuning curves of a LC-tank voltage-controlled oscillator (VCO) with period calculation technique.With this period calculation technique,the prediction of oscillator tuning curves is more accurate compared with the traditional harmonic approxi -mation.The theoretical analyses are experimentally validated with a CMOS complementary LC-tank VCO implemented in 0.35um 1P4M pure logic CMOS process. L.INTRODUCTION n The complementary cross-coupled negative-Gm LC-tank oscillator is shown in Fig.1,which employs both NMOS and PMOS cross-coupled pairs.Many published papers [1]-[4],have employed this type of LC-tank VCO,but oscillator tuning curves were obtained from SPICE simulations or measurements.The prediction of oscillator Fig.1.CMOS complementary cross-coupled LC-tank VCO tuning curves is quite challenging due to highly nonlinear characteristics of varactors.A numerical method is shown in II.HARMONIC APPROXIMATION OF LC TANK IN [2],but it is quite complex and time-consuming.The tuning FREQUENCY DOMAIN curves must be numerically computed again if the bias current changes.M.Tiebout [3]and R.L.Bunch [4]et al.also Traditional small-signal analysis is not suitable for found large-signal effects to the instantaneous capacitance of LC-tank oscillators with large-amplitude swings [2-5].The large-signal effect must be considered.Thus,the effective LC-tank,but their analyses were only qualitative.The recent papers in [5]and [6],introduced the notion of effective capacitance calculation of LC-tank circuit is not a simple capacitance across the amplitude of oscillation,and time-average process.In this section,we will briefly present presented an analytical solution to tank balance equation. how to calculate the effective capacitance through large Their approach was simple,but inaccurate since the second -signal nonlinear analysis of varactors in a serial LC-tank and higher order harmonics were neglected.Note that circuit [2],[4]-[6]. oscillating voltage in LC tank is not an ideal sinusoid [2],the The presence of on-chip inductors in Fig.I imposes that effective capacitance of step-like varactors driven by a the dc value of differential oscillating voltages has to be a sinusoid is not the actual effective one in a true LC-tank constant voltage Vdc.Neglecting the tank losses in on-chip VCO. inductors and varactors,the half circuit of LC-tank VCO can be considered as a serial LC-tank structure (Fig.2(a))[6]. Recently,the design and modeling of on-chip MOS varactors is a hot topic.However,these researches are The oscillating voltage waveform can be represented as a focusing on how to implement MOS varactors with high Fourier series: quality and large tuning range on standard Silicon CMOS V0=6+22A.cos(nor) (1) technology.Few of them deal with the large-signal analyses, nonlinear effect to C-V curves and tuning curves of LC-tank And,small-signal capacitance of varactors can be denoted as In Section II,the harmonic approximation method of the a Fourier series in time domain: large-signal nonlinearity of varactors is briefly recalled,and the effective capacitance of LC tank is calculated.Section III C.(Ve)=C+2Ccos(not) (2) investigates I-V locus of step-like MOS varactors in a serial m=l LC-tank and predicts the tuning curves through the where C is the Fourier coefficient at nth order harmonic. calculation of oscillating period of a LC tank in time domain. Since serial LC-tank circuits must satisfy the Kirchhoffs In Section IV,our prediction method in time domain is laws,the inductor current must equal varactor current compared with the harmonic approximation in frequency domain.Lastly,the theoretical analyses are experimentally 1,=→y0h=C.We) (3) validated with a CMOS complementary LC-tank VCO. - At the fundamental frequency,(3)must hold This work was supported in part by the Shanghai Science& A=oC4+2c[n+4-u-)4-]}.④ Lo Technology Committee,P.R.China under System-Design-Chip (SDC)program (NO.037062019). Thus the effective capacitance Cemr is arrived 0-7803-8736-8/05/$20.00©2005IEEE. 687 ASP-DAC 2005
Abstract-This paper describes a new prediction method of tuning curves of a LC-tank voltage-controlled oscillator (VCO) with period calculation technique. With this period calculation technique, the prediction of oscillator tuning curves is more accurate compared with the traditional harmonic approxi -mation. The theoretical analyses are experimentally validated with a CMOS complementary LC-tank VCO implemented in 0.35µm 1P4M pure logic CMOS process. I. INTRODUCTION The complementary cross-coupled negative-Gm LC-tank oscillator is shown in Fig. 1, which employs both NMOS and PMOS cross-coupled pairs. Many published papers [1]-[4], have employed this type of LC-tank VCO, but oscillator tuning curves were obtained from SPICE simulations or measurements. The prediction of oscillator tuning curves is quite challenging due to highly nonlinear characteristics of varactors. A numerical method is shown in [2], but it is quite complex and time-consuming. The tuning curves must be numerically computed again if the bias current changes. M.Tiebout [3] and R.L.Bunch [4] et al. also found large-signal effects to the instantaneous capacitance of LC-tank, but their analyses were only qualitative. The recent papers in [5] and [6], introduced the notion of effective capacitance across the amplitude of oscillation, and presented an analytical solution to tank balance equation. Their approach was simple, but inaccurate since the second and higher order harmonics were neglected. Note that oscillating voltage in LC tank is not an ideal sinusoid [2], the effective capacitance of step-like varactors driven by a sinusoid is not the actual effective one in a true LC-tank VCO. Recently, the design and modeling of on-chip MOS varactors is a hot topic. However, these researches are focusing on how to implement MOS varactors with high quality and large tuning range on standard Silicon CMOS technology. Few of them deal with the large-signal analyses, nonlinear effect to C-V curves and tuning curves of LC-tank. In Section II, the harmonic approximation method of the large-signal nonlinearity of varactors is briefly recalled, and the effective capacitance of LC tank is calculated. Section III investigates I-V locus of step-like MOS varactors in a serial LC-tank and predicts the tuning curves through the calculation of oscillating period of a LC tank in time domain. In Section IV, our prediction method in time domain is compared with the harmonic approximation in frequency domain. Lastly, the theoretical analyses are experimentally validated with a CMOS complementary LC-tank VCO. This work was supported in part by the Shanghai Science & Technology Committee, P.R.China under System-Design-Chip (SDC) program (NO. 037062019). II. HARMONIC APPROXIMATION OF LC TANK IN FREQUENCY DOMAIN Traditional small-signal analysis is not suitable for LC-tank oscillators with large-amplitude swings [2-5]. The large-signal effect must be considered. Thus, the effective capacitance calculation of LC-tank circuit is not a simple time-average process. In this section, we will briefly present how to calculate the effective capacitance through large -signal nonlinear analysis of varactors in a serial LC-tank circuit [2],[4]-[6]. The presence of on-chip inductors in Fig. 1 imposes that the dc value of differential oscillating voltages has to be a constant voltage Vdc. Neglecting the tank losses in on-chip inductors and varactors, the half circuit of LC-tank VCO can be considered as a serial LC-tank structure (Fig. 2(a))[6]. The oscillating voltage waveform can be represented as a Fourier series: 0 ( ) 1 () 2 out n n V t V A cos n t ω ∞ = = + ∑ . (1) And, small-signal capacitance of varactors can be denoted as a Fourier series in time domain: () () ( ) 0 1 () 2 n ss C ss ss n C V C C cos n t ω ∞ = = + ∑ (2) where ( ) n Css is the Fourier coefficient at nth order harmonic. Since serial LC-tank circuits must satisfy the Kirchhoff’s laws, the inductor current must equal varactor current 1 () ( ) t C L C L ss C dV I I V t dt C V L dt −∞ =⇒ = ∫ . (3) At the fundamental frequency, (3) must hold () () () () 1 0 1 11 2 1 1 n ss ss n n n A CA C n A n A L ω ω ∞ + − = ⎧ ⎫ = + + −− ⎨ ⎡ ⎤ ⎣ ⎦⎬ ⎩ ⎭ ∑ . (4) Thus the effective capacitance Ceff is arrived Prediction of LC-VCOs’ Tuning Curves with Period Calculation Technique Zhangwen Tang, Jie He, Hongyan Jian, Haiqing Zhang, Jie Zhang, and Hao Min ASIC & System State Key Laboratory, Fudan University, Shanghai 200433, P.R.China Tel : +86-21-65642765*819 Fax : +86-21-65644158 E-mail : {zwtang, jiehe, hyjian, hmin}@fudan.edu.cn L0 =L C0=C Vctrl Mn1 Mn2 Mp1 Mp2 Mn5 Mn6 Mn3 Mn4 Bias-T Bias-T C3 C0=C L0=L Vdc Fig. 1. CMOS complementary cross-coupled LC-tank VCO 687 7D-6s 0-7803-8736-8/05/$20.00 ©2005 IEEE. ASP-DAC 2005
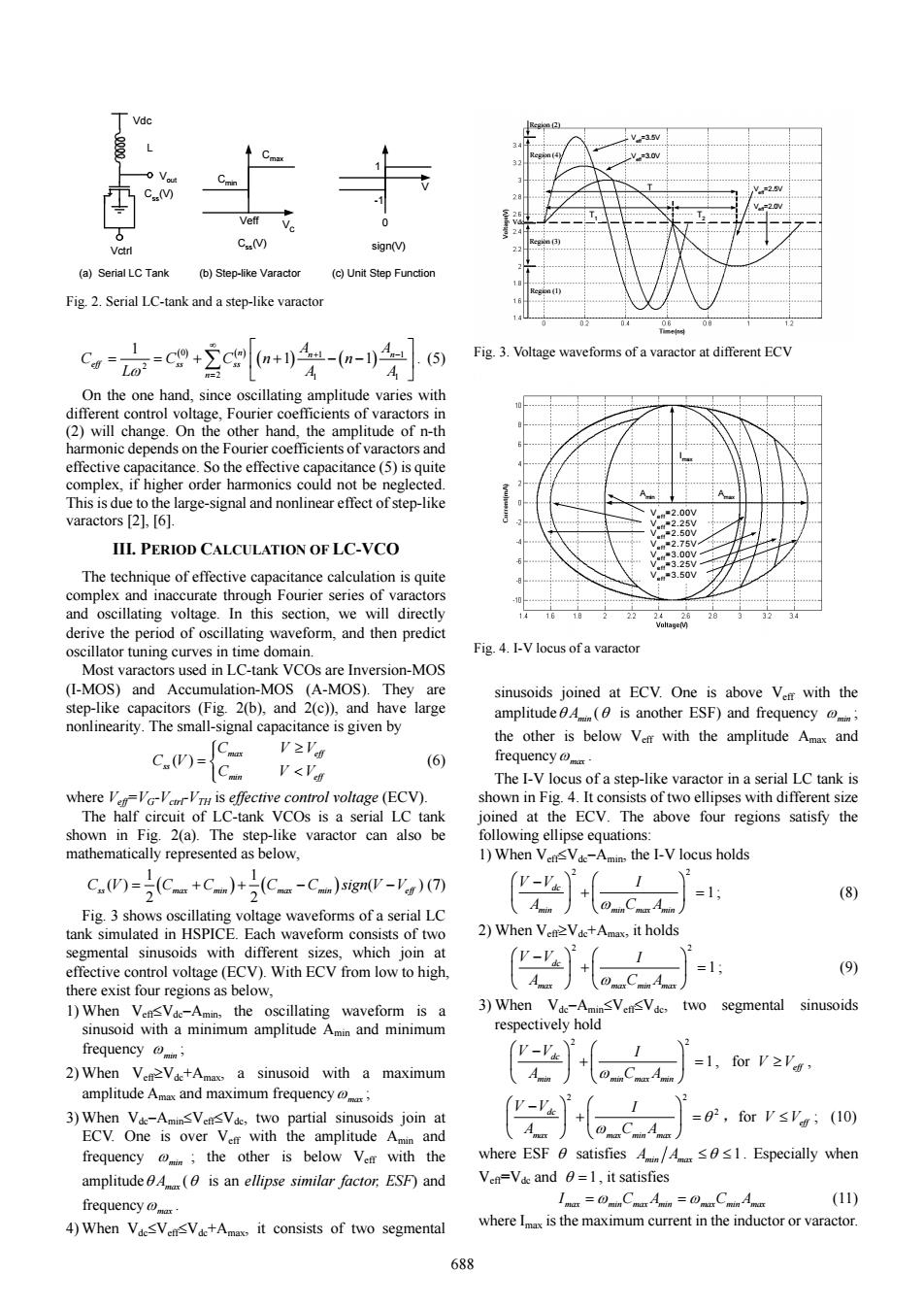
S 3v C.M Veff C.(V) Vctr sign(V) (a)Serial LC Tank (b)Step-like Varactor (c)Unit Step Function Fig.2.Serial LC-tank and a step-like varactor Fig.3.Voltage waveforms of a varactor at different ECV On the one hand,since oscillating amplitude varies with different control voltage,Fourier coefficients of varactors in (2)will change.On the other hand,the amplitude of n-th harmonic depends on the Fourier coefficients of varactors and effective capacitance.So the effective capacitance(5)is quite complex,if higher order harmonics could not be neglected. This is due to the large-signal and nonlinear effect of step-like varactors [2],[6]. V.=2.00V =2.25V IIL PERIOD CALCULATION OF LC-VCO 2.75 The technique of effective capacitance calculation is quite 3.50V complex and inaccurate through Fourier series of varactors and oscillating voltage.In this section,we will directly derive the period of oscillating waveform,and then predict oscillator tuning curves in time domain. Fig.4.I-V locus of a varactor Most varactors used in LC-tank VCOs are Inversion-MOS (I-MOS)and Accumulation-MOS (A-MOS).They are sinusoids joined at ECV.One is above Ver with the step-like capacitors (Fig.2(b),and 2(c)),and have large amplitude(is another ESF)and frequency nonlinearity.The small-signal capacitance is given by C.(W= (C V2Vn the other is below Verr with the amplitude Amax and V<Va (6) frequencym The I-V locus of a step-like varactor in a serial LC tank is where Ver=VG-Ver-Vr is effective control voltage (ECV). shown in Fig.4.It consists of two ellipses with different size The half circuit of LC-tank VCOs is a serial LC tank joined at the ECV.The above four regions satisfy the shown in Fig.2(a).The step-like varactor can also be following ellipse equations: mathematically represented as below, 1)When VensVde-Amin,the I-V locus holds C.)-i(C.+C.)+i(C-C)si@mv-Va)(1 =1 (8) Fig.3 shows oscillating voltage waveforms of a serial LC tank simulated in HSPICE.Each waveform consists of two 2)When Ven2Vde+Amax,it holds segmental sinusoids with different sizes,which join at effective control voltage(ECV).With ECV from low to high, j】 =1 (9) there exist four regions as below, 1)When VensVde-Amin,the oscillating waveform is a 3)When Vde-AminsVensVde,two segmental sinusoids sinusoid with a minimum amplitude Amin and minimum respectively hold frequency )2 =1, 2)When Ven2Vdc+Amax a sinusoid with a maximum for V2Vn, amplitude Amax and maximum frequency 2 3)When Vae-AminsVensVde,two partial sinusoids join at =82,forV≤'g;(10) ECV.One is over Ver with the amplitude Amin and frequency @the other is below Ver with the where ESF satisfies AA1.Especially when amplitude A is an ellipse similar factor.ESF)and Ven=Vdc and 0=1,it satisfies frequency Imax-0mar Amin-0mumin Am (11) 4)When VaesVensVde+Amax,it consists of two segmental where Imax is the maximum current in the inductor or varactor. 688
() () ( ) ( ) 0 1 1 2 2 1 1 1 1 1 n n n eff ss ss n A A C C Cn n Lω A A ∞ + − = ⎡ ⎤ = = + + −− ⎢ ⎥ ⎣ ⎦ ∑ . (5) On the one hand, since oscillating amplitude varies with different control voltage, Fourier coefficients of varactors in (2) will change. On the other hand, the amplitude of n-th harmonic depends on the Fourier coefficients of varactors and effective capacitance. So the effective capacitance (5) is quite complex, if higher order harmonics could not be neglected. This is due to the large-signal and nonlinear effect of step-like varactors [2], [6]. III. PERIOD CALCULATION OF LC-VCO The technique of effective capacitance calculation is quite complex and inaccurate through Fourier series of varactors and oscillating voltage. In this section, we will directly derive the period of oscillating waveform, and then predict oscillator tuning curves in time domain. Most varactors used in LC-tank VCOs are Inversion-MOS (I-MOS) and Accumulation-MOS (A-MOS). They are step-like capacitors (Fig. 2(b), and 2(c)), and have large nonlinearity. The small-signal capacitance is given by ( ) max eff ss min eff C VV C V C VV ⎧⎪ ≥ = ⎨ ⎪ < ⎩ (6) where Veff=VG-Vctrl-VTH is effective control voltage (ECV). The half circuit of LC-tank VCOs is a serial LC tank shown in Fig. 2(a). The step-like varactor can also be mathematically represented as below, ( ) ( ) 1 1 () ( ) 2 2 C V C C C C sign V V ss max min max min eff = ++ − − (7) Fig. 3 shows oscillating voltage waveforms of a serial LC tank simulated in HSPICE. Each waveform consists of two segmental sinusoids with different sizes, which join at effective control voltage (ECV). With ECV from low to high, there exist four regions as below, 1) When Veff≤Vdc−Amin, the oscillating waveform is a sinusoid with a minimum amplitude Amin and minimum frequency ω min ; 2) When Veff≥Vdc+Amax, a sinusoid with a maximum amplitude Amax and maximum frequencyω max ; 3) When Vdc−Amin≤Veff≤Vdc, two partial sinusoids join at ECV. One is over Veff with the amplitude Amin and frequency ω min ; the other is below Veff with the amplitudeθ Amax (θ is an ellipse similar factor, ESF) and frequencyω max . 4) When Vdc≤Veff≤Vdc+Amax, it consists of two segmental sinusoids joined at ECV. One is above Veff with the amplitudeθ Amin (θ is another ESF) and frequency ω min ; the other is below Veff with the amplitude Amax and frequencyω max . The I-V locus of a step-like varactor in a serial LC tank is shown in Fig. 4. It consists of two ellipses with different size joined at the ECV. The above four regions satisfy the following ellipse equations: 1) When Veff≤Vdc−Amin, the I-V locus holds 2 2 1 dc min min max min V V I A CA ω ⎛ ⎞⎛ ⎞ − ⎜ ⎟⎜ ⎟ + = ⎝ ⎠⎝ ⎠ ; (8) 2) When Veff≥Vdc+Amax, it holds 2 2 1 dc max max min max V V I A CA ω ⎛ ⎞⎛ ⎞ − ⎜ ⎟⎜ ⎟ + = ⎝ ⎠⎝ ⎠ ; (9) 3) When Vdc−Amin≤Veff≤Vdc, two segmental sinusoids respectively hold 2 2 1 dc min min max min V V I A CA ω ⎛ ⎞⎛ ⎞ − ⎜ ⎟⎜ ⎟ + = ⎝ ⎠⎝ ⎠ , for V V≥ eff , 2 2 dc 2 max max min max V V I A CA θ ω ⎛ ⎞⎛ ⎞ − ⎜ ⎟⎜ ⎟ + = ⎝ ⎠⎝ ⎠ ,for V V≤ eff ; (10) where ESF θ satisfies 1 A A min max ≤ ≤ θ . Especially when Veff=Vdc and θ = 1, it satisfies max min max min max min max I =ω CA CA =ω (11) where Imax is the maximum current in the inductor or varactor. L Css(V) Vdc Vctrl Cmax Cmin VC 1 -1 0 V Css(V) sign(V) (a) Serial LC Tank (b) Step-like Varactor (c) Unit Step Function Vout Veff Fig. 2. Serial LC-tank and a step-like varactor Vdc Region (2) Region (4) Region (3) Region (1) Veff=3.5V Veff=3.0V Veff=2.0V Veff=2.5V T2 T1 T Fig. 3. Voltage waveforms of a varactor at different ECV Veff=2.00V Veff=2.25V Veff=2.50V Veff=2.75V Veff=3.00V Veff=3.25V Veff=3.50V Amin Amax I max Fig. 4. I-V locus of a varactor 688
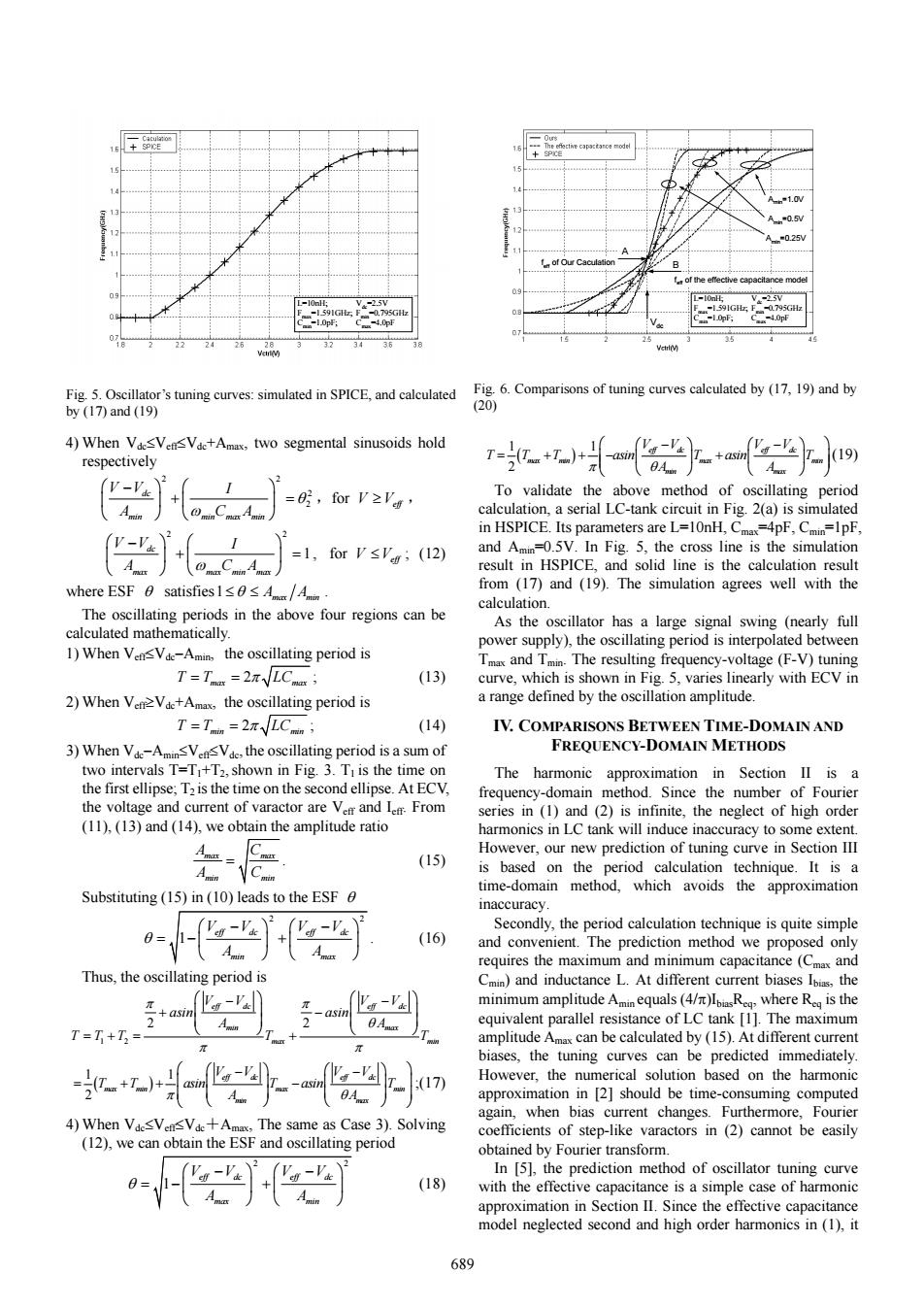
=0.5 ■0.25 of Our Caculatic .of the e L-1OpH: -10am 2 1591Gz 0.795GHz -10pF: C-4.0pF -4.0pF 34 36 Fig.5.Oscillator's tuning curves:simulated in SPICE,and calculated Fig.6.Comparisons of tuning curves calculated by (17,19)and by by(17)and(19) (20) 4)When VaesVensVde+Amax,two segmental sinusoids hold respectively r{am-小 =e,forV≥'t To validate the above method of oscillating period calculation,a serial LC-tank circuit in Fig.2(a)is simulated in HSPICE.Its parameters are L=10nH,Cma=4pF,Cmin=1pF. =1. forV≤'g;(l2) and Amin=0.5V.In Fig.5,the cross line is the simulation result in HSPICE,and solid line is the calculation result where ESF0 satisfies1≤B≤Ama/An from (17)and (19).The simulation agrees well with the calculation. The oscillating periods in the above four regions can be As the oscillator has a large signal swing (nearly full calculated mathematically. power supply),the oscillating period is interpolated between 1)When VenVde-Amin,the oscillating period is Tmax and Tmin.The resulting frequency-voltage (F-V)tuning T=Tnax=2π√LC (13) curve,which is shown in Fig.5,varies linearly with ECV in 2)When VenVde+Amax,the oscillating period is a range defined by the oscillation amplitude T=Tn=2π√LCn; (14) IV.COMPARISONS BETWEEN TIME-DOMAIN AND 3)When Vde-AminsVensVde,the oscillating period is a sum of FREQUENCY-DOMAIN METHODS two intervals T=T +T2,shown in Fig.3.TI is the time on The harmonic approximation in Section II is a the first ellipse;T2 is the time on the second ellipse.At ECV, frequency-domain method.Since the number of Fourier the voltage and current of varactor are Ver and Ie From series in (1)and(2)is infinite,the neglect of high order (11),(13)and(14),we obtain the amplitude ratio harmonics in LC tank will induce inaccuracy to some extent. 先 However,our new prediction of tuning curve in Section III (15) is based on the period calculation technique.It is a time-domain method,which avoids the approximation Substituting(15)in(10)leads to the ESF inaccuracy. Secondly,the period calculation technique is quite simple + (16) and convenient.The prediction method we proposed only requires the maximum and minimum capacitance (Cmax and Thus,the oscillating period is Cmin)and inductance L.At different current biases Ipias,the minimum amplitude Aminequals(4/)IpR where R is the equivalent parallel resistance of LC tank [1].The maximum T=T+T= amplitude Amax can be calculated by (15).At different current biases,the tuning curves can be predicted immediately. 女e-uw However,the numerical solution based on the harmonic approximation in [2]should be time-consuming computed again,when bias current changes.Furthermore,Fourier 4)When VaesVensVde+Amax,The same as Case 3).Solving coefficients of step-like varactors in (2)cannot be easily (12),we can obtain the ESF and oscillating period obtained by Fourier transform. -) In [5],the prediction method of oscillator tuning curve (18) with the effective capacitance is a simple case of harmonic approximation in Section II.Since the effective capacitance model neglected second and high order harmonics in (1),it 689
4) When Vdc≤Veff≤Vdc+Amax, two segmental sinusoids hold respectively 2 2 2 2 dc min min max min V V I A CA θ ω ⎛ ⎞⎛ ⎞ − ⎜ ⎟⎜ ⎟ + = ⎝ ⎠⎝ ⎠ ,for V V≥ eff , 2 2 1 dc max max min max V V I A CA ω ⎛ ⎞⎛ ⎞ − ⎜ ⎟⎜ ⎟ + = ⎝ ⎠⎝ ⎠ , for V V≤ eff ; (12) where ESF θ satisfies1 ≤ ≤ θ Amax min A . The oscillating periods in the above four regions can be calculated mathematically. 1) When Veff≤Vdc−Amin, the oscillating period is 2 T T LC = = max max π ; (13) 2) When Veff≥Vdc+Amax, the oscillating period is 2 T T LC = = min min π ; (14) 3) When Vdc−Amin≤Veff≤Vdc, the oscillating period is a sum of two intervals T=T1+T2,shown in Fig. 3. T1 is the time on the first ellipse; T2 is the time on the second ellipse. At ECV, the voltage and current of varactor are Veff and Ieff. From (11), (13) and (14), we obtain the amplitude ratio max max min min A C A C = . (15) Substituting (15) in (10) leads to the ESF θ 2 2 1 eff dc eff dc min max VV VV A A θ ⎛ ⎞⎛ ⎞ − − =− + ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ . (16) Thus, the oscillating period is 1 2 2 2 eff dc eff dc min max max min VV VV asin asin A A TTT T T π π θ π π ⎛⎞ ⎛⎞ − − + − ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ =+ = + ( ) 1 1 2 eff dc eff dc max min max min min max VV VV T T asin T asin T π θ A A ⎛ ⎞ ⎛⎞ ⎛⎞ − − = ++ − ⎜ ⎟ ⎜⎟ ⎜⎟ ⎝ ⎠ ⎝⎠ ⎝⎠ ;(17) 4) When Vdc≤Veff≤Vdc+Amax, The same as Case 3). Solving (12), we can obtain the ESF and oscillating period 2 2 1 eff dc eff dc max min VV VV A A θ ⎛ ⎞⎛ ⎞ − − =− + ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ (18) ( ) 1 1 2 eff dc eff dc max min max min min max VV VV T T T asin T asin T π θA A ⎛ ⎞ ⎛⎞ ⎛⎞ − − = + +− + ⎜ ⎟ ⎜⎟ ⎜⎟ ⎝ ⎠ ⎝⎠ ⎝⎠ (19) To validate the above method of oscillating period calculation, a serial LC-tank circuit in Fig. 2(a) is simulated in HSPICE. Its parameters are L=10nH, Cmax=4pF, Cmin=1pF, and Amin=0.5V. In Fig. 5, the cross line is the simulation result in HSPICE, and solid line is the calculation result from (17) and (19). The simulation agrees well with the calculation. As the oscillator has a large signal swing (nearly full power supply), the oscillating period is interpolated between Tmax and Tmin. The resulting frequency-voltage (F-V) tuning curve, which is shown in Fig. 5, varies linearly with ECV in a range defined by the oscillation amplitude. IV. COMPARISONS BETWEEN TIME-DOMAIN AND FREQUENCY-DOMAIN METHODS The harmonic approximation in Section II is a frequency-domain method. Since the number of Fourier series in (1) and (2) is infinite, the neglect of high order harmonics in LC tank will induce inaccuracy to some extent. However, our new prediction of tuning curve in Section III is based on the period calculation technique. It is a time-domain method, which avoids the approximation inaccuracy. Secondly, the period calculation technique is quite simple and convenient. The prediction method we proposed only requires the maximum and minimum capacitance (Cmax and Cmin) and inductance L. At different current biases Ibias, the minimum amplitude Amin equals (4/π)IbiasReq, where Req is the equivalent parallel resistance of LC tank [1]. The maximum amplitude Amax can be calculated by (15). At different current biases, the tuning curves can be predicted immediately. However, the numerical solution based on the harmonic approximation in [2] should be time-consuming computed again, when bias current changes. Furthermore, Fourier coefficients of step-like varactors in (2) cannot be easily obtained by Fourier transform. In [5], the prediction method of oscillator tuning curve with the effective capacitance is a simple case of harmonic approximation in Section II. Since the effective capacitance model neglected second and high order harmonics in (1), it L=10nH; Vdc=2.5V Fmax=1.591GHz; Fmin=0.795GHz Cmin=1.0pF; Cmax=4.0pF Fig. 5. Oscillator’s tuning curves: simulated in SPICE, and calculated by (17) and (19) L=10nH; Vdc=2.5V Fmax=1.591GHz; Fmin=0.795GHz Cmin=1.0pF; Cmax=4.0pF Amin=1.0V Amin=0.5V Amin=0.25V f eff of Our Caculation A f eff of the effective capacitance model B Vdc Fig. 6. Comparisons of tuning curves calculated by (17, 19) and by (20) 689
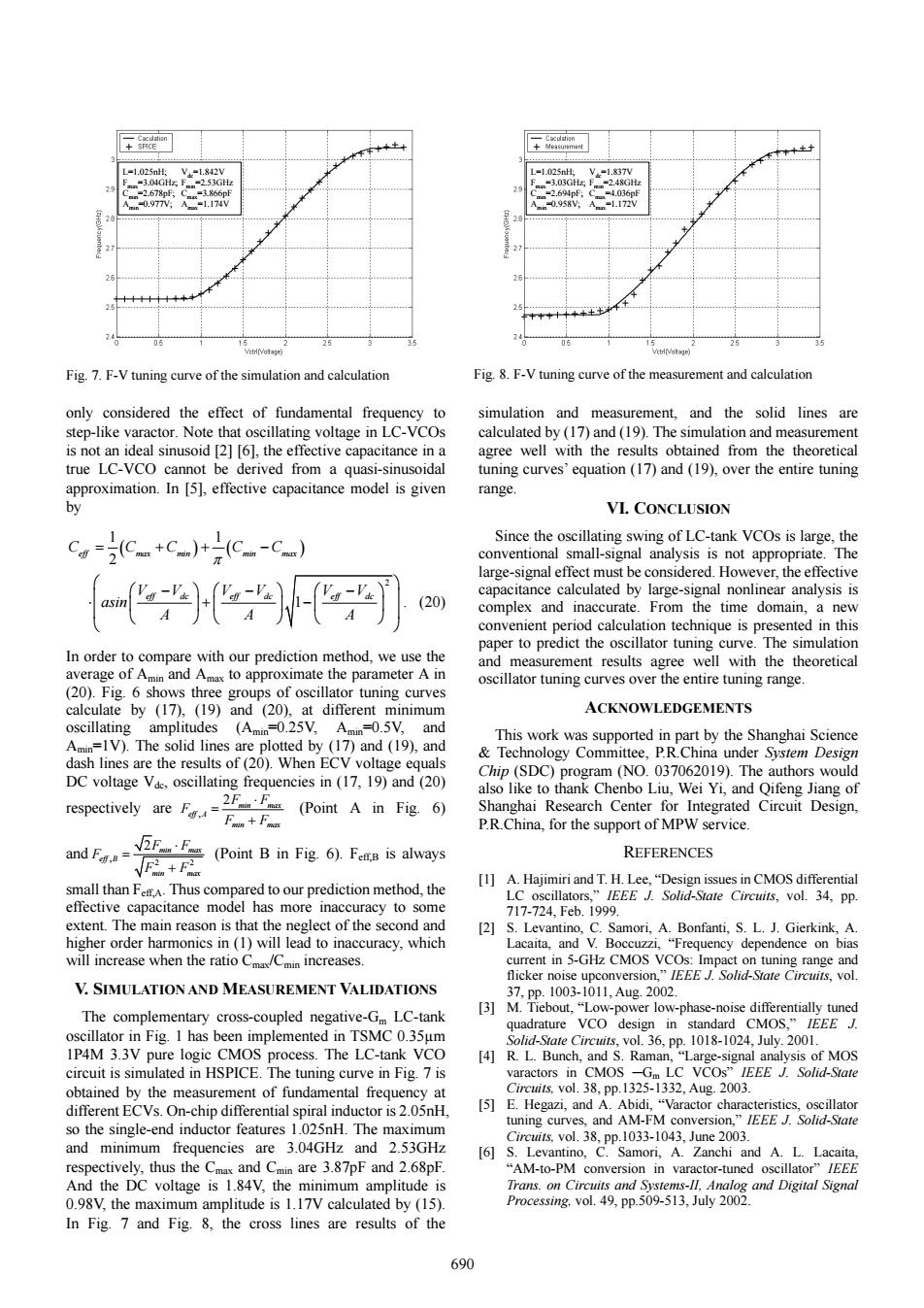
=1025nH V-1.842V V-l.837V -253GH -3.03GH 248GH -2.678pf =主g66 -2.694pF -4.036p .0.977 A-1.174V 0.958: .172V <5 Fig.7.F-V tuning curve of the simulation and calculation Fig.8.F-V tuning curve of the measurement and calculation only considered the effect of fundamental frequency to simulation and measurement.and the solid lines are step-like varactor.Note that oscillating voltage in LC-VCOs calculated by(17)and(19).The simulation and measurement is not an ideal sinusoid [2][6],the effective capacitance in a agree well with the results obtained from the theoretical true LC-VCO cannot be derived from a quasi-sinusoidal tuning curves'equation(17)and(19),over the entire tuning approximation.In [5],effective capacitance model is given range. y VI.CONCLUSION Cw=2(Cm+C)+-(C-C) Since the oscillating swing of LC-tank VCOs is large,the conventional small-signal analysis is not appropriate.The large-signal effect must be considered.However,the effective capacitance calculated by large-signal nonlinear analysis is (20) complex and inaccurate.From the time domain,a new convenient period calculation technique is presented in this paper to predict the oscillator tuning curve.The simulation In order to compare with our prediction method,we use the and measurement results agree well with the theoretical average of Amin and Amax to approximate the parameter A in oscillator tuning curves over the entire tuning range. (20).Fig.6 shows three groups of oscillator tuning curves calculate by (17),(19)and (20),at different minimum ACKNOWLEDGEMENTS oscillating amplitudes (Amin=0.25V,Amin=0.5V,and This work was supported in part by the Shanghai Science Amin=1V).The solid lines are plotted by (17)and (19),and Technology Committee,P.R.China under System Design dash lines are the results of(20).When ECV voltage equals DC voltage Vde,oscillating frequencies in(17,19)and(20) Chip(SDC)program (NO.037062019).The authors would also like to thank Chenbo Liu,Wei Yi,and Qifeng Jiang of respectively areF(Point A in Fig.6) Shanghai Research Center for Integrated Circuit Design, P.R.China,for the support of MPW service and F.= (Point B in Fig.6).Fes is always REFERENCES [1]A.Hajimiri and T.H.Lee,"Design issues in CMOS differential small than FeA.Thus compared to our prediction method,the effective capacitance model has more inaccuracy to some LC oscillators,"IEEE J.Solid-State Circuits,vol.34,pp. 717-724,Feb.1999. extent.The main reason is that the neglect of the second and [2]S.Levantino,C.Samori,A.Bonfanti,S.L.J.Gierkink,A. higher order harmonics in (1)will lead to inaccuracy,which Lacaita,and V.Boccuzzi,"Frequency dependence on bias will increase when the ratio Cma/Cmin increases. current in 5-GHz CMOS VCOs:Impact on tuning range and flicker noise upconversion,"IEEE J.Solid-State Circuits,vol. V.SIMULATION AND MEASUREMENT VALIDATIONS 37.pp.1003-1011,Aug.2002. The complementary cross-coupled negative-Gm LC-tank [3]M.Tiebout,"Low-power low-phase-noise differentially tuned quadrature VCO design in standard CMOS,"IEEE J. oscillator in Fig.I has been implemented in TSMC 0.35um Solid-State Circuits,vol.36,pp.1018-1024,July.2001. 1P4M 3.3V pure logic CMOS process.The LC-tank VCO [4]R.L.Bunch,and S.Raman,"Large-signal analysis of MOS circuit is simulated in HSPICE.The tuning curve in Fig.7 is varactors in CMOS -Gm LC VCOs"IEEE J.Solid-State obtained by the measurement of fundamental frequency at Circuits,vol.38,pp.1325-1332,Aug.2003. different ECVs.On-chip differential spiral inductor is 2.05nH. [5] E.Hegazi,and A.Abidi,"Varactor characteristics,oscillator so the single-end inductor features 1.025nH.The maximum tuning curves,and AM-FM conversion,"IEEE J.Solid-State and minimum frequencies are 3.04GHz and 2.53GHz Circuits,vol.38,pp.1033-1043,June 2003. [6]S.Levantino,C.Samori,A.Zanchi and A.L.Lacaita respectively,thus the Cmax and Cmin are 3.87pF and 2.68pF. "AM-to-PM conversion in varactor-tuned oscillator"/EEE And the DC voltage is 1.84V,the minimum amplitude is Trans.on Circuits and Systems-II,Analog and Digital Signal 0.98V,the maximum amplitude is 1.17V calculated by (15). Processing.vol.49,pp.509-513,July 2002. In Fig.7 and Fig.8,the cross lines are results of the 690
only considered the effect of fundamental frequency to step-like varactor. Note that oscillating voltage in LC-VCOs is not an ideal sinusoid [2] [6], the effective capacitance in a true LC-VCO cannot be derived from a quasi-sinusoidal approximation. In [5], effective capacitance model is given by ( ) ( ) 1 1 2 C CC CC eff max min min max π = ++ − 2 1 VV VV VV eff dc eff dc eff dc asin AA A ⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎛ ⎞ −− − ⎜ ⎟ ⋅ +− ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠ ⎝ ⎠ . (20) In order to compare with our prediction method, we use the average of Amin and Amax to approximate the parameter A in (20). Fig. 6 shows three groups of oscillator tuning curves calculate by (17), (19) and (20), at different minimum oscillating amplitudes (Amin=0.25V, Amin=0.5V, and Amin=1V). The solid lines are plotted by (17) and (19), and dash lines are the results of (20). When ECV voltage equals DC voltage Vdc, oscillating frequencies in (17, 19) and (20) respectively are , 2 min max eff A min max F F F F F ⋅ = + (Point A in Fig. 6) and , 2 2 2 min max eff B min max F F F F F ⋅ = + (Point B in Fig. 6). Feff,B is always small than Feff,A. Thus compared to our prediction method, the effective capacitance model has more inaccuracy to some extent. The main reason is that the neglect of the second and higher order harmonics in (1) will lead to inaccuracy, which will increase when the ratio Cmax/Cmin increases. V. SIMULATION AND MEASUREMENT VALIDATIONS The complementary cross-coupled negative-Gm LC-tank oscillator in Fig. 1 has been implemented in TSMC 0.35µm 1P4M 3.3V pure logic CMOS process. The LC-tank VCO circuit is simulated in HSPICE. The tuning curve in Fig. 7 is obtained by the measurement of fundamental frequency at different ECVs. On-chip differential spiral inductor is 2.05nH, so the single-end inductor features 1.025nH. The maximum and minimum frequencies are 3.04GHz and 2.53GHz respectively, thus the Cmax and Cmin are 3.87pF and 2.68pF. And the DC voltage is 1.84V, the minimum amplitude is 0.98V, the maximum amplitude is 1.17V calculated by (15). In Fig. 7 and Fig. 8, the cross lines are results of the simulation and measurement, and the solid lines are calculated by (17) and (19). The simulation and measurement agree well with the results obtained from the theoretical tuning curves’ equation (17) and (19), over the entire tuning range. VI. CONCLUSION Since the oscillating swing of LC-tank VCOs is large, the conventional small-signal analysis is not appropriate. The large-signal effect must be considered. However, the effective capacitance calculated by large-signal nonlinear analysis is complex and inaccurate. From the time domain, a new convenient period calculation technique is presented in this paper to predict the oscillator tuning curve. The simulation and measurement results agree well with the theoretical oscillator tuning curves over the entire tuning range. ACKNOWLEDGEMENTS This work was supported in part by the Shanghai Science & Technology Committee, P.R.China under System Design Chip (SDC) program (NO. 037062019). The authors would also like to thank Chenbo Liu, Wei Yi, and Qifeng Jiang of Shanghai Research Center for Integrated Circuit Design, P.R.China, for the support of MPW service. REFERENCES [1] A. Hajimiri and T. H. Lee, “Design issues in CMOS differential LC oscillators,” IEEE J. Solid-State Circuits, vol. 34, pp. 717-724, Feb. 1999. [2] S. Levantino, C. Samori, A. Bonfanti, S. L. J. Gierkink, A. Lacaita, and V. Boccuzzi, “Frequency dependence on bias current in 5-GHz CMOS VCOs: Impact on tuning range and flicker noise upconversion,” IEEE J. Solid-State Circuits, vol. 37, pp. 1003-1011, Aug. 2002. [3] M. Tiebout, “Low-power low-phase-noise differentially tuned quadrature VCO design in standard CMOS,” IEEE J. Solid-State Circuits, vol. 36, pp. 1018-1024, July. 2001. [4] R. L. Bunch, and S. Raman, “Large-signal analysis of MOS varactors in CMOS ─Gm LC VCOs” IEEE J. Solid-State Circuits, vol. 38, pp.1325-1332, Aug. 2003. [5] E. Hegazi, and A. Abidi, “Varactor characteristics, oscillator tuning curves, and AM-FM conversion,” IEEE J. Solid-State Circuits, vol. 38, pp.1033-1043, June 2003. [6] S. Levantino, C. Samori, A. Zanchi and A. L. Lacaita, “AM-to-PM conversion in varactor-tuned oscillator” IEEE Trans. on Circuits and Systems-II, Analog and Digital Signal Processing, vol. 49, pp.509-513, July 2002. L=1.025nH; Vdc=1.837V Fmax=3.03GHz; Fmin=2.48GHz Cmin=2.694pF; Cmax=4.036pF Amin=0.958V; Amax=1.172V Fig. 8. F-V tuning curve of the measurement and calculation L=1.025nH; Vdc=1.842V Fmax=3.04GHz; Fmin=2.53GHz Cmin=2.678pF; Cmax=3.866pF Amin=0.977V; Amax=1.174V Fig. 7. F-V tuning curve of the simulation and calculation 690