
第三章向量空间与线性方程组解的结构题库 一、选择是 1.已知向量2a+0=L.-2.-2)了.3a+2B=0-4.-3),则a+B-〔)(中等) A(0-2,-1 R.(-2.0.-107 C(1.-l.-2) 0.(2-6,-5 2.设可由向量g-(0,2,0,G一@,0,1Y找性表示,则下列向量中B只能是()(中等) A(2,2.1 B.(-3.0.2y c.L.1.0 D.0,4,5) 3设白量云(-23订,运-21y,G67y,则向量a可由()性表示(中等) A.a -2a B4+4a C.-a +2a D.-a+4a 4,向量组G…2,的秩不为s(g之2)的充要条件是()(较易) A.马风…区,全是非零向量 B。么鸡《,全是零向量 C。马4…区,中至少有一个向量可由其它向量线性表示 D。马码a,中至少有一个零向量 五,设A是n阶方阵,且A的第一行可由其余刀一1个行向量线性表示,则下列结论中情误的 是()(中等) A.B(A)S n-1 BA有一个列向量可由其会列向量线性表示 C.H=0 D.A的m-1阶余子式全为零 丘设出,L,比为n推向量,下列结论正确的是()(做南) u A.若kg+k4+L+k。=0,则a,a,L,a线性相关 且.若任意一组不全为零的数k,六,…,k,有k区+ka+L+k区。0 则么,4L,位.线性无关 C.若a,色,L,a,线性相关。则对任何一组不全为零的数太人L,k有 kg+k%+L+k区=0
第三章 向量空间与线性方程组解的结构题库 一、选择题 1.已知向量 2 (1, 2, 2) ,3 2 (1, 4, 3) T T + = − − + = − − ,则 + = ( )(中等) A. (0, 2, 1)T − − B. ( 2,0, 1)T − − C. (1, 1, 2)T − − D. (2, 6, 5)T − − 2.设 可由向量 1 2 = ,2,0 , = 0,0,1 T T (0 ) ( ) 线性表示,则下列向量中 只能是( )(中等) A. (2,2,1)T B. ( 3,0,2)T − C. (1,1,0)T D. (0,4,5)T 3.设向量 1 2 3 = 2 3 , = 2 1 , = 6 7 T T T (− ) ( ) ( ) ,则向量 3 可由( )线性表示(中等) A. 1 2 − 2 B. 1 2 + 4 C. 1 2 − + 2 D. 1 2 − + 4 4.向量组 1 2 ,, ,s, 的秩不为 s( ( 2) s 的充要条件是( )(较易) A. 1 2 ,, ,s, 全是非零向量 B. 1 2 ,, ,s, 全是零向量 C. 1 2 ,, ,s, 中至少有一个向量可由其它向量线性表示 D. 1 2 ,, ,s, 中至少有一个零向量 5.设 A 是 n 阶方阵,且 A 的第一行可由其余 n−1 个行向量线性表示,则下列结论中错误的 是( )(中等) A. R A n ( ) 1 − B. A 有一个列向量可由其余列向量线性表示 C. ||0 A = D. A 的 n −1 阶余子式全为零 6. 设 1 2 , , , m uur uur uur L 为 n 维向量,下列结论正确的是( ) (较难) A.若 1 1 2 2 0 m m k k k + + + = uur uur uur L ,则 1 2 , , , m uur uur uur L 线性相关 B.若任意一组不全为零的数 1 2 , , , m k k k ,有 1 1 2 2 0 m m k k k + + + uur uur uur L , 则 1 2 , , , m uur uur uur L 线性无关 C.若 1 2 , , , m uur uur uur L 线性相关,则对任何一组不全为零的数 1 2 , , , m k k k L 有 1 1 2 2 0 m m k k k + + + = uur uur uur L

D.着0成+0+L.+0成-0,则,品L,线性相关 7,已知,丝找性无关。以下线性无关的是()(中等) Agt%高+乌乌-马 B.%+%馬+%%+2%+% Ca+2a24+3gg+34D.g+4+g2a-3g+%3g-2a+3g 8设向量组a马及,的肤为r B.02k C.R(A)k D.R(A)S 14,设A是矩阵,则齐次网x用线性方程组X=0仅有零解的充分必要条件() A,A的列向量线性无关 B。A的列向量线性相关 C.A的行向量线性无关 D。A的行向量线性相关 15,设向量组A:风,,.C4与向量组B:民,民,月等价,则(》(中等)
D.若 1 2 0 0 0 0 + + + = m uur uur uur L ,则 1 2 , , , m uur uur uur L 线性相关 7.已知 1 2 3 ,, 线性无关,以下线性无关的是( )(中等) A. 1 2 2 3 3 1 + + − B. 1 2 2 3 1 2 3 + + + + 2 C. 1 2 2 3 1 3 + 2 2 3 3 + + D. 1 2 3 1 2 3 1 2 3 + + − + − + 2 3 3 2 3 8.设向量组 1 2 ,, ,s 的秩为 r r s ( ) ,则向量组 1 2 ,, ,s, 中( ) A.多于 r 个向量的部分组必线性无关 B.多于 r 个向量的部分组必线性相关 C.少于 r 个向量的部分组必线性无关 D.少于 r 个向量的部分组必线性相关 9.设向量 , , 线性无关, , , 线性相关,下列( )成立 A. 必可由 , , 线性表示 B. 必不可由 , , 线性表示 C. 必可由 , , 线性表示 D. 必不可由 , , 线性表示 10.一个向量组中的极大线性无关组( ) A.唯一 B.个数唯一 C. 所含向量个数唯一 D.所含向量个数不唯一 11.设矩阵 ( 1 2 3 4 ) 1 0 0 5 0 1 0 7 , 0 0 1 3 0 0 0 0 A = = , , 则( )不是向量组 1 2 3 4 ,, , 的一个极 大无关组.(较易) A. 2 3 4 , ,, B. 1 2 3 , , C. 1 2 4 ,, D. 1 2 3 4 ,,, 12.设向量组 A : 1 2 3 4 ,, , 是一组 n 维向量,且 1 2 3 , , 线性相关,则( ) A. 4 RA = B. R n A = C. 1 RA = D. 3 RA 13.已知 A 的一个 k 阶子式不等于 0,则 R A( ) 满足( ) A. R A k ( ) B. R A k ( ) C. R A k ( )= D. R A k ( ) 14.设 A 是矩阵,则齐次 m n 线性方程组 AX = 0 仅有零解的充分必要条件( ) A. A 的列向量线性无关 B. A 的列向量线性相关 C. A 的行向量线性无关 D. A 的行向量线性相关 15.设向量组 A : 1 2 3 4 , , , 与向量组 B : 1 2 3 , , 等价,则( )(中等)

A,向量组A线性无关 B。向量组B线性无关 C。向量组A线性相美 D。向量组B线性相美 16.设AB为同阶方阵且R(A)=RB),则必有() AIAHBI BA与B相同 C.A与B等价 D.A=B 17.已知AB=C且B任0,则下列说法正确的是() A矩阵C的列向量与矩阵A的列向量等价 B。矩阵C的行向量与矩阵A的行向量等价 C。矩阵C的列向量与矩阵B的列向量等价 D.矩阵C的行向量与矩阵B的行向量等价 2与-马+马=0 18,设齐次线性方程组 名一马2一马■0有非零解,则无为()(中等) 年++=0 A.=1 B.0 C.1 D.2 属+无+马=4 19.已知线性方程组 无+此+x=3无解,则数a=()《中等) 2x+22=4 B.0 D.1 20.要使写- 都是线性方程组Ax■0的解,只要系数矩阵A=()(中等) 2 01 A(-2,1) 20 -102 4-2-2 011 012 011 无+252+33=0 21.齐次线性方程组 的基础解系所含解向量的个数为()(较易) 号-不3+无=0 A.1 B.2 C,3 0.4 22.已知功是套齐次线性方程组Ax=万的解,三是A任=0的解,则下列结论正确的是() (较易) A.5+刀是A红=0的解 B专-7是在=6的解
A.向量组 A 线性无关 B.向量组 B 线性无关 C.向量组 A 线性相关 D.向量组 B 线性相关 16.设 A B 、 为同阶方阵且 R A R B ( ) ( ) = ,则必有( ) A. | | | | A B = B. A 与 B 相同 C. A 与 B 等价 D. A B = 17.已知 AB C= 且 | | 0 B ,则下列说法正确的是( ) A. 矩阵 C 的列向量与矩阵 A 的列向量等价 B.矩阵 C 的行向量与矩阵 A 的行向量等价 C.矩阵 C 的列向量与矩阵 B 的列向量等价 D.矩阵 C 的行向量与矩阵 B 的行向量等价 18.设齐次线性方程组 + + = − − = − + = 0 0 2 0 1 2 3 1 2 3 1 2 3 x x x x x x x x x 有非零解,则 为( )(中等) A.-1 B.0 C.1 D.2 19.已知线性方程组 1 2 3 1 2 3 1 2 4 3 2 2 4 x x x x ax x x ax + + = + + = + = 无解,则数 a = ( )(中等) A. 1 2 − B. 0 C. 1 2 D. 1 20.要使 1 2 1 0 0 , 1 2 1 = = − 都是线性方程组 Ax = 0 的解,只要系数矩阵 A = ( )(中等) A. (−2,1,1) B. 2 0 1 0 1 1 − C. 1 0 2 0 1 2 − D. 0 1 1 422 0 1 1 − − − 21.齐次线性方程组 1 2 3 2 3 4 2 3 0 0 x x x x x x + + = − + = 的基础解系所含解向量的个数为( )(较易) A.1 B.2 C.3 D.4 22.已知 r 是非齐次线性方程组 Ax b = 的解, r 是 Ax = 0 的解,则下列结论正确的是( ) (较易) A. + r r 是 Ax = 0 的解 B. − r r 是 Ax b = 的解

41 C.5+n是A标=石的解 D.-7是在=0的解 23设A是4×3知阵,4)=L司,员,司是丰齐次找性方程组在=6的三个找性无关解, 下列《 )是Ax=0的基础解系。(较难) 人哥+易+写 B.孟+-2写 0.6--哥 D.+6品+写 24.设A是5×4矩阵,网)=2,云,石是非齐次线性方程组A=万的两个解,云是G=司 的一个解,则()为A红=乃的解。 A.+品+写 B+员-2写 c.哥-写 D写- 25.设A是m×H矩库,则齐次找性方程组AX=0有零解的充要条件是()(中等) A.=n且R(A)=H B.m)n C.R(A)= D方程组AX=B有唯一解 6,设A是m×:矩库,则非齐次线性方程组A=B有无穷多解的充要条件是《 (中等) A.R(A)(n 且.R(A)m C.m(a D.m(n且R()m 二、填空圈 27.设a=2,-3,50=1,7,2则2a-B 一(较易) 28.设a-(L2,-3y0-(3.-2.1,则a+2B (较号) 29设向量a-(6-2,0.4)},=(-3.157),若向量7满足2a+7-30 则7 (较易) 30.秩相等是相同维数向量组等价的 条件.(中等) 31, 已知向量组A:网 区3■ 和B:A 2 则向量组A与向量组B的关系为 (中等)
C. + r r 是 Ax b = 的解 D. − r r 是 Ax = 0 的解 23.设 A 是 4 3 矩阵, R A( ) 1, = 1 2 3 , , 是非齐次线性方程组 Ax b = 的三个线性无关解, 下列( )是 Ax = 0 的基础解系。(较难) A. 1 2 3 + + B. 1 2 3 + −2 C. 2 1 3 2 − − , D. 1 2 2 3 + + , 24.设 A 是 5 4 矩阵, R A( ) 2, = 1 2 , 是非齐次线性方程组 Ax b = 的两个解, 3 是 Ax = 0 的一个解,则( )为 Ax b = 的解。 A. 1 2 3 + + B. 1 2 3 + −2 C. 2 3 − D. 3 1 − 25.设 A 是 mn 矩阵,则齐次线性方程组 AX = 0 有零解的充要条件是( )(中等) A. m=n 且 R A n ( ) = B. mn C. R A n ( ) = D.方程组 AX B = 有唯一解 26.设 A 是 mn 矩阵,则非齐次线性方程组 AX B = 有无穷多解的充要条件是( ) (中等) A. R A n ( ) B. R A( )m C.mn D.mn 且 R A( )=m 二、填空题 27.设 ( ) ( ) T T = 2,-3,5 ,= 1,7,-2 ur ur 则 2 − = .(较易) 28.设 (1 3) (3 ) T T = ,2,- ,= ,-2,1 , 则 + = 2 ur ur .(较易) 29.设向量 (6, 2,0,4) ( 3,1,5,7) T T = − ,= − , 若向量 满足 2 3 + = 则 = r . (较易) 30.秩相等是相同维数向量组等价的 条件.(中等) 31. 1 2 1 2 3 1 2 4 1 2 : 0 , 1 , : 1 , 2 , 5 2 5 3 1 3 B − − = = = − = = 已知向量组A 和 ur uur u uur uur uur 则向量组A与向量组B的关系为 .(中等)

100 32.设三阶矩阵A= 20则矩阵A的秩为 (较易) 333 113 33.设三阶矩阵A= 125 则矩阵A的铁为 (较易) 339 123 34.设三阶矩阵A= 235 则矩库A的供为 (较易) (347 12 1 2-2 35设A= 2 已知(0=2,则:= (中等) -11 6 1 0-3 6,已知向量组向量G,庄于找性相关。而豆入,石线性无关,则向最组在,豆7的秩为 (较易) 37.设向量组a=(L,2,3),4=(2,10),么,=(5,a,5)的铁为2,则数a- 一(中等) 38,设刀阶矩阵A的各行元素之和均为0,且A的秩为刀-1,则齐次线性方程组Ax■0的 解为 (难) 4起 39.设4,4,是齐次线性方程组在=0的两个解,则A24+584) (较易)】 0,设A是刚×n矩韩,其秩为(<),则齐次线性方程组Ax=0的基础解系所含解向量的 个数为 个.(较易》 41,齐次线性方程组 +-x3+x4-2x=0 的基础解系所含解向量的个数为 2写+2高2-2第+2x+高=0 (较易) 写=5+名■0 2,齐次线性方程组 的基础解系为 (中等) +3+3红=0 3.设A是m×开矩库,则齐次线性方程组AX=0有无穷多解的充要条件是 ,。(中等) 三、解答题 44.下列向量组中的向量B能否由其余向量线性表示,如能求其表达式:
32.设三阶矩阵 1 0 0 2 2 0 3 3 3 A = 则矩阵 A 的秩为 .(较易) 33.设三阶矩阵 1 1 3 1 2 5 339 A = 则矩阵 A 的秩为 .(较易) 34.设三阶矩阵 1 2 3 2 3 5 3 4 7 A = 则矩阵 A 的秩为 .(较易) 35.设 1 2 1 2 2 2 1 6 1 0 3 A t − = − − ,已知 R A( ) 2 = ,则 t = (中等) 36.已知向量组向量 , , 线性相关,而 , , 线性无关,则向量组 , , 的秩为 (较易) 37.设向量组 1 2 3 = = = (1,2,3 , 2,1,0 , 5, ,5 ) ( ) ( a ) uur uur uur 的秩为 2,则数 a = .(中等) 38.设 n 阶矩阵 A 的各行元素之和均为 0,且 A 的秩为 n−1 ,则齐次线性方程组 Ax = 0 的 解为 (难) 39.设 1 uur ,2 uur 是齐次线性方程组 Ax = 0 的两个解,则 A(2 1 2 + 5 ) uur uur = .(较易) 40.设 A 是 m n 矩阵,其秩为 r n ( ) ,则齐次线性方程组 Ax = 0 r r 的基础解系所含解向量的 个数为 个.(较易) 41.齐次线性方程组 1 2 3 4 5 1 2 3 4 5 2 0 2 2 2 2 0 x x x x x x x x x x + − + − = + − + + = 的基础解系所含解向量的个数为 (较易) 42.齐次线性方程组 1 2 3 1 2 3 0 3 0 x x x x x x − + = + + = 的基础解系为 .(中等) 43.设 A 是 mn 矩阵,则齐次线性方程组 AX = 0 有无穷多解的充要条件是 .(中等) 三、解答题 44.下列向量组中的向量 能否由其余向量线性表示,如能求其表达式

2 1)a, ,3 -3 10 3 (2) 2 1 1 1 1 0 0 (3) 0 3 0 0 45.投向量组a=(6,+1,3,C=(2.-2),二,=(依,1.0),试问k为何值时,么4,4 线性相关?真为何值时,线性无关?(较难) 48设a,BX,乃,乃均为4维列向量,A=(@,,乃,乃,B=(B,X,乃,方)为4阶方库,若 行列式IA上4|B卜1,求行列式|A+B1的值。(中等) 47,判断下列向量组的线性相关性《中等) 2 1 0 1 (1)a 6 12 (2)= 2 ,03= 3 3 5 10 5 6 0 2 2 1 0 3 2 2 -1 0 (3)■ 2 (4) 3 2 4: 7 3 2 2 2 14 8.求下列各向量组的秩和一个极大无关组,并用该极大无关组表示其余向量。《较难) 9 2 1 4 (1)4= 1 1 2 4 4 -8 2 (2 2 3 5 (2)4,= 3 -4 a,= 8 a= -9 a -3 -12 2
(1) 1 2 3 1 1 1 2 = 1 , = 2 , = 0 , = 3 ; 1 0 3 7 − − (2) 1 ,2 3 4 1 1 1 1 1 1 1 1 1 2 = = = = , = ; 1 1 1 1 1 1 1 1 1 1 − − − − − − , , , (3) 1 ,2 3 4 1 2 1 0 0 1 1 1 1 0 = = = = , = . 0 3 0 1 0 1 1 0 1 1 − − , , , 45.设向量组 1 2 3 (6, 1,3 , ,2, 2 , ,1,0 ) ( ) ( ) T T T = + = − = k k k uur uur uur ,试问 k 为何值时, 1 2 3 ,,, 线性相关? k 为何值时,线性无关?(较难) 46.设 1 2 3 , , , , 均为 4 维列向量, 1 2 3 1 2 3 A B = = ( , , , ), ( , , , ) 为 4 阶方阵,若 行列式 | | 4,| | 1 A B = = ,求行列式 | | A B + 的值。(中等) 47.判断下列向量组的线性相关性(中等) (1) 1 2 3 2 3 6 = 1 = 6 , = 12 3 5 10 − , ; (2) 1 2 3 1 0 1 = 1 = 2 , = 3 1 5 6 , ; (3) 1 ,2 3 4 0 2 1 2 1 2 2 1 = = = = 2 3 1 1 3 1 2 2 − − − , , , ; (4) 1 ,2 3 1 0 3 1 3 0 = = = . 2 1 7 4 2 14 − , , 48.求下列各向量组的秩和一个极大无关组,并用该极大无关组表示其余向量.(较难) (1) 1 1 2 = 1 4 − , 2 9 1 = 1 4 , 3 2 4 = 2 8 − − − ; (2) 1 2 3 1 2 2 2 3 5 = = = 3 4 8 4 1 3 − − − − , , , 4 5 5 3 26 4 = = 9 1 12 2 − − − , ;

11 2 0 0 1 0 (3)41= a3= a= a,= 0 1 0 0 0 1 1 0 3 -1 3 0 -I (4)a1 2 d:= a1= C,日 5 a= 2 14 6 0 1 1 0 1 2 -1 2 1 3 6 (5)a1 0 a,= 1 a 4 0 -1 9.求下列线性方程组的通解(中等) x-名+2x1-x=0 名+名-5x=0 2x+%+3x+7x=6 (0) 元+2x3+2x,=0 (2) 2无+馬2-3x4=0 (3)3x+2%+2x+5x=4 2%-马+7%+x=0 属+馬-高+2x,=0 9%+73+%+4x=2 四、应用慰 50.有甲,乙、丙三种化肥,甲种化肥每千克含氨70克,顾8克,钾2克:乙种化肥每千克 含氯64克,磷0克,钾1克:丙件化肥每千克含氮0克,磷2克,甲3克:若某植物需 要氨1580克,磷149克,钾30克,则三种化配各需多少千克? 51.一家服装厂共有三个加工车间.第一车间用1匹布能产产4件村农15条长解和3件外农: 第二车间用1匹布能生产4件村农5条长裤和9件外农:第三车间用1瓜布隆生产8件村衣 10条长辨和3件外衣。现该厂接到一张订单,要求供应2000件村衣3500条长裤和2400件 外农.问该厂应如何向3个车间安排加工任务,以完成该订单?(难) 52,一个饮食专家计划一份替食,提供一定量的推生素C、钙和镁。其中用到3种食物,它 们的质量用适当的单位计量,这些食品提侯的营养以及食带需要的营养知下表给出 表1营养食调问题 单位食谱所含的营养(毫克) 营养 需要的营养总量(意克) A食物 B食物 C食物 维生素C 10 20 20 100 钙 50 40 10 300 镁 30 10 200 针对这个问题写出一个向量方程。说明方程中的变量表示什么?然后求解这个方程
(3) 1 1 0 1 0 = , 2 1 1 0 0 = , 3 2 1 1 0 = , 4 0 0 1 1 = . (4) 1 2 3 1 0 3 1 3 0 = = = 2 1 7 4 2 14 − , , , 4 5 2 1 1 1 = = 5 2 6 0 − , ; (5) 1 2 3 1 1 0 1 2 1 = = = 0 1 1 0 1 1 − − − , , , 4 5 1 2 3 6 = = 2 4 1 1 − , ; 49.求下列线性方程组的通解(中等) 1 2 3 4 234 1 2 3 4 2 0 (1) 2 2 0 2 7 0 x x x x x x x x x x x − + − = + + = − + + = 1 3 4 1 2 4 1 2 3 4 5 0 (2) 2 3 0 2 0 x x x x x x x x x x + − = + − = + − + = 1 2 3 4 1 2 3 4 1 2 3 4 2 3 7 6 (3) 3 2 2 5 4 9 7 4 2 x x x x x x x x x x x x + + + = + + + = + + + = 四、应用题 50.有甲、乙、丙三种化肥,甲种化肥每千克含氮 70 克,磷 8 克,钾 2 克;乙种化肥每千克 含氮 64 克,磷 10 克,钾 1 克;丙种化肥每千克含氮 70 克,磷 12 克,钾 3 克;若某植物需 要氮 1580 克,磷 149 克,钾 30 克,则三种化肥各需多少千克? 51.一家服装厂共有三个加工车间。第一车间用 1 匹布能产产 4 件衬衣 15 条长裤和 3 件外衣; 第二车间用 1 匹布能生产 4 件衬衣 5 条长裤和 9 件外衣;第三车间用 1 匹布能生产 8 件衬衣 10 条长裤和 3 件外衣。现该厂接到一张订单,要求供应 2000 件衬衣 3500 条长裤和 2400 件 外衣.问该厂应如何向 3 个车间安排加工任务,以完成该订单?(难) 52.一个饮食专家计划一份膳食,提供一定量的维生素 C、钙和镁。其中用到 3 种食物,它 们的质量用适当的单位计量。这些食品提供的营养以及食谱需要的营养如下表给出 表 1 营养食谱问题 营养 单位食谱所含的营养(毫克) 需要的营养总量(毫克) A 食物 B 食物 C 食物 维生素 C 10 20 20 100 钙 50 40 10 300 镁 30 10 40 200 针对这个问题写出一个向量方程。说明方程中的变量表示什么?然后求解这个方程
53.设某中药厂用六种中草药(AE)根据不同的比例配制了三种特效药(1-3号),各成份 用量如下表《单位:克)现在该医院想用这四件特效药再配制二种新的特效药(45号), 这三种新的特效药的成分也在下表中,月能否配制?如何配置? 1号成药 2号成药 3号成药 4号成药 5号成药 A 5 12 19 31 B 1 6 14 22 36 5 25 60 0 36 D 3 15 38 58 97 E2 11 25 41 67
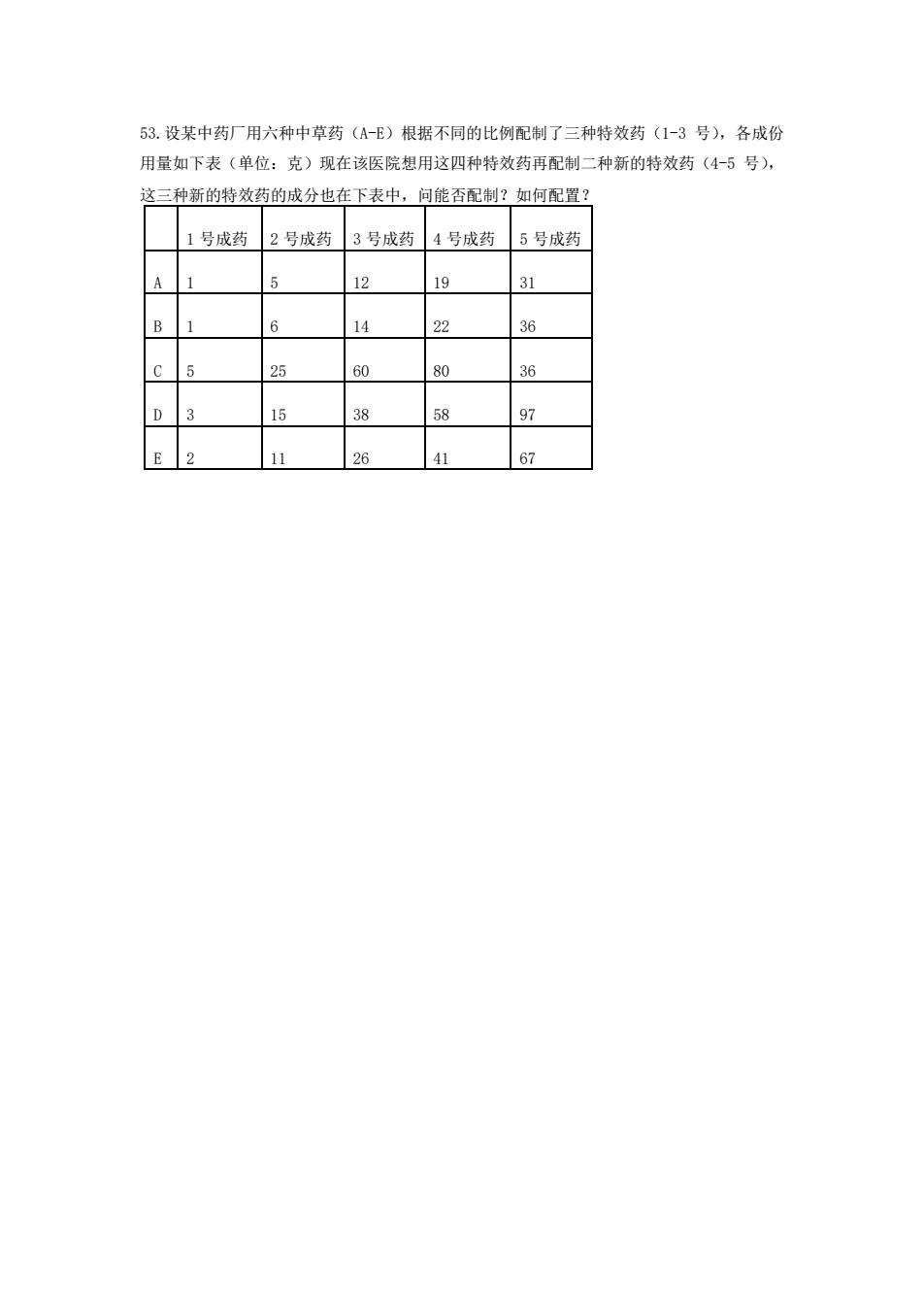
53.设某中药厂用六种中草药(A-E)根据不同的比例配制了三种特效药(1-3 号),各成份 用量如下表(单位:克)现在该医院想用这四种特效药再配制二种新的特效药(4-5 号), 这三种新的特效药的成分也在下表中,问能否配制?如何配置? 1 号成药 2 号成药 3 号成药 4 号成药 5 号成药 A 1 5 12 19 31 B 1 6 14 22 36 C 5 25 60 80 36 D 3 15 38 58 97 E 2 11 26 41 67