
第四章数字特征 一、选择愿 1、(易)设随机变量X的概率密度为f八= 2x0≤xg 其他 则E(X)-( B C.I 00 2.(中等)设X为随机变量:A2,DN5,则A42-() A4 B.9 C.13 D21 3,(哥)设随机变量X-偶LP),且EX)=24.优X)=14,则参数m,P的值分别为) A4和0.6 B.6和04 C.8和03 D3和0.s 4、(中等)设随机变量X与了不相关,则以下结论中排误的是) A.E(+Y)-E(X)+E(Y) BDYX+Y)-D000+D(V) C.E)-E0E/) D.DOY)-D(XDYY) 5、(哥)设随机变量X一N(以,a),Y服从参数为从元>0)的指数分布,则下列结论中不正 确的是() AEX-D=H-元 Br-n=-克 C.EX=4,Em=元 D.DX0=G2D=元 6、(中等)设随机变量X与了相互独立,且X,Y分别服从参数为1,4的泊松分布,则 DX-)( A-3 B.-1 C.3 D.5 7、(中等)设随机变量X服从参数为3的泊松分布,了一B8,),且X。Y相互独立 则DX-3Y-4)=() A.13 B.15 C.19 D.23
1 第四章 数字特征 一、选择题 1、(易)设随机变量 X 的概率密度为 = 0, , 2 , 0 1; ( ) 其他 x x f x 则 E X( ) = ( ) A. 3 1 B. 3 2 C.1 D. 3 10 2、(中等)设 X 为随机变量,E(X)=2,D(X)=5,则 E(X+2)2=( ) A.4 B.9 C.13 D.21 3、(易)设随机变量 X B n p ~ ( , ) ,且 E X D X ( ) 2.4, ( ) 1.44 = = ,则参数 n,p 的值分别为( ) A. 4 和 0.6 B.6 和 0.4 C. 8 和 0.3 D.3 和 0.8 4、(中等)设随机变量 X 与 Y 不相关,则以下结论中错误..的是( ) A.E(X+Y)=E(X)+E(Y) B.D(X+Y)=D(X)+D(Y) C. E(XY)=E(X)E(Y) D.D(XY)=D(X)D(Y) 5、(易)设随机变量 2 X N~ ( , ) ,Y 服从参数为 ( 0) 的指数分布,则下列结论中不正.. 确.的是( ) A. 1 E X Y ( ) − = − B. 2 2 1 D X Y ( ) − = − C. 1 E X E Y ( ) , ( ) = = D. 2 2 1 D X D Y ( ) , ( ) = = 6、(中等)设随机变量 X 与 Y 相互独立,且 X,Y 分别服从参数为 1,4 的泊松分布,则 D(X-Y)= ( ) A.-3 B.-1 C.3 D.5 7、(中等)设随机变量 X 服从参数为 3 的泊松分布, 1 (8, ) 3 Y B ,且 X,Y 相互独立, 则 D X Y ( 3 4) − − =( ) A.-13 B.15 C.19 D.23

星 8、(中等)设随机变量X的概率密度为八)■ 2x7e .则E).D0分别为() A.-35 B.-3.2 C.3.2 D.32 9、(中等)设二推随机变量(KN(1,2:2,3护:).则水-Y() A.N-3-5) B.N-313) C.N(1,) D.N(I,13) 10、(中等)已知D0-1,D(-25,Px=04,则DX) A.6 B.30 C.22 D.46 1、(葛)设二推随机变量X门N(4,,a,o:P):且X与Y相互独立,则p=() A.-1 B.0 C.I D.2 12、(牧)设随机变景X-B00,,Y-N2,10,又E)=14.则X与y的相 关系数P=() A.-0.8 B.-0.16 C.01 D.08 13、(中等)授随机变量X的方差DW存在,且D0>0,令Y=-X,则Pm=() A.-1 B.0 C.1 D2 二、填空题 14、(悬)设随机变量的分布律为PX=:=1/5,k=1,2,34,5,则E(X)”一 15、(中等)设随机变量X~U(-1.3),则D2X-3引= 16、(岛)设随机变量X-B18,,则DX。 3 EX) 17、《中等)设随机变量X服从参数为0.5的指数分布,则 18、(易》设随机变量X与Y找性不相关,则C州X-2,Y+1)= 2
2 8、(中等)设随机变量 X 的概率密度为 4 ( 3) 2 e 2π 2 1 ( ) + − = x f x , 则 E (X), D (X)分别为 ( ) A. − 3, 2 B.-3, 2 C.3, 2 D.3, 2 9、 (中等)设二维随机变量 (X, Y)~N (-1, -2;2 2 , 32 ;0), 则 X-Y~ ( ) A.N (-3, -5) B.N (-3,13) C.N (1, 13 ) D.N (1,13) 10、(中等)已知 D(X)=1,D(Y)=25, 0.4 XY = ,则 D(X-Y)=( ) A.6 B.30 C.22 D.46 11、(易)设二维随机变量(X,Y)~N 2 2 1 2 1 2 ( , ; , ; ) ,且 X 与 Y 相互独立,则 =( ) A.-1 B.0 C. 1 D.2 12、(较难)设随机变量 1 (10, ) 2 X B ,Y N(2,10) ,又 E XY ( ) 14 = ,则 X 与 Y 的相 关系数 XY = ( ) A.-0.8 B.-0.16 C.0.1 D.0.8 13、 (中等)设随机变量 X 的方差 D(X)存在,且 D(X)>0,令 Y X = − ,则 XY = ( ) A. −1 B.0 C. 1 D.2 二、填空题 14、(易)设随机变量 X 的分布律为 P X k k { } 1/ 5, 1,2,3,4,5 = = = , 则 E X( ) =________. 15、(中等)设随机变量 X U( 1,3) − ,则 D X (2 3) − =_________. 16、(易)设随机变量 1 (18, ) 3 X B ,则 = E(X) D(X) ____________. 17、(中等)设随机变量 X 服从参数为 0.5 的指数分布,则 E(X 2 )=______. 18、(易)设随机变量 X 与 Y 线性不相关,则 Cov X Y ( 2, 1) − + =____________
19、(易)设随机变量X与了的协方差CoMA.Y-1则Co2Y,-3X)一 20、(较难)设二维随机变量X,门的分布律 y -1 025 0.25 025 025 则E+ 21、(希)设二推随机变量(化,D的概率密度为xy m,x>0.y20.则Pm=一 0. 其他 三、计算恩 22、(中等)设随机变量X的分布律为妇 X 2 0 3 P 0.3 0.403 记Y=X,求:(1)DX),E):(2)Cow(4K.Y) 23、(较难)二维随机变量(X,门的分布律 -1 0 0 0.3 02 0.1 0.1 0.3 0 求:(1)4X-)1 ()Cov(X.Y). 24、(中等)设随机变量X的展率密度为 x 0sx<1 f(x)2-x Isx<2 0 其他 Y-2+l,求:()E0,En(2)DD 25、(中等)已知随机变量X的密度函数为 ar2+bx+c,0≤xs1 f(x)= 0 其他 又已知E05,D015,求a,b,c 3
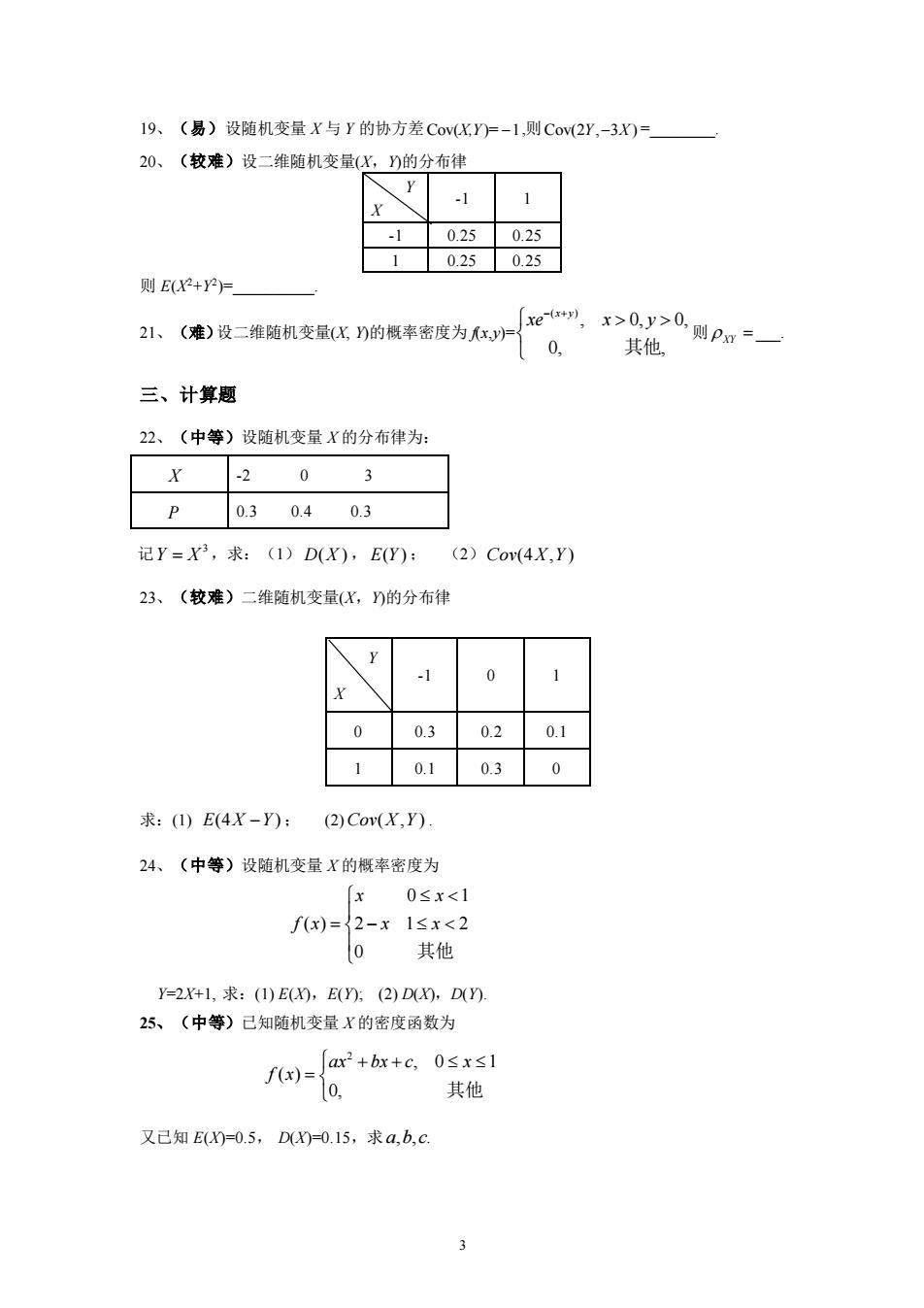
3 19、(易)设随机变量 X 与 Y 的协方差 Cov( )= 1 X,Y − ,则 Cov(2 , 3 ) Y X − =________. 20、(较难)设二维随机变量(X,Y)的分布律 Y X -1 1 -1 0.25 0.25 1 0.25 0.25 则 E(X 2+Y 2 )=__________. 21、(难)设二维随机变量(X, Y)的概率密度为 f(x,y)= ( ), 0, 0, 0, , x y xe x y − + 其他 则 XY = ___. 三、计算题 22、(中等)设随机变量 X 的分布律为: X -2 0 3 P 0.3 0.4 0.3 记 3 Y X = ,求:(1) D X( ) , E Y( ) ; (2) Cov X Y (4 , ) 23、(较难)二维随机变量(X,Y)的分布律 求:(1) E X Y (4 ) − ; (2) Cov X Y ( , ) . 24、(中等)设随机变量 X 的概率密度为 0 1 ( ) 2 1 2 0 x x f x x x = − 其他 Y=2X+1, 求:(1) E(X),E(Y); (2) D(X),D(Y). 25、(中等)已知随机变量 X 的密度函数为 2 , 0 1 ( ) 0, ax bx c x f x + + = 其他 又已知 E(X)=0.5, D(X)=0.15,求 abc , , . Y X -1 0 1 0 0.3 0.2 0.1 1 0.1 0.3 0

26、(难)设水,Y是相互魏立的面机变量,其概率密度分别为 2x.0sx≤1. f(x)= e-.y>5. 0, 其他 ()= 0 其他 求E(Y) 27、(中等)设随机变量K,Y的顺率密度分别为 「2e,x>0, f(x)- (v)■ [4ey,y>0 lo. x≤0 0. ys0. 求:()EX+Y),(2)E2X+3r) 四、应用题 28、(中等)袋中有12个零件。其中9个合格品,3个废品.安装机器时,从袋中一个一个 地取出(取出后不放回),设在取出合格品之前已取出的废品数为随机变量X,求E(X) 和D(X) 29、(较难)一工厂生产某种没备的寿命X(以年计)服从指数分布,概率密度为 x>0 o. x≤0 为确保清费者的利益。工厂规定出售的设备若在一年内损坏可以调换若售出一台设备,工 厂获利100元,面调换一台则损失200元,试求工厂出售一台设备赢利的数学期里
4 26、(难)设 X,Y 是相互独立的随机变量,其概率密度分别为 2 , 0 1, ( ) 0, ; X x x f x = 其他 ( 5) e , 5, ( ) 0, . y Y y f y − − = 其他 求 E XY ( ). 27、(中等)设随机变量 X,Y 的概率密度分别为 2 2 , 0, ( ) 0, 0; x X e x f x x − = 4 4 , 0, ( ) 0, 0. y Y e y f y y − = 求:(1) E X Y ( ) + ; (2) 2 E X Y (2 3 ) + . 四、应用题 28、(中等)袋中有 12 个零件,其中 9 个合格品,3 个废品.安装机器时,从袋中一个一个 地取出(取出后不放回),设在取出合格品之前已取出的废品数为随机变量 X,求 E(X) 和 D(X). 29、(较难)一工厂生产某种设备的寿命 X(以年计)服从指数分布,概率密度为 f(x)= − 0, 0. , 0, 4 1 4 x x x e 为确保消费者的利益,工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备,工 厂获利 100 元,而调换一台则损失 200 元,试求工厂出售一台设备赢利的数学期望