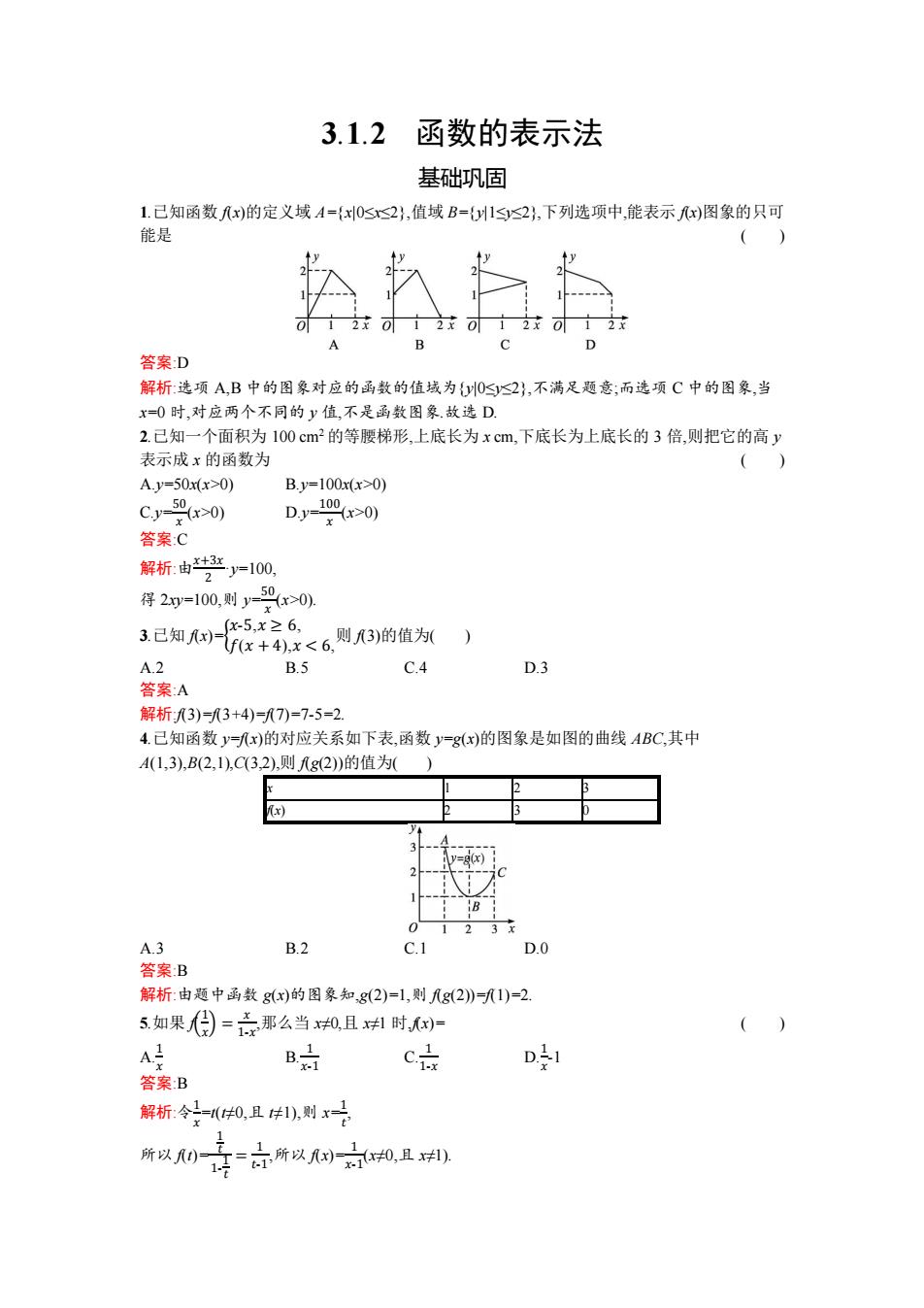
3.1.2 函数的表示法 基础巩固 1.已知函数x)的定义域A={x0s2,值域B={1s0) B.y=100x(x>0) Cy-0 Dy90y 答案:C 解析:由+ 2100 得2=10,则y2>0 3.已知x)= x-5,x≥6, f(x+4),x<6, 则3)的值为( A.2 B.5 C.4 D.3 答案:A 解析3)=3+4)=7)=7-5=2. 4.已知函数y=x)的对应关系如下表,函数y=g(x)的图象是如图的曲线ABC,其中 A(1,3),B(2,1),C(3,2),则g2)的值为( 2 r) A.3 B.2 C.1 D.0 答案B 解析:由题中函数gx)的图象知,g(2)=1,则g2)=1)=2 5如果得=总那么当0且对时) A里 B时 c品 D 答案:B 解析:今40,且1),则x 听以0主行所以心点0卫中
3.1.2 函数的表示法 基础巩固 1.已知函数 f(x)的定义域 A={x|0≤x≤2},值域 B={y|1≤y≤2},下列选项中,能表示 f(x)图象的只可 能是 ( ) 答案:D 解析:选项 A,B 中的图象对应的函数的值域为{y|0≤y≤2},不满足题意;而选项 C 中的图象,当 x=0 时,对应两个不同的 y 值,不是函数图象.故选 D. 2.已知一个面积为 100 cm2 的等腰梯形,上底长为 x cm,下底长为上底长的 3 倍,则把它的高 y 表示成 x 的函数为 ( ) A.y=50x(x>0) B.y=100x(x>0) C.y= 50 𝑥 (x>0) D.y= 100 𝑥 (x>0) 答案:C 解析:由 𝑥+3𝑥 2 ·y=100, 得 2xy=100,则 y= 50 𝑥 (x>0). 3.已知 f(x)={ 𝑥-5,𝑥 ≥ 6, 𝑓(𝑥 + 4),𝑥 < 6, 则 f(3)的值为( ) A.2 B.5 C.4 D.3 答案:A 解析:f(3)=f(3+4)=f(7)=7-5=2. 4.已知函数 y=f(x)的对应关系如下表,函数 y=g(x)的图象是如图的曲线 ABC,其中 A(1,3),B(2,1),C(3,2),则 f(g(2))的值为( ) x 1 2 3 f(x) 2 3 0 A.3 B.2 C.1 D.0 答案:B 解析:由题中函数 g(x)的图象知,g(2)=1,则 f(g(2))=f(1)=2. 5.如果 f( 1 𝑥 ) = 𝑥 1-𝑥 ,那么当 x≠0,且 x≠1 时,f(x)= ( ) A.1 𝑥 B. 1 𝑥-1 C. 1 1-𝑥 D.1 𝑥 -1 答案:B 解析:令 1 𝑥 =t(t≠0,且 t≠1),则 x= 1 𝑡 , 所以 f(t)= 1 𝑡 1- 1 𝑡 = 1 𝑡-1 ,所以 f(x)= 1 𝑥-1 (x≠0,且 x≠1)

6.某航空公司规定,乘客所携带行李的质量(单位:kg)与其运费(单位:元)由图中的函数图象确 定则乘客可免费携带行李的最大质量为() ↑y元 930 630 330 304050x/kg A.50 kg B.30kg C.19kg D.40 kg 答案C 解析:由题图可知,函数的图象是一条直线,可以用一次函数表示,设为y=kc+b(k0),将点 (30,330),(40,630)的坐标分别代入可求得k=30,b=-570,则y=30x-570,令y=0,得x=19. 7.己知函数x)的图象如图所示,则函数x)的解析式为 牛 以 可1234x 2x,0≤x≤1, 答案x)=2,11, 9.己知函数x)= 0x2+1,-1≤x≤1, 2x+3,x1,-2》=2=1+号= ②)当a>1时人@=1日=是解得a=2>1,符合题意: 当-1sa1时,a)=+1是 解得a=受l,特合题意 当a<1时,@)=2a+3三解得a=子1,不符合题意。 综上4=2或a=号 10.已知函数x)=x2+r+n(m,n∈R),术0)=1),且方程x=x)有两个相等的实数根
6.某航空公司规定,乘客所携带行李的质量(单位:kg)与其运费(单位:元)由图中的函数图象确 定,则乘客可免费携带行李的最大质量为( ) A.50 kg B.30 kg C.19 kg D.40 kg 答案:C 解析:由题图可知,函数的图象是一条直线,可以用一次函数表示,设为 y=kx+b(k≠0),将点 (30,330),(40,630)的坐标分别代入可求得 k=30,b=-570,则 y=30x-570,令 y=0,得 x=19. 7.已知函数 f(x)的图象如图所示,则函数 f(x)的解析式为 . 答案:f(x)={ 2𝑥,0 ≤ 𝑥 ≤ 1, 2,1 1, 𝑥 2 + 1,-1 ≤ 𝑥 ≤ 1, 2𝑥 + 3,𝑥 1,∴f(f(f(-2)))=f(2)=1+ 1 2 = 3 2 . (2)当 a>1 时,f(a)=1+ 1 𝑎 = 3 2 ,解得 a=2>1,符合题意; 当-1≤a≤1 时,f(a)=a2+1= 3 2 , 解得 a=± √2 2 ∈[-1,1],符合题意; 当 a-1,不符合题意. 综上,a=2 或 a=± √2 2 . 10.已知函数 f(x)=x2+mx+n(m,n∈R),f(0)=f(1),且方程 x=f(x)有两个相等的实数根

(1)求函数x)的解析式: (2)当x∈[0,3]时,求函数x)的值域 解(1)x)=x2+x+n,且0)=1), ∴.n=l+m+n. ∴m=-1. ∴jx)=x2-x+n. ,方程x=x)有两个相等的实数根,即方程x2-2x+n=0有两个相等的实数根,∴.△=(-2)2-4n-0, 解得n=1.x)=x2-x+1 (2)由(1),知x)=x2-x+1. 此函数图象的开口向上,对称轴为直线x号 ·当x之时x)有最小值,最小值为) 而⑤=()-1=0=13)=323+1=7, “当x∈0,3]时,函数x)的值城是居,7 拓展提高 1.己知函数g()=1.06×(0.75[+1),其中>0,0为1的整数部分,则g5.5)=() A.5.035 B.5.56 C.5.84 D.5.38 答案:A 解析g5.5)=1.06×(0.75×5+1)=5.035 2.定义两种运算:a⊕b=Va2-b2,c⑧b= @b则函数)2票的解折式 A=x∈-2,0U(0,21 Bx区x∈(,-2U2,to) CE(2JUB2.) D.e20u02 答案D 解析:由已知得2⊕r=V4-x2x⑧2=(x-2)2 )2x V4-xZ (x@2)-2 √x-2)2.2 4-x2≥0, (-2≤x≤2, Nx-2)2-2≠0, 得 x≠0,且x≠4, ∴.-2≤r<0或0<x2 即定义域为[-2,0)U(0,2] )区 22-.xx∈-2,0)U(0,21故选D 3.作出下列函数的图象: (1y=x2.4x (2y=x2-4x (3)y=x2.4x 解(1)函数y=x2.4x的图象如图①所示
(1)求函数 f(x)的解析式; (2)当 x∈[0,3]时,求函数 f(x)的值域. 解:(1)∵f(x)=x2+mx+n,且 f(0)=f(1), ∴n=1+m+n. ∴m=-1. ∴f(x)=x2 -x+n. ∵方程 x=f(x)有两个相等的实数根,即方程 x 2 -2x+n=0 有两个相等的实数根,∴Δ=(-2)2 -4n=0, 解得 n=1.∴f(x)=x2 -x+1. (2)由(1),知 f(x)=x2 -x+1. 此函数图象的开口向上,对称轴为直线 x= 1 2 . ∴当 x= 1 2时,f(x)有最小值,最小值为 f( 1 2 ). 而 f( 1 2 ) = ( 1 2 ) 2 − 1 2 +1= 3 4 ,f(0)=1,f(3)=3 2 -3+1=7, ∴当 x∈[0,3]时,函数 f(x)的值域是[ 3 4 ,7]. 拓展提高 1.已知函数 g(t)=1.06×(0.75[t]+1),其中 t>0,[t]为 t 的整数部分,则 g(5.5)=( ) A.5.035 B.5.56 C.5.84 D.5.38 答案:A 解析:g(5.5)=1.06×(0.75×5+1)=5.035. 2.定义两种运算:a⊕b=√𝑎 2-𝑏 2,a b=√(𝑎-𝑏) 2 ,则函数 f(x)= 2⊕𝑥 (𝑥⊗2)-2的解析式为( ) A.f(x)= √4-𝑥 2 𝑥 ,x∈[-2,0)∪(0,2] B.f(x)= √4-𝑥 2 𝑥 ,x∈(-∞,-2]∪[2,+∞) C.f(x)=- √4-𝑥 2 𝑥 ,x∈(-∞,-2]∪[2,+∞) D.f(x)=- √4-𝑥 2 𝑥 ,x∈[-2,0)∪(0,2] 答案:D 解析:由已知得 2⊕x=√4-𝑥 2,x 2=√(𝑥-2) 2 , ∴f(x)= 2⊕𝑥 (𝑥⊗2)-2 = √4-𝑥 2 √(𝑥-2) 2 -2 . 由{ 4-𝑥 2 ≥ 0, √(𝑥-2) 2 -2 ≠ 0, 得{ -2 ≤ 𝑥 ≤ 2, 𝑥 ≠ 0,且𝑥 ≠ 4, ∴-2≤x<0 或 0<x≤2, 即定义域为[-2,0)∪(0,2]. ∴f(x)= √4-𝑥 2 2-𝑥-2 =- √4-𝑥 2 𝑥 ,x∈[-2,0)∪(0,2].故选 D. 3.作出下列函数的图象: (1)y=x2 -4x; (2)y=x2 -4|x|; (3)y=|x2 -4x|. 解:(1)函数 y=x2 -4x 的图象如图①所示
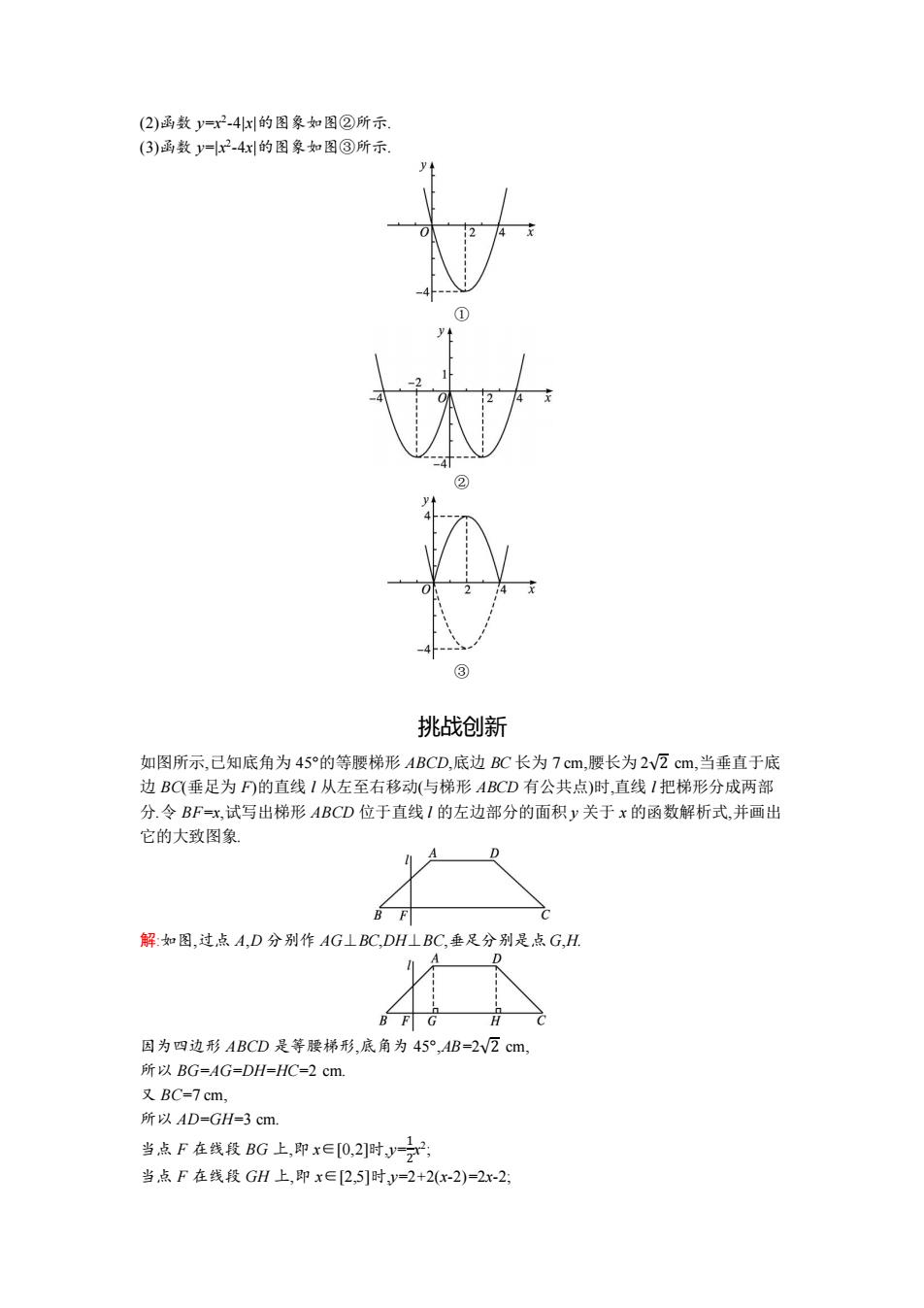
(2)函数y=x2-4x的图象如图②所示 (3)函数y=x2-4x的图象如图③所示. ③ 挑战创新 如图所示,己知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2VZcm,当垂直于底 边BC(垂足为F的直线I从左至右移动(与梯形ABCD有公共点)时,直线I把梯形分成两部 分.令BF=x,试写出梯形ABCD位于直线I的左边部分的面积y关于x的函数解析式,并画出 它的大致图象 B 解:如图,过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是点G,H A B FG 因为四边形ABCD是等腰梯形,底角为45°,AB-2V2cm, 所以BG=AG=DH=HC=2cm. 又BC=7cm, 所以AD=GH=3cm. 当点F在线段BG上,即x∈0,2]时之 当点F在线段GH上,即x∈[2,5]时y=2+2(x-2)=2x-2
(2)函数 y=x2 -4|x|的图象如图②所示. (3)函数 y=|x2 -4x|的图象如图③所示. ① ② ③ 挑战创新 如图所示,已知底角为 45°的等腰梯形 ABCD,底边 BC 长为 7 cm,腰长为 2√2 cm,当垂直于底 边 BC(垂足为 F)的直线 l 从左至右移动(与梯形 ABCD 有公共点)时,直线 l 把梯形分成两部 分.令 BF=x,试写出梯形 ABCD 位于直线 l 的左边部分的面积 y 关于 x 的函数解析式,并画出 它的大致图象. 解:如图,过点 A,D 分别作 AG⊥BC,DH⊥BC,垂足分别是点 G,H. 因为四边形 ABCD 是等腰梯形,底角为 45°,AB=2√2 cm, 所以 BG=AG=DH=HC=2 cm. 又 BC=7 cm, 所以 AD=GH=3 cm. 当点 F 在线段 BG 上,即 x∈[0,2]时,y= 1 2 x 2 ; 当点 F 在线段 GH 上,即 x∈[2,5]时,y=2+2(x-2)=2x-2;
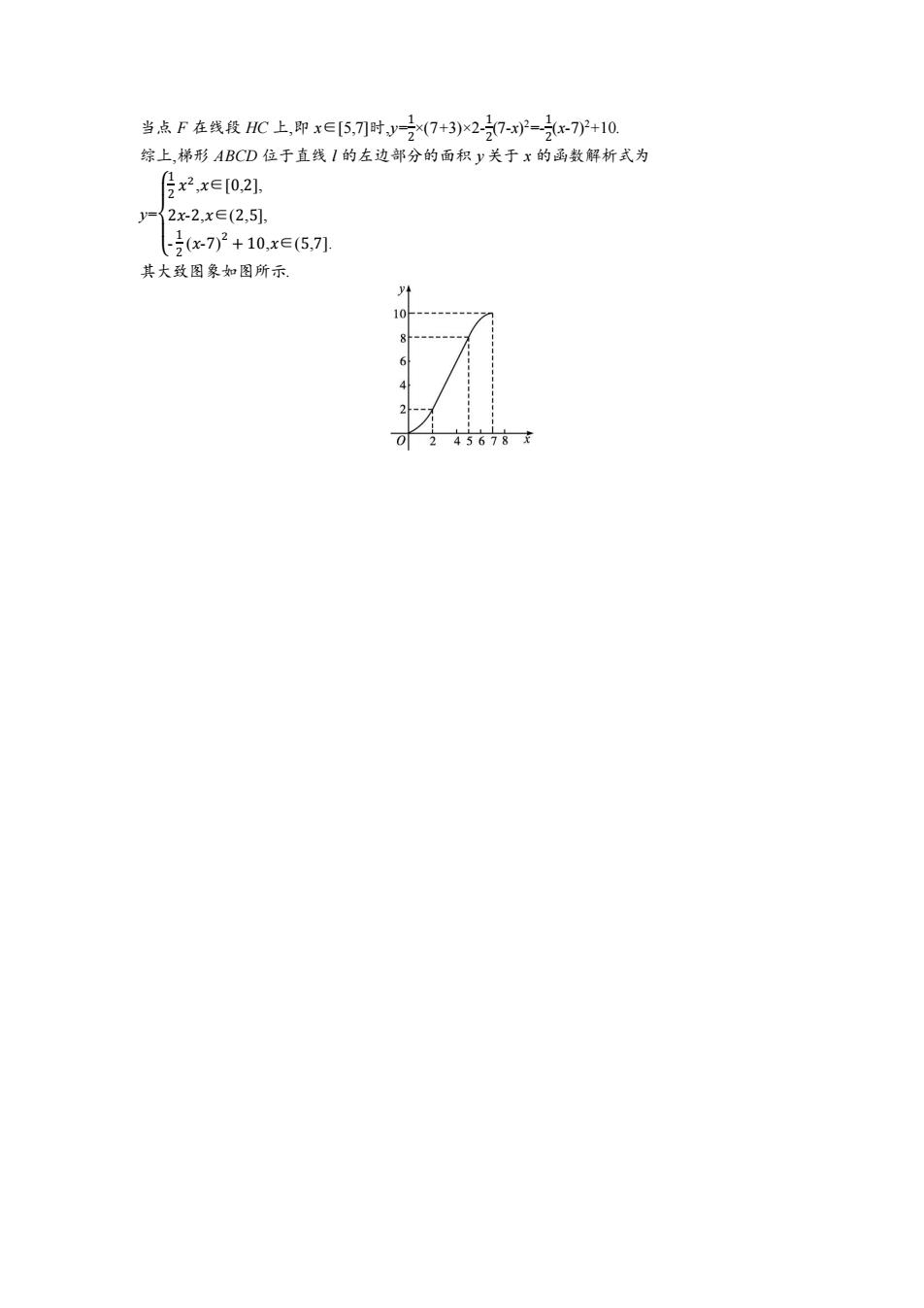
当点F在线段HC上,即x∈[5,7刀时,y之(7+3)×2-27-x2-2x-7+10. 综上,梯形ABCD位于直线I的左边部分的面积y关于x的函数解析式为 月x2,x∈0,21. y=2x-2,x∈(2,5], 2x-7)2+10,x∈(5,7刀 其大致图象如图所示 6 4 0245678末
当点 F 在线段 HC 上,即 x∈[5,7]时,y= 1 2 ×(7+3)×2- 1 2 (7-x) 2=- 1 2 (x-7)2+10. 综上,梯形 ABCD 位于直线 l 的左边部分的面积 y 关于 x 的函数解析式为 y= { 1 2 𝑥 2 ,𝑥∈[0,2], 2𝑥-2,𝑥∈(2,5], - 1 2 (𝑥-7) 2 + 10,𝑥∈(5,7]. 其大致图象如图所示