5.4三角函数的图象与性质 5.4.1 正弦函数、余弦函数的图象 基础巩固 1.用“五点法”作函数y=2six1的图象时,首先应描出的五点的横坐标可以是() A0,5r2 B.0票 C.0,π,2π,3π,4π D.0唱是9 答案:A 解析:由“五,点法”可知选A 2.方程sinx品的根的个数是( A.7 B.8 C.9 D.10 答案:A 解析在同一平面直角坐标系内作出六和)一snx的图象,知图所示 y =0 4π-3 根据图象可知,方程有7个根 3.函数y=sinx 0sina成立的a的取值范围为 () A(琴) B.(0,) C(0,)u(π-)D(m-)u(任) 答案:A
5.4 三角函数的图象与性质 5.4.1 正弦函数、余弦函数的图象 基础巩固 1.用“五点法”作函数 y=2sin x-1 的图象时,首先应描出的五点的横坐标可以是( ) A.0,π 2 ,π, 3π 2 ,2π B.0,π 4 , π 2 , 3π 4 ,π C.0,π,2π,3π,4π D.0,π 6 , π 3 , π 2 , 2π 3 答案:A 解析:由“五点法”可知选 A. 2.方程 sin x= 𝑥 10的根的个数是( ) A.7 B.8 C.9 D.10 答案:A 解析:在同一平面直角坐标系内作出 y= 𝑥 10和 y=sin x 的图象,如图所示. 根据图象可知,方程有 7 个根. 3.函数 y=sin x·| cos𝑥 sin𝑥 |(0sin α 成立的 α 的取值范围为 ( ) A.(- 3π 4 , π 4 ) B.(0, π 4 ) C.(0, π 4 ) ∪ (-π,- 3π 4 ) D.(-π,- 3π 4 ) ∪ ( π 4 ,π) 答案:A
解析:画出y=sin x.y=cosx的图象如图所示,由图象可知在区间(-元,)内使cosa>sina成立的 a的取值范国是(平》 =C0S2 6.若sinx=2m+1,且x∈R,则m的取值范围是 答案[1,0] 解析:sinx∈[-l,l] ∴.-1≤2m+1≤1,故-1≤ms0. 7.己知y=sinx和y=cosx的图象的三个连续的交点A,B,C构成△ABC,则△ABC的面积等 于 答案√Zπ 解析:由正弦函数、余弦函数的图象(图略)可得y=six和y=cosx的图象的三个连续的交点 A,B,C构成的△ABC是等腰三角形,且易知底边长等于2π,高为VZ, 故△ABC的面积为2x2π×√2=2元 8已知函数网-件206则不等式网的解集是- 答案{x<x<0或君+2km<x<+2kmk∈N 解析在同一平面直角坐标系中作出函数)的图象和直线y之图略),由图易得x<0或 吾+2a<rg+2ka,keN 9.用“五点法”作出函数y=2sinx,x∈[0,2π的简图. 解列表: 3π 2元 2sinx 0 0 描点、连线,如图所示 2 10根据)=0sx的图象解不等式c0s字x∈0,2 解:函数y=cosx,x∈[0,2π的图象如图所示 2π 根据图象可得,不等式的解集为{x侣≤x≤兽或 g≤x≤别 6 拓展提高
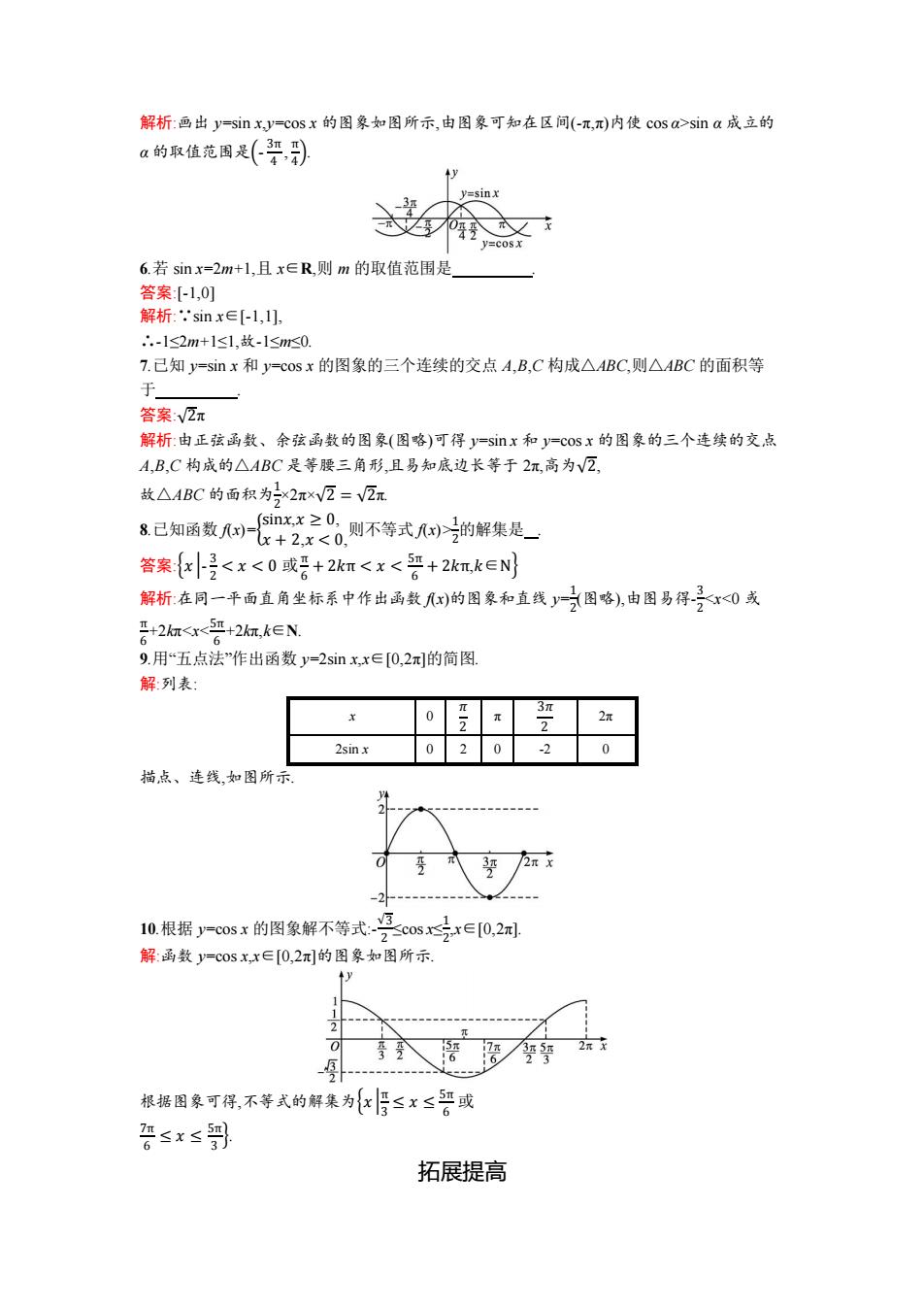
解析:画出 y=sin x,y=cos x 的图象如图所示,由图象可知在区间(-π,π)内使 cos α>sin α 成立的 α 的取值范围是(- 3π 4 , π 4 ). 6.若 sin x=2m+1,且 x∈R,则 m 的取值范围是 . 答案:[-1,0] 解析:∵sin x∈[-1,1], ∴-1≤2m+1≤1,故-1≤m≤0. 7.已知 y=sin x 和 y=cos x 的图象的三个连续的交点 A,B,C 构成△ABC,则△ABC 的面积等 于 . 答案:√2π 解析:由正弦函数、余弦函数的图象(图略)可得 y=sin x 和 y=cos x 的图象的三个连续的交点 A,B,C 构成的△ABC 是等腰三角形,且易知底边长等于 2π,高为√2, 故△ABC 的面积为1 2 ×2π×√2 = √2π. 8.已知函数 f(x)={ sin𝑥,𝑥 ≥ 0, 𝑥 + 2,𝑥 1 2 的解集是 . 答案:{𝑥 |- 3 2 < 𝑥 < 0 或 π 6 + 2𝑘π < 𝑥 < 5π 6 + 2𝑘π,𝑘∈N} 解析:在同一平面直角坐标系中作出函数 f(x)的图象和直线 y= 1 2 (图略),由图易得- 3 2 <x<0 或 π 6 +2kπ<x<5π 6 +2kπ,k∈N. 9.用“五点法”作出函数 y=2sin x,x∈[0,2π]的简图. 解:列表: x 0 𝜋 2 π 3𝜋 2 2π 2sin x 0 2 0 -2 0 描点、连线,如图所示. 10.根据 y=cos x 的图象解不等式:- √3 2 ≤cos x≤ 1 2 ,x∈[0,2π]. 解:函数 y=cos x,x∈[0,2π]的图象如图所示. 根据图象可得,不等式的解集为{𝑥 | π 3 ≤ 𝑥 ≤ 5π 6 或 7π 6 ≤ 𝑥 ≤ 5π 3 }. 拓展提高

1.函数y=-xcOsx的部分图象是( 答案D 解析:y=-xCOS x是奇函数,其图象关于原点对称 ∴排除A,C项;当xe(0,)时,y=-osx<0, 排除B项 故选D 2(多选题)关于函数x)=l+cosx,x∈(传,2m的图象与直线y=1为常数)的交点情况,下列说 法正确的是 () A.当<0或仑2时,有0个交点 B当10或1<2时,有1个交点 C当0<时,有2个交点 D.当0<1<2时,有2个交点 答案:AB 解析:画出函数x)的图象如图所示 π 3梦2r末 对于选项A,当1<0或仑2时,有0个交点,故A中说法正确对于选项B,当1=0或<2时,有 1个交点,故B中说法正确对于选项C,当1时,只有1个交点,故C中说法错误对于选项D, 当1<2时,只有1个交点,故D中说法错误 3.有下列结论: ①y=sinx的图象与y=sinx的图象关于y轴对称; ②y=cos(-x)的图象与y=cosx的图象相同; ③y=|sinx的图象与y=sin(-x)的图象关于x轴对称; ④y=cosx的图象与y=cos(-x)的图象相同. 其中正确的是 (填序号)。 答案:②④ 解析:对于②,y=C0s(-x)=cosx,y=cosx=cosx,故其图象相同: 对于④,y=c0s(-x)=c0sx,故这两个函数的图象相同,作图(图略)可知①③均不正确. 4.函数y=cosx+4,x∈[0,2π]的图象与直线y=4的交点的坐标为 答案任4)(4) 解析由化三C0sx+4得cosK0, y=4 当x∈0,2可时,x我x受 “文点为侣4)(受4 5.用五点法”作出函数y=1-2sinx,x∈[-元,π的简图,并回答下列问题: (1)观察函数图象,写出满足下列条件的x的取值范围
1.函数 y=-xcos x 的部分图象是( ) 答案:D 解析:∵y=-xcos x 是奇函数,其图象关于原点对称, ∴排除 A,C 项;当 x∈(0, π 2 )时,y=-xcos x<0, ∴排除 B 项. 故选 D. 2.(多选题)关于函数 f(x)=1+cos x,x∈( π 3 ,2π)的图象与直线 y=t(t 为常数)的交点情况,下列说 法正确的是 ( ) A.当 t<0 或 t≥2 时,有 0 个交点 B.当 t=0 或 3 2 ≤t<2 时,有 1 个交点 C.当 0<t≤ 3 2时,有 2 个交点 D.当 0<t<2 时,有 2 个交点 答案:AB 解析:画出函数 f(x)的图象如图所示. 对于选项 A,当 t<0 或 t≥2 时,有 0 个交点,故 A 中说法正确.对于选项 B,当 t=0 或 3 2 ≤t<2 时,有 1 个交点,故 B 中说法正确.对于选项 C,当 t= 3 2 时,只有 1 个交点,故 C 中说法错误.对于选项 D, 当 3 2 ≤t<2 时,只有 1 个交点,故 D 中说法错误. 3.有下列结论: ①y=sin|x|的图象与 y=sin x 的图象关于 y 轴对称; ②y=cos(-x)的图象与 y=cos|x|的图象相同; ③y=|sin x|的图象与 y=sin(-x)的图象关于 x 轴对称; ④y=cos x 的图象与 y=cos(-x)的图象相同. 其中正确的是 (填序号). 答案:②④ 解析:对于②,y=cos(-x)=cos x,y=cos|x|=cos x,故其图象相同; 对于④,y=cos(-x)=cos x,故这两个函数的图象相同,作图(图略)可知①③均不正确. 4.函数 y=cos x+4,x∈[0,2π]的图象与直线 y=4 的交点的坐标为 . 答案:( π 2 ,4), ( 3π 2 ,4) 解析:由{ 𝑦 = cos𝑥 + 4, 𝑦 = 4, 得 cos x=0, 当 x∈[0,2π]时,x= π 2或 x= 3π 2 . ∴交点为( π 2 ,4), ( 3π 2 ,4). 5.用“五点法”作出函数 y=1-2sin x,x∈[-π,π]的简图,并回答下列问题: (1)观察函数图象,写出满足下列条件的 x 的取值范围

①y>1;②y1. (2)若直线y=a与y=1-2sinx,x∈[-元,π的图象有两个交点,求实数a的取值范围. 解:列表如下: x -元 sinx 1-2sinx 描点并将它们用光滑的曲线连接起来,如图: y -延O y=1-2 sinxxE[-π,r] (1)由图象可知,图象在直线y=1上方部分时y>1,在直线y=1下方部分时y1;②当x∈(0,π)时y1. (2)如图所示,当直线y=a与y=l-2sinx,x∈[-元,π的图象有两个交点时,1<a<3或-1<a<1,所以 实数a的取值范围是(-1,1)U(1,3) 挑战创新 若方程sinx在区间店,上有两个实数根,求a的取值范围, 解在同一平面直角坐标系中作出snxx∈侣的图象,直线y空知图所示 y=sinx 由图象可知,当号s兴1,即-1c13时,inx∈售,小的圈象与直线)兰有两个文点 即方程snx学在区同唱止有两个实数根 故a的取值范围为(-1,1-V3
①y>1;②y1,在直线 y=1 下方部分时 y1;②当 x∈(0,π)时,y<1. (2)如图所示,当直线 y=a 与 y=1-2sin x,x∈[-π,π]的图象有两个交点时,1<a<3 或-1<a<1,所以 实数 a 的取值范围是(-1,1)∪(1,3). 挑战创新 若方程 sin x= 1-𝑎 2 在区间[ π 3 ,π]上有两个实数根,求 a 的取值范围. 解:在同一平面直角坐标系中作出 y=sin x,x∈[ π 3 ,π]的图象,直线 y= 1-𝑎 2 ,如图所示. 由图象可知,当 √3 2 ≤ 1-𝑎 2 <1,即-1<a≤1-√3时,y=sin x,x∈[ π 3 ,π]的图象与直线 y= 1-𝑎 2 有两个交点, 即方程 sin x= 1-𝑎 2 在区间[ π 3 ,π]上有两个实数根. 故 a 的取值范围为(-1,1-√3]