6.2.1向量的加法运算 课后·训练提升 基础巩固 1.(多选题)下列各式中一定成立的是() A.a+b=b+a B.0+a=a C.AC +CB=AB D.la+b|=a+b 答案ABC 解桐因为A,B,C项满足运算律及运算法则,所以一定成立.而D项不一定成立,因为 |a+b≤a+bl,只有当a,b同向时等号才成立 2.对于任意一个四边形ABCD,下列式子不能化简为BC的是(). A.BA+AD +DC B.BD+DA+AC C.AB+BD DC D.DC BA+AD 嗒案c 解桐在A中,BA+AD+DC=BD+DC=BC;在B中,BD+DA+AC=BA+AC=BC;在 C中,AB+BD+DC=AD+DC=AC,在D中,DC+BA+AD=DC+BD=BD+D元= BC. 3.如图,在正六边形ABCDEF中,BA+CD+EF等于( ) A.0 B.BE C.AD D.CF 答案D 解析BA+CD+EF=DE+CD+EF=CE+EF=CF 4.(AB+MB)+B0+B元)+OM等于(). A.BC B.AB C.AC D.AM 答案 解析原式=AB+ME+B0+BC+OM-(AB+BC)+(ME+BG+OM)=AC+0=AC 5.已知平行四边形ABCD,设AB+CD+BC+DA=a,且b是一非零向量,则下列结论:①a∥b: ②a+b=a;③a+b=b;④a+b<a+lbl.其中正确的是( ) A.①③ B.②③ C.②④ D.①② 答案A 解析:在平行四边形ABCD中,AB+C而0,BC+DA-0,:a为零向量,:“零向量和任意向量 都平行,零向量和任意向量的和等于这个向量本身,:①③中的结论正确,②④中的结论错误」 6.在平行四边形ABCD中,若BC+BA=BC+AEL,则四边形ABCD是 答案矩形 解析:1BC+BA=BD,BC+AB=AC1,且BC+BA=BC+AB1,:BD1=AC1 又四边形ABCD是平行四边形, ,:四边形ABCD是矩形
6.2.1 向量的加法运算 课后· 基础巩固 1.(多选题)下列各式中一定成立的是( ). A.a+b=b+a B.0+a=a C.𝐴𝐶⃗⃗ + 𝐶𝐵⃗⃗⃗ = 𝐴𝐵⃗⃗⃗ D.|a+b|=|a|+|b| 答案 ABC 解析因为 A,B,C 项满足运算律及运算法则,所以一定成立.而 D 项不一定成立,因为 |a+b|≤|a|+|b|,只有当 a,b 同向时等号才成立. 2.对于任意一个四边形 ABCD,下列式子不能化简为𝐵𝐶⃗⃗⃗ 的是( ). A.𝐵𝐴⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ + 𝐷𝐶⃗⃗⃗ B.𝐵𝐷⃗ ⃗ + 𝐷𝐴⃗⃗⃗⃗ + 𝐴𝐶⃗⃗ C.𝐴𝐵⃗⃗⃗ + 𝐵𝐷⃗ ⃗ + 𝐷𝐶⃗⃗⃗ D.𝐷𝐶⃗⃗⃗ + 𝐵𝐴⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ 答案 C 解析在 A 中,𝐵𝐴⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ + 𝐷𝐶⃗⃗⃗ = 𝐵𝐷⃗ ⃗ + 𝐷𝐶⃗⃗⃗ = 𝐵𝐶⃗⃗⃗ ;在 B 中,𝐵𝐷⃗ ⃗ + 𝐷𝐴⃗⃗⃗⃗ + 𝐴𝐶⃗⃗ = 𝐵𝐴⃗⃗⃗ + 𝐴𝐶⃗⃗ = 𝐵𝐶⃗⃗⃗ ;在 C 中,𝐴𝐵⃗⃗⃗ + 𝐵𝐷⃗ ⃗ + 𝐷𝐶⃗⃗⃗ = 𝐴𝐷⃗⃗⃗⃗ + 𝐷𝐶⃗⃗⃗ = 𝐴𝐶⃗⃗ ;在 D 中,𝐷𝐶⃗⃗⃗ + 𝐵𝐴⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ = 𝐷𝐶⃗⃗⃗ + 𝐵𝐷⃗ ⃗ = 𝐵𝐷⃗ ⃗ + 𝐷𝐶⃗⃗⃗ = 𝐵𝐶⃗⃗⃗ . 3.如图,在正六边形 ABCDEF 中,𝐵𝐴⃗⃗⃗ + 𝐶𝐷⃗⃗⃗ + 𝐸𝐹⃗⃗ 等于( ). A.0 B.𝐵𝐸⃗⃗⃗ C.𝐴𝐷⃗⃗⃗⃗ D.𝐶𝐹⃗⃗ 答案 D 解析𝐵𝐴⃗⃗⃗ + 𝐶𝐷⃗⃗⃗ + 𝐸𝐹⃗⃗ = 𝐷𝐸⃗⃗⃗⃗ + 𝐶𝐷⃗⃗⃗ + 𝐸𝐹⃗⃗ = 𝐶𝐸⃗⃗ + 𝐸𝐹⃗⃗ = 𝐶𝐹⃗⃗ . 4.(𝐴𝐵⃗⃗⃗ + 𝑀𝐵 ⃗⃗⃗⃗ )+(𝐵𝑂⃗⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ )+𝑂𝑀⃗⃗⃗⃗ 等于( ). A.𝐵𝐶⃗⃗⃗ B.𝐴𝐵⃗⃗⃗ C.𝐴𝐶⃗⃗ D.𝐴𝑀⃗⃗⃗⃗ 答案 C 解析原式=𝐴𝐵⃗⃗⃗ + 𝑀𝐵 ⃗⃗⃗⃗ + 𝐵𝑂⃗⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ + 𝑂𝑀⃗⃗⃗⃗ =(𝐴𝐵⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ )+(𝑀𝐵 ⃗⃗⃗⃗ + 𝐵𝑂⃗⃗⃗⃗ + 𝑂𝑀⃗⃗⃗⃗ )=𝐴𝐶⃗⃗ +0=𝐴𝐶⃗⃗ . 5.已知平行四边形 ABCD,设𝐴𝐵⃗⃗⃗ + 𝐶𝐷⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ + 𝐷𝐴⃗⃗⃗⃗ =a,且 b 是一非零向量,则下列结论:①a∥b; ②a+b=a;③a+b=b;④|a+b|<|a|+|b|.其中正确的是( ). A.①③ B.②③ C.②④ D.①② 答案 A 解析∵在平行四边形 ABCD 中,𝐴𝐵⃗⃗⃗ + 𝐶𝐷⃗⃗⃗ =0,𝐵𝐶⃗⃗⃗ + 𝐷𝐴⃗⃗⃗⃗ =0,∴a 为零向量,∵零向量和任意向量 都平行,零向量和任意向量的和等于这个向量本身,∴①③中的结论正确,②④中的结论错误. 6.在平行四边形 ABCD 中,若|𝐵𝐶⃗⃗⃗ + 𝐵𝐴⃗⃗⃗ |=|𝐵𝐶⃗⃗⃗ + 𝐴𝐵⃗⃗⃗ |,则四边形 ABCD 是 . 答案矩形 解析∵|𝐵𝐶⃗⃗⃗ + 𝐵𝐴⃗⃗⃗ |=|𝐵𝐷⃗ ⃗ |,|𝐵𝐶⃗⃗⃗ + 𝐴𝐵⃗⃗⃗ |=|𝐴𝐶⃗⃗ |,且|𝐵𝐶⃗⃗⃗ + 𝐵𝐴⃗⃗⃗ |=|𝐵𝐶⃗⃗⃗ + 𝐴𝐵⃗⃗⃗ |,∴|𝐵𝐷⃗ ⃗ |=|𝐴𝐶⃗⃗ |. 又四边形 ABCD 是平行四边形, ∴四边形 ABCD 是矩形

7.如图所示,若点P为△ABC的外心,且PA+P元=P元,则∠ACB= 答案120 解析因为PA+PB=PC,所以四边形APBC是平行四边形.因为点P为△4BC的外心,所以 PA=PB=PC.所以四边形PACB是菱形,且△PAC与△PBC是全等的等边三角形.所以∠ ACB=120° 8.已知在菱形ABCD中,∠DAB=60°,AB=1,则BC+CD1=」 答案 解析在△ABD中,AD=AB=1,∠DAB=60°, 则BD=1,则BC+CD1=BD=1. 9.己知正方形ABCD的边长为1,AB=a,AC=b,BC=c,则|a+b+c= 答案22 解桐因为正方形ABCD的边长为1,所以AC=VZ,所以a+b+c=AB+AC+BC1=AE+BC+ ACI=AC ACI=2ACI=2V2. 10.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,P为平面内任意一点 求证:PA+PB+P元+PD=4P0. 证明:P☑+P電+PC+P⑦=P0+0i+P0+0死+P0+0C+P0+0而=4P0+(OA+ 0元+0元+0D)=4P0+(0A+0元)+(0元+0D)=4P0+0+0=4P0, .:PA+PB+P元+PD=4P0 11.如图(1)(2),已知向量a,b,c,求作向量a+b和a+b+c. a (1) (2) 解1)作法:在平面内任取一点0,作0A-a,A正=b,则O丽=a+b. (2)在平面内任意取一点O,作0元=b,BC=c,CA=a,则0A=a+b+c
7.如图所示,若点 P 为△ABC 的外心,且𝑃𝐴⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ = 𝑃𝐶⃗⃗ ,则∠ACB= . 答案 120° 解析因为𝑃𝐴⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ = 𝑃𝐶⃗⃗ ,所以四边形 APBC 是平行四边形.因为点 P 为△ABC 的外心,所以 PA=PB=PC.所以四边形 PACB 是菱形,且△PAC 与△PBC 是全等的等边三角形.所以∠ ACB=120°. 8.已知在菱形 ABCD 中,∠DAB=60°,|𝐴𝐵⃗⃗⃗ |=1,则|𝐵𝐶⃗⃗⃗ + 𝐶𝐷⃗⃗⃗ |= . 答案 1 解析在△ABD 中,AD=AB=1,∠DAB=60°, 则 BD=1,则|𝐵𝐶⃗⃗⃗ + 𝐶𝐷⃗⃗⃗ |=|𝐵𝐷⃗ ⃗ |=1. 9.已知正方形 ABCD 的边长为 1,𝐴𝐵⃗⃗⃗ =a,𝐴𝐶⃗⃗ =b,𝐵𝐶⃗⃗⃗ =c,则|a+b+c|= . 答案 2√2 解析因为正方形 ABCD 的边长为 1,所以 AC=√2,所以|a+b+c|=|𝐴𝐵⃗⃗⃗ + 𝐴𝐶⃗⃗ + 𝐵𝐶⃗⃗⃗ |=|𝐴𝐵⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ + 𝐴𝐶⃗⃗ |=|𝐴𝐶⃗⃗ + 𝐴𝐶⃗⃗ |=2|𝐴𝐶⃗⃗ |=2√2. 10.如图,在平行四边形 ABCD 中,对角线 AC 与 BD 相交于点 O,P 为平面内任意一点. 求证:𝑃𝐴⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ + 𝑃𝐶⃗⃗ + 𝑃𝐷⃗⃗⃗ =4𝑃𝑂⃗⃗⃗ . 证明∵𝑃𝐴⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ + 𝑃𝐶⃗⃗ + 𝑃𝐷⃗⃗⃗ = 𝑃𝑂⃗⃗⃗ + 𝑂𝐴⃗⃗⃗ + 𝑃𝑂⃗⃗⃗ + 𝑂𝐵⃗⃗⃗⃗ + 𝑃𝑂⃗⃗⃗ +⃗𝑂𝐶⃗⃗ + 𝑃𝑂⃗⃗⃗ + 𝑂𝐷⃗⃗ =4𝑃𝑂⃗⃗⃗ +(𝑂𝐴⃗⃗⃗ + 𝑂𝐵⃗⃗⃗⃗ + ⃗𝑂𝐶⃗⃗ + 𝑂𝐷⃗⃗ )=4𝑃𝑂⃗⃗⃗ +(𝑂𝐴⃗⃗⃗ +⃗𝑂𝐶⃗⃗ )+(𝑂𝐵⃗⃗⃗⃗ + 𝑂𝐷⃗⃗ )=4𝑃𝑂⃗⃗⃗ +0+0=4𝑃𝑂⃗⃗⃗ , ∴𝑃𝐴⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ + 𝑃𝐶⃗⃗ + 𝑃𝐷⃗⃗⃗ =4𝑃𝑂⃗⃗⃗ . 11.如图(1)(2),已知向量 a,b,c,求作向量 a+b 和 a+b+c. 解(1)作法:在平面内任取一点 O,作𝑂𝐴⃗⃗⃗ =a,𝐴𝐵⃗⃗⃗ =b,则𝑂𝐵⃗⃗⃗⃗ =a+b. (2)在平面内任意取一点 O,作𝑂𝐵⃗⃗⃗⃗ =b,𝐵𝐶⃗⃗⃗ =c,𝐶𝐴⃗⃗ =a,则𝑂𝐴⃗⃗⃗ =a+b+c

拓展提高 1.(多选题)向量a,b均为非零向量,下列说法中正确的是(). A.若向量a与b反向,且a>b,则向量a+b的方向与a的方向相同 B.若向量a与b反向,且a<bl,则向量a+b的方向与a的方向相同 C.若向量a与b同向,则向量a+b的方向与a的方向相同 D.若向量a与b同向,则向量a+b的方向与b的方向相同 答案ACD 解析当向量a与b反向,且a<bl时,向量a+b的方向与b的方向相同,只有B项说法错 误,A,C,D项中的说法都正确. 2.(多选题)如图,D,E,F分别是△4BC的边AB,BC,CA的中点,则下列等式成立的是( A.FD+DA+DE-0 B.AD +BE CF=0 C.F⑦+DE+AD=AB D.AD+EC+FD=BD 答案ABC 懈析FD+DA+DE=FA+DE-0,故A中等式成立;AD+B配+CF=AD+DF+FA-0,故 B中等式成立;FD+DE+AD=FE+AD=AD+DE=AB,故C中等式成立,AD+EC+ 下FD=AD+0=AD=D元+BD,故D中等式不成立 3.若在△ABC中,AB=a,BC=b,且|a=b=1,a+b=√Z,则△4BC的形状是()片 A.等边三角形 B.锐角三角形 C钝角三角形 D.等腰直角三角形 答案D 解析因为AB=a=1,BC1=b-1,AC1=a+b=VZ,所以△4BC为等腰直角三角形.故选D. 4.己知△ABC的三个顶点A,B,C及平面内一点P,满足PA+P電=P乙,则下列结论正确的是 () A.点P在△ABC的内部 B.点P在△ABC的边AB上 C.点P在AB边所在的直线上 D.点P在△ABC的外部 客案D 解析P☑+PB=P元,根据平行四边形法则,如图所示,可知,点P在△ABC的外部. 5.已知点G是△4BC的重心,则GA+GE+GC= 答案 解析如图,延长AG交BC于点E,则点E为BC的中点,延长GE到点D,使GE=ED,则GE+ G元=GD,GD+GA=0,故GA+GB+G元-0
拓展提高 1.(多选题)向量 a,b 均为非零向量,下列说法中正确的是( ). A.若向量 a 与 b 反向,且|a|>|b|,则向量 a+b 的方向与 a 的方向相同 B.若向量 a 与 b 反向,且|a|<|b|,则向量 a+b 的方向与 a 的方向相同 C.若向量 a 与 b 同向,则向量 a+b 的方向与 a 的方向相同 D.若向量 a 与 b 同向,则向量 a+b 的方向与 b 的方向相同 答案 ACD 解析当向量 a 与 b 反向,且|a|<|b|时,向量 a+b 的方向与 b 的方向相同,只有 B 项说法错 误,A,C,D 项中的说法都正确. 2.(多选题)如图,D,E,F 分别是△ABC 的边 AB,BC,CA 的中点,则下列等式成立的是( ). A.𝐹𝐷⃗⃗⃗ + 𝐷𝐴⃗⃗⃗⃗ + 𝐷𝐸⃗⃗⃗⃗ =0 B.𝐴𝐷⃗⃗⃗⃗ + 𝐵𝐸⃗⃗⃗ + 𝐶𝐹⃗⃗ =0 C.𝐹⃗⃗⃗𝐷 + 𝐷𝐸⃗⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ = 𝐴𝐵⃗⃗⃗ D.𝐴𝐷⃗⃗⃗⃗ + 𝐸𝐶⃗⃗ + 𝐹𝐷⃗⃗⃗ = 𝐵𝐷⃗ ⃗ 答案 ABC 解析𝐹𝐷⃗⃗⃗ + 𝐷𝐴⃗⃗⃗⃗ + 𝐷𝐸⃗⃗⃗⃗ = 𝐹𝐴⃗⃗⃗ + 𝐷𝐸⃗⃗⃗⃗ =0,故 A 中等式成立;𝐴𝐷⃗⃗⃗⃗ + 𝐵𝐸⃗⃗⃗ + 𝐶𝐹⃗⃗ = 𝐴𝐷⃗⃗⃗⃗ + 𝐷𝐹⃗⃗⃗ + 𝐹𝐴⃗⃗⃗ =0,故 B 中等式成立;𝐹𝐷⃗⃗⃗ + 𝐷𝐸⃗⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ = 𝐹𝐸⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ = 𝐴𝐷⃗⃗⃗⃗ + 𝐷𝐵⃗ ⃗ = 𝐴𝐵⃗⃗⃗ ,故 C 中等式成立;𝐴𝐷⃗⃗⃗⃗ + 𝐸𝐶⃗⃗ + 𝐹𝐷⃗⃗⃗ = 𝐴𝐷⃗⃗⃗⃗ +0=𝐴𝐷⃗⃗⃗⃗ = 𝐷𝐵⃗ ⃗ ≠ 𝐵𝐷⃗ ⃗ ,故 D 中等式不成立. 3.若在△ABC 中,𝐴𝐵⃗⃗⃗ =a,𝐵𝐶⃗⃗⃗ =b,且|a|=|b|=1,|a+b|=√2,则△ABC 的形状是( ). A.等边三角形 B.锐角三角形 C.钝角三角形 D.等腰直角三角形 答案 D 解析因为|𝐴𝐵⃗⃗⃗ |=|a|=1,|𝐵𝐶⃗⃗⃗ |=|b|=1,|𝐴𝐶⃗⃗ |=|a+b|=√2,所以△ABC 为等腰直角三角形.故选 D. 4.已知△ABC 的三个顶点 A,B,C 及平面内一点 P,满足𝑃𝐴⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ = 𝑃𝐶⃗⃗ ,则下列结论正确的是 ( ). A.点 P 在△ABC 的内部 B.点 P 在△ABC 的边 AB 上 C.点 P 在 AB 边所在的直线上 D.点 P 在△ABC 的外部 答案 D 解析𝑃𝐴⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ = 𝑃𝐶⃗⃗ ,根据平行四边形法则,如图所示,可知点 P 在△ABC 的外部. 5.已知点 G 是△ABC 的重心,则𝐺𝐴⃗⃗⃗ + 𝐺𝐵⃗⃗⃗ + 𝐺𝐶⃗⃗ = . 答案 0 解析如图,延长 AG 交 BC 于点 E,则点 E 为 BC 的中点,延长 GE 到点 D,使 GE=ED,则𝐺𝐵⃗⃗⃗ + 𝐺𝐶⃗⃗ = 𝐺𝐷⃗⃗⃗⃗ ,𝐺𝐷⃗⃗⃗⃗ + 𝐺𝐴⃗⃗⃗ =0,故𝐺𝐴⃗⃗⃗ + 𝐺𝐵⃗⃗⃗ + 𝐺𝐶⃗⃗ =0
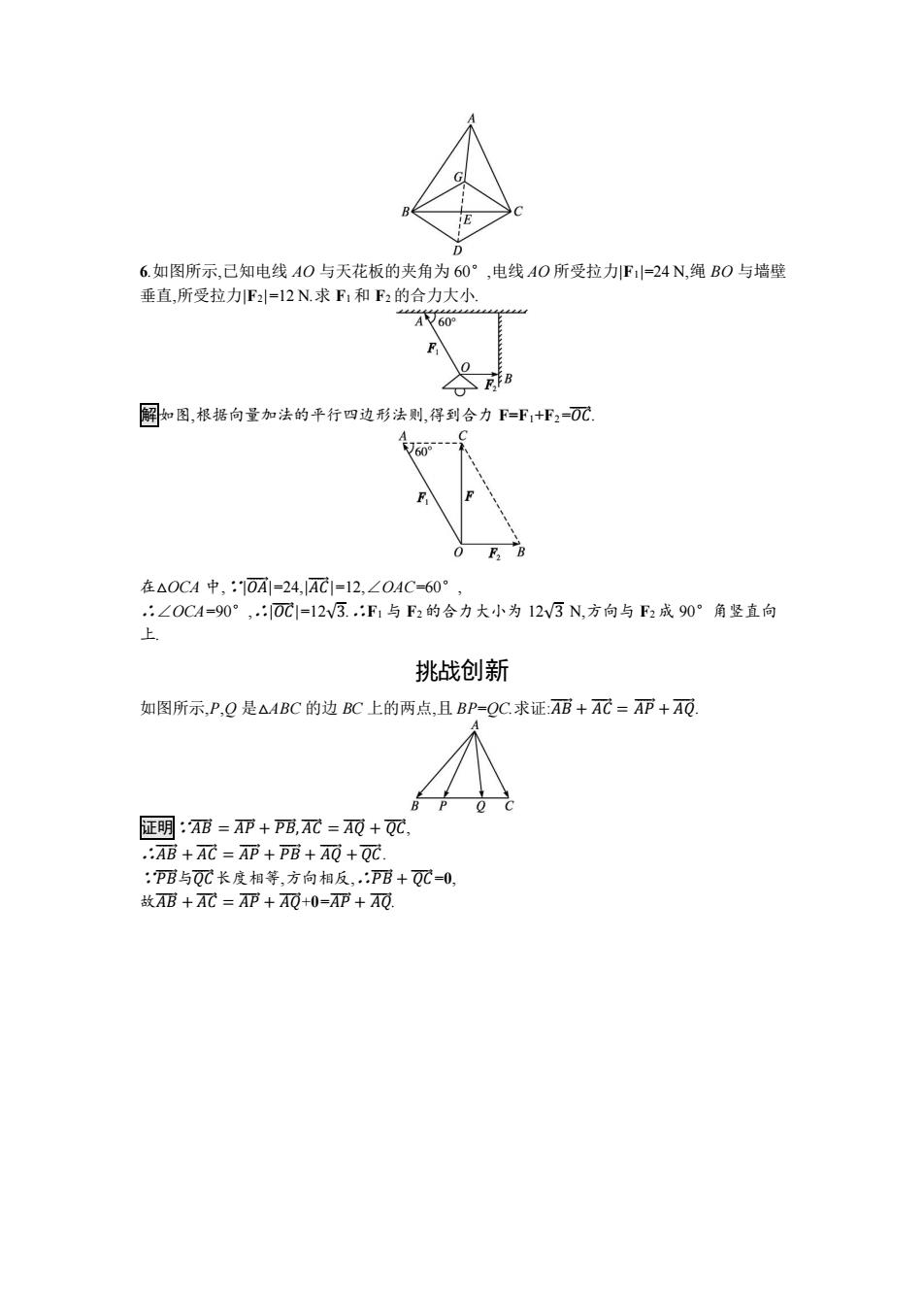
D 6.如图所示,已知电线AO与天花板的夹角为60°,电线AO所受拉力F1=24N,绳BO与墙壁 垂直,所受拉力F2=12N.求F,和F2的合力大小 “60 厨如图,根据向量加法的平行四边形法则,得到合力F-F+f2=0C 60° F,B 在△0CA中,:10A=24,AC1=12,∠OAC=60°, :∠OCA=90°,:0C1=12V3.:F1与F2的合力大小为12V3N,方向与F2成90°角竖直向 上. 挑战创新 如图所示,P,Q是△ABC的边BC上的两点,且BP-QC.求证:AE+AC=AP+AQ. 证明:正-亚+PB,AC-A0+QC, .:AB+AC=AP PB+AQ +QC :P呢与QC长度相等,方向相反,:PB+QC=0, AB +AC=AP+AQ+0=AP+AQ
6.如图所示,已知电线 AO 与天花板的夹角为 60°,电线 AO 所受拉力|F1|=24 N,绳 BO 与墙壁 垂直,所受拉力|F2|=12 N.求 F1 和 F2 的合力大小. 解如图,根据向量加法的平行四边形法则,得到合力 F=F1+F2=⃗𝑂𝐶⃗⃗ . 在△OCA 中,∵|𝑂𝐴⃗⃗⃗ |=24,|𝐴𝐶⃗⃗ |=12,∠OAC=60°, ∴∠OCA=90°,∴|⃗𝑂𝐶⃗⃗ |=12√3.∴F1 与 F2 的合力大小为 12√3 N,方向与 F2 成 90°角竖直向 上. 挑战创新 如图所示,P,Q 是△ABC 的边 BC 上的两点,且 BP=QC.求证:𝐴𝐵⃗⃗⃗ + 𝐴𝐶⃗⃗ = 𝐴𝑃⃗⃗⃗ + 𝐴𝑄⃗⃗⃗ . 证明∵𝐴𝐵⃗⃗⃗ = 𝐴𝑃⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ ,𝐴𝐶⃗⃗ = 𝐴𝑄⃗⃗⃗ + ⃗𝑄𝐶⃗⃗ , ∴𝐴𝐵⃗⃗⃗ + 𝐴𝐶⃗⃗ = 𝐴𝑃⃗⃗⃗ + 𝑃𝐵⃗⃗⃗ + 𝐴𝑄⃗⃗⃗ +⃗𝑄𝐶⃗⃗ . ∵𝑃𝐵⃗⃗⃗ 与⃗𝑄𝐶⃗⃗ 长度相等,方向相反,∴𝑃𝐵⃗⃗⃗ + ⃗𝑄𝐶⃗⃗ =0, 故𝐴𝐵⃗⃗⃗ + 𝐴𝐶⃗⃗ = 𝐴𝑃⃗⃗⃗ + 𝐴𝑄⃗⃗⃗ +0=𝐴𝑃⃗⃗⃗ + 𝐴𝑄⃗⃗⃗